众所周知，一个半群是次直积不可约的当且仅当其上存在最小非平凡同余.据文献[1]的推论Ⅵ.5.3，正规带簇中的次直积不可约成员只有5个，分别为L₂，R₂，Y₂，L₂⁰和R₂⁰.而在带簇的真子簇格中，几乎覆盖正规带簇的正则带簇，其次直积不可约成员有无限多个，且存在元素个数无限的次直积不可约正则带.所以，即使在正则带簇中，找遍所有互不同构的次直积不可约成员也是困难的.本文将找出元素个数不超过5的所有次直积不可约带.

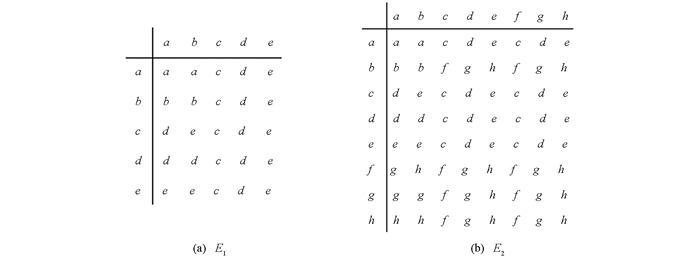
令X为非空集合，记ε_X为X上的相等关系，ω_X为X上的泛关系.令S为半群. S的对偶是指集合S上如下定义的运算∘所确定的半群：对任意a，b∈S，a∘b=ba，其中ba按半群S中的乘法作运算.通常记S的对偶半群为S^*.不难看出，半群S和S^*同时次直积不可约或同时次直积可约.文献[2]构造了以下两个非正则带，我们分别记其为E₁和E₂(图 1)：

并证明了：

引理1 带B是正则的当且仅当B中没有形如E₁，E₂，E₁^*和E₂^*的子带.

直接验证可得，ω_{b，c}∪ε_E1是E₁上的最小非平凡同余，因此，E₁是次直积不可约的^[3].不难看出，E₁的结构半格为Y₂.由引理1知，同构的意义下，元素个数不超过5的带除E₁和E₁^*外均是正则的.文中未介绍的术语符号及未提供证明的事实请读者参见文献[1, 4-5].

据文献[6]，有：

引理2 令S为半群.则S¹和S，S⁰和S均同时次直积不可约或同时次直积可约.

由文献[1]可知，任意正则带都是一左正则带和一右正则带的次直积.注意到，每一右正则带均是某左正则带的对偶.为研究次直积不可约的正则带，我们仅需研究次直积不可约的左正则带.令L为次直积不可约左正则带，据文献[5, 7]，L可记为[Y；L_α，ρ_α，β，φ_α，β].由文献[5]的引理1.3知，L的结构半格Y必含零元，记其为θ.据文献[5]，有以下两条引理：

引理3 对任意α∈Y-{θ}，有ρ_α，θ≠ω_Lθ.

引理4 对任意α∈Y，若ρ_α，θ=ε_Lθ，则$\left| {\mathop \cup \limits_{\delta \ge \alpha } L_\delta } \right| = 1$.

由文献[5]的定理2.16，我们可构造结构半格为Y₂的另一5元次直积不可约(左正则)带，记其为F，其乘法表如图 2：

引理5 对任意α∈Y-{θ}，ρ=ρ_α，θ∪ε_L是L上的同余.

证 易见ρ是L上的等价关系.又因L_θ是左零半群，为证ρ是L上的同余，只需证ρ左相容.任取(x，y)∈ρ，a∈L_β，则有ax=aφ_β，θ^x，ay=aφ_β，θ^y.当(x，y)∈ε_L时显然相容.现假设(x，y)∈ρ_α，θ.则ρ_α，θ∪ρ_β，θ ⊆ρ_αβ，θ.由关系映射的定义知

于是由文献[5]的引理1.5(ⅲ)知，对任意满足αβ≥γ的α，β，γ∈Y，a∈L_α，c∈L_γ，存在c′∈L_γ，使得

可得(ax，ay)∈ρ_α，θ.因此，ρ=ρ_α，θ∪ε_L是L上的同余.

下面给出本文的主要结论.

定理1 在同构的意义下，元素个数不大于5的次直积不可约带仅有以下13个：

证 据引理2及前述讨论，上列13个带均次直积不可约.由引理1知，同构的意义下，元素个数不大于5的非正则带仅有E₁和E₁^*.因此，我们仅需考虑正则的次直积不可约带，进而仅需考虑左正则的次直积不可约带.即证，元素个数不大于5的次直积不可约左正则带仅有以下6个：

注意到这6个带的结构半格均是链，据引理3和文献[5]的引理1.5，结构半格是链，不含零元，不含单位元且元素个数不大于5的次直积不可约左正则带仅有L₂和F.从而由引理2，结构半格是链且元素个数不大于5的次直积不可约左正则带仅有上述6个.因此，我们仅需证明不存在结构半格非链而元素个数不大于5的次直积不可约的左正则带.为此，令L=[Y；L_α，ρ_α，β，φ_α，β]为左正则次直积不可约带，θ为其结构半格Y的零元，且|L|≤5.若L只含3个元素，则L必为半格.据文献[1]，次直积不可约的半格仅有Y₂，因此不可能.以下分情况讨论：

情形1 |L|=4.

若L含零元，据引理2，L去掉零元后依然次直积不可约.因此，L去掉零元后所得带的结构半格依然不是链，据前述情形，也不可能.若L不含零元，则L只能有如图 3所示的半格分解：

由引理3和文献[5]的引理1.5(ⅲ)，这种情形也不可能.

情形2 |L|=5.

类似地，只可能有如图 4所示的4种半格分解：

又由引理3和文献[5]的引理1.5(ⅲ)，前3种分解依然不可能.关于第4种情形，假设d和e所在的L-类分别为L_α和L_β，由引理3和文献[5]的引理1.5(ⅲ)，ρ_α，θ和ρ_β，θ均既不是L_θ={a，b，c}上的泛关系也不是其上的相等关系.再据文献[5]的引理1.5(ⅲ)和关系映射的定义，ρ_α，θ和ρ_β，θ不同，从而由引理5知，L上存在两个非平凡同余ρ_α，θ∪ε_L和ρ_β，θ∪ε_L，它们的交为相等关系，这与L次直积不可约矛盾.

关于含元素个数更多的次直积不可约带，我们将结合逻辑推理与计算机编程的方法，进一步寻找.