-
近几十年以来,在分数阶微积分领域涌现出了求解分数阶微分方程[1-11]的一些有效方法,其中文献[10-11]提出了用变量分离法与齐次平衡原理以及积分分支法相结合的思想来求解时间分数阶非线性偏微分方程,这是一种新的求解思路,值得进一步跟踪研究.
目前,关于分数阶Klein-Gordon型方程精确解的研究[12-15]还比较少.因此,本文将利用文献[10-11]中关于变量分离法与齐次平衡原理相结合的思想,来研究时间分数阶Klein-Gordon型方程的各种精确解.
全文HTML
-
对于下列具有一般形式的时间分数阶非线性偏微分方程:
其中Dtα为卡普托型微分算子或者Riemann-Liouville型微分算子,
$u=u(x, t), n \in \mathbb{N}_{+}, t>0, x \in \mathbb{R}$ .方程(1)包含了许许多多非线性时间分数阶数学物理模型.求解形如方程(1)的分数阶非线性偏微分方程比求解整数阶非线性偏微分方程更加困难,因为大多数整数阶偏微分领域的求解方法不适用于分数阶偏微分方程领域,为此需要重新设计一个新的算法.值得一提的是,在文献[10-11]中,芮伟国教授率先提出了分离变量法与齐次平衡原理相结合的新方法.下面介绍这种方法的具体操作步骤:第1步:对形如类型(1)的时间分数阶非线性偏微分方程,将它们的解假设成下列两种形式:
或者
其中:v=v(x)为空间变量x的待定函数,a0,a1,λ,γ0,γ1为待定参数且均为常数,这些待定的函数和参数将在下一个步骤中加以确定;Eα,1(λtα)称为单参数Mittag-leffier函数,其分数阶导数定义为DtαEα,1(λtα)=λEα,1(λtα).由于(2)式带有一个常数a0,因此(2)式非常适合Caputo型微分算子下的运算,因为只有在Caputo型分数阶导数下,常数的导数才为零.显然,(3)式非常适合Riemann-Liouville型微分算子下的运算.下面仅以(2)式为例来说明第二个步骤的操作要领.
第2步:将(2)式代入到(1)式中必定可以得到下列形式的方程
像文献[10-11]中那样,利用齐次平衡原理,令Mittag-leffier函数Eα(λtα)的同次项的系数以及常数项分别等于零,会得到下列形式的一些常微分方程组
对常微分方程组进行求解,可以获得这些方程的解v=v(x)的具体表达式以及相关参数a0,a1,λ的取值.当这些函数和参数的值被确定之后,通过(2)式,不难获得形如方程(1)的时间分数阶非线性偏微分方程的各种精确解,具体操作见第3步.
第3步:将第2步中所获得的各种解v=v(x)的具体表达式以及相应的参数a0,a1,λ的值代入(2)式,就可获得方程(1)的各种精确解.使用类似的操作步骤和方法,利用(3)式,可以获得方程(1)的其他类型的精确解.
-
求解下列时间分数阶Klein-Gordon型方程[14]:
的精确解,其中u=u(x,t),t>0,x∈R,将方程(5)改写成
如果方程(5),(6)是Riemann-Liouville型分数阶导数定义下的分数阶偏微分方程,那么我们就假设方程(6)的解具有如下的形式
其中:c0,c1,γ0,γ1为待定参数,均为常数且c1≠0,γ0>-1,γ1>-1;函数v=v(x)为空间变量的待定函数.把(7)式代入方程(6)中可得
在(8)式中,令时间变量t的幂指数全部相等,可得
求解(9)式即得:
为简便起见,记
将(10)式代入(8)式中消去时间项t-4α后即得:
假设方程(11)具有下列m次多项式形式的解
根据齐次平衡原理可以确定最高次m的值.如果平衡方程(11)中线性项v与非线性项
$v \frac{\mathrm{d}^{4} v}{\mathrm{d} x^{4}}$ 中x的次数,即得m=4.类似地,如果我们平衡高阶线性项$\frac{\mathrm{d}^{2} v}{\mathrm{d} x^{2}}$ 和最高阶非线性项$v \frac{\mathrm{d}^{4} v}{\mathrm{d} x^{4}}$ 中x的次数,可得到m=2.将m=4代入(12)式可得
其中r0,r1,r2,r3,r4为待定系数.将(13)式代入(11)式即得
很容易发现方程(14)有两个孤立项-56ac12r42x6和-84ac12r3r4x5.显然,当且仅当r4=0时,两个项的系数都等于零.因此,方程(11)没有形如(13)式的解.
但如果将m=2代入(12)式中,却可得到
又将(15)式代入(11)式中,不难得到
在方程(16)中,让x的同次幂的所有系数都等于零,不难得到下列方程组:
解方程组(17),有
将(18)式代入(15)式可以得到待定函数v(x)的具体表达式
将(19)式和(10)式代入到(7)式中,就获得了方程(6)的一个精确解:
其中:c0,m 是任意常数,
$\mathit{\Omega } {\rm{ = }}\frac{{\mathit{\Gamma } \left( {1 - 2a} \right)}}{{\mathit{\Gamma } \left( {1 - 4a} \right)}},\;0 < a < \frac{1}{2}$ 且$\alpha \neq \frac{1}{4}$ .当方程(6)是卡普托型分数阶导数定义下的分数阶偏微分方程时,不妨假设方程(6)存在其它形式的解,即
其中:b0,b1,λ是待定参数,均为常数且b0≠0;v(x)是关于空间变量x的待定函数.将(21)式代入(6)式即得
在方程(22)中,令Eα(λtα)和Eα2(λtα)的系数都等于零可得下列方程组
首先求解(23)式中第一个线性常微分方程,只讨论Δ=a2b02-2bb0λ2>0的情况,可以得到2种形式的通解:
其中:
${\mathit{\Omega } _0} = \sqrt {\frac{{a{b_0} + \sqrt {{a^2}b_0^2 - 2b{b_0}{\lambda ^2}} }}{{2b{b_0}}}} $ ,${\mathit{\Omega } _1} = \sqrt {\frac{{a{b_0} - \sqrt {{a^2}b_0^2 - 2b{b_0}{\lambda ^2}} }}{{2b{b_0}}}} $ ,${\mathit{\Omega } _2} = \sqrt { - \frac{{a{b_0} + \sqrt {{a^2}b_0^2 - 2b{b_0}{\lambda ^2}} }}{{2b{b_0}}}} $ ;B1,B2,B3,B4,C1,C2,C3,C4为任意常数.为了计算简便,令B3=B4=0,将(24)式代入(23)式的第二个非线性常微分方程中得
令(26)式中
$\mathrm{e}^{2 \mathit{\Omega }_{0} x}$ 和$e^{-2 \mathit{\Omega }_{0} x}$ 的系数全部等于零,只需要$a^{2} b_{0}+a \sqrt{\Delta}-\frac{4}{3} b \lambda^{2}=0$ ,解得将(27)式及B3=B4=0代入到(24)式中得
将(28)式代入(21)式中可以得到方程(6)的2个精确解为
其中:b0,k1,k2为任意常数且b0>0.同样令B1=B2=0,类似可得到和(29),(30)相同形式的精确解,只需要将(29)和(30)式中的k1,k2改为k3,k4即可.
运用同样的方法,取C1=C2=0,在此条件下就可以得到方程(6)的另外2个精确解
其中b0,k5,k6为任意常数.
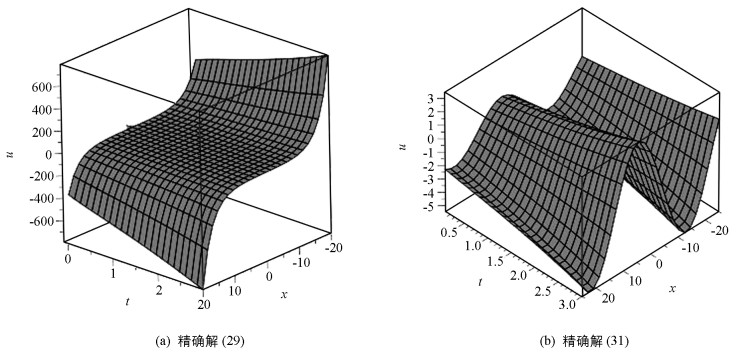
解(29)和(31)的3维坐标图形见图 1.



 下载:
下载: