为了顺利给出方程(1)的振动条件，首先给出引理1.

引理1^[17]  设A，B，C，F是定义在$\mathbb{R}$ⁿ上的n元可微函数，Γ是Ax+By+Cz=F确定的n参数平面族，Σ是Γ的包络，则Ax+By+Cz=F没有实根当且仅当没有Σ的切平面通过点(x，y，z).相应地，如果设$\widetilde A, \widetilde B, \widetilde F$是定义在$\mathbb{R}$ⁿ上的n元可微函数，$\widetilde {\mathit{\Gamma}} $是$\widetilde Ax + \widetilde By = \widetilde F$确定的n参数直线族，$\widetilde{\Sigma}$是$\widetilde {\mathit{\Gamma}} $的包络，则$\widetilde Ax + \widetilde By = \widetilde F$没有实根当且仅当没有$\widetilde{\Sigma}$的切线通过点(x，y).

定理1  方程(1)是振动的当且仅当p＜0，q＜0，$r < - \frac{2}{3}\left[{{{\left({ - \frac{1}{{3p}}} \right)}^{\frac{1}{2}}} + {{\left({ - \frac{1}{{3q}}} \right)}^{\frac{1}{2}}}} \right]$.

证  由于方程(1)是否振动主要由其特征方程是否有正根来判定，因此首先计算方程(1)的特征方程

进而在$\mathbb{R}$³内寻找特征方程(2)没有正根的区域.对于任意给定的正实数对(λ，μ)∈$\mathbb{R}$²，方程(2)都可以在$\mathbb{R}$³中确定一个平面，因此可将f(x，y，z，λ，μ)=0视为$\mathbb{R}$³上的关于λ，μ的双参数平面族.

根据包络的定义，由特征方程(2)所确定的双参数平面族的包络S上点满足

故

则

因此，当x＜0，y＜0时，有

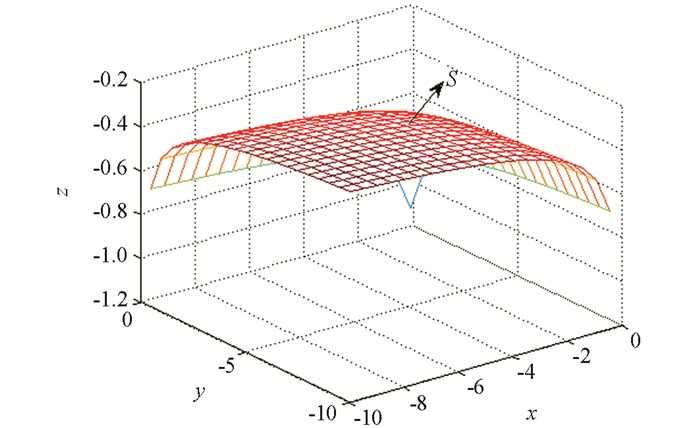
由文献[18]知，当x＜0，y＜0时，z(x，y)在(-∞，+∞)×(-∞，+∞)上是上凸函数且z(x，y)＜0(图 1).

由上凸函数z(x，y)的性质可知，当点(x，y，z)在包络S的下方区域时，不存在包络S的切平面通过点(x，y，z)，即当p＜0，q＜0，$r < - \frac{2}{3}\left[{{{\left({ - \frac{1}{3}p} \right)}^{\frac{1}{2}}} + {{\left({ - \frac{1}{3}q} \right)}^{\frac{1}{2}}}} \right]$时，方程(1)是振动的，同时由引理1可知，该条件为充要条件，故方程(1)是振动的当且仅当p＜0，q＜0，$r < - \frac{2}{3}\left[{{{\left({ - \frac{1}{{3p}}} \right)}^{\frac{1}{2}}} + {{\left({ - \frac{1}{{3q}}} \right)}^{\frac{1}{2}}}} \right]$.

证毕.

下面给出退化型偏差分方程(1)的振动条件.令特征方程(2)中的一个参数为零，则有

特征方程(5)对应的差分方程变为常差分方程

定理2  方程(6a)是振动的当且仅当p＜0，$r < - \frac{2}{3}{\left({ - \frac{1}{{3p}}} \right)^{\frac{1}{2}}}$或者p=0，r≥0；方程(6b)是振动的当且仅当q＜0，$r < - \frac{2}{3}{\left({ - \frac{1}{{3q}}} \right)^{\frac{1}{2}}}$>或者q=0，r≥0.

证  方程(6a)的特征方程为

(Ⅰ)当p=0时，特征方程(7)没有正根当且仅当r≥0；

(Ⅱ)当p≠0时，特征方程(7)的系数(p，r)可以看成是$\mathbb{R}$²内的点，只需在$\mathbb{R}$²内寻找使得特征方程(7)没有正根的点所在的区域即可.对于任意的正实数λ∈$\mathbb{R}$，方程(7)都可以在$\mathbb{R}$²中确定一条直线，因此可将f(x，y，λ)=0视为$\mathbb{R}$²上的单参数直线族，故由特征方程(7)所确定的单参数直线族的包络C上点满足

则

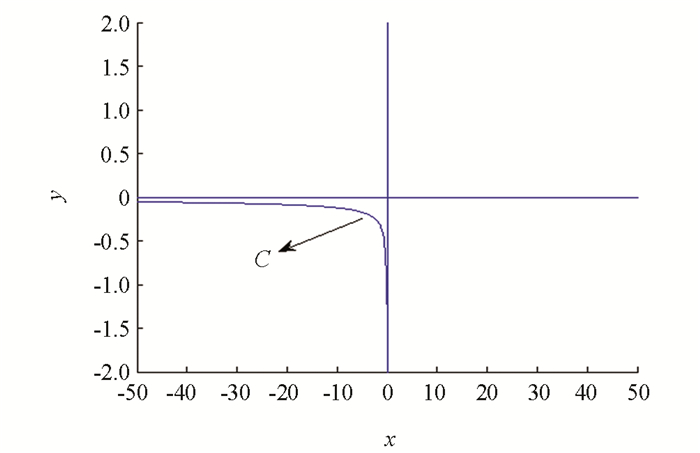
图 2为特征方程(7)所确定的直线族的包络C，且为第三象限中的上凸曲线，当点(p，r)在包络C的下方，即当p＜0，$r < - \frac{2}{3}{\left({ - \frac{1}{{3p}}} \right)^{\frac{1}{2}}}$时，方程(6a)是振动的，同时由引理1可知，该条件为充要条件，方程(6a)是振动的当且仅当p＜0，$r < - \frac{2}{3}{\left({ - \frac{1}{{3p}}} \right)^{\frac{1}{2}}}$或者p=0，r≥0.同理可证方程(6b)是振动的当且仅当q＜0，$r < - \frac{2}{3}{\left({ - \frac{1}{{3q}}} \right)^{\frac{1}{2}}}$或者q=0，r≥0.

证毕.

例1  给定偏差分方程

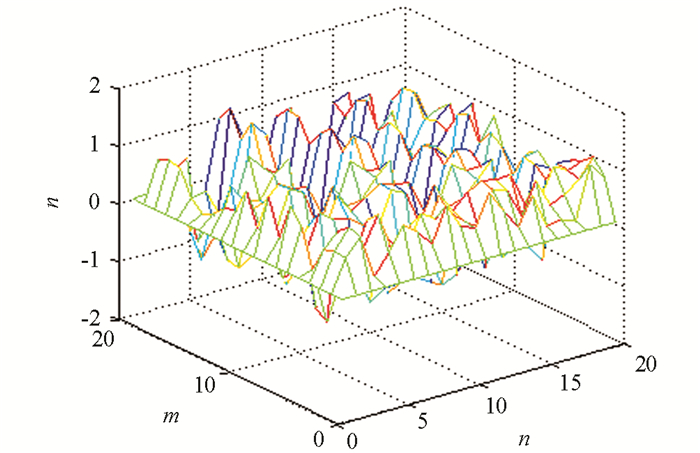
由定理1知，当p=-0.03＜0，q=-0.27＜0，$r = - 30 < - \frac{2}{3}\left[{{{\left({\frac{1}{{3 \cdot 0.03}}} \right)}^{\frac{1}{2}}} + {{\left({\frac{1}{{3 \cdot 0.27}}} \right)}^{\frac{1}{2}}}} \right] = - \frac{{80}}{{27}}$时，定理1条件满足，因此方程(1)振动(图 3).

例2  给定常差分方程

由定理2可知，当p=-2.43＜0，$r = - 0.9 < - \frac{2}{3}{\left({\frac{1}{{3 \cdot 2.43}}} \right)^{\frac{1}{2}}} = - \frac{{20}}{{81}}$时，定理2条件满足，因此方程(11)振动(图 4).