-
在这个大数据日益迅速发展的时代, 人们对于数据的价值已经越来越重视.根据IDC(International Data Corporation)的研究报告预测, 全世界数据总量将在2020年由2013年的4.4 ZB增长到35 ZB[1].数据挖掘作为一个重要的技术手段已经被广泛应用于各个领域的研究当中, 例如机器学习、模式识别、信息检索等[2-4], 而关联规则挖掘是数据挖掘中十分重要的手段之一, 特别是在大数据时代下进行数据间的关联分析显得尤为重要.由于大数据具有多样性的特点, 使用单个支持阈值来评估数据库中所有项目的发生频率是不够的, 因为每个项目不同, 它们不应该被同等看待.特别是在零售业, 价格低廉的日常用品经常被购买, 而奢侈品和高价位的产品却很少被购买; 如果设置过高最小支持度阈值, 只会挖掘到经常被购买的产品, 而较低的最小支持度阈值又会产生较多无意义的规则, 不利于产品的定位分析.所以, 传统的关联规则挖掘算法在处理海量数据时, 容易挖掘出常规的或无效用规则.
为了处理数据间的差异性问题, Liu等[5]首次提出一种多最小支持度框架下的关联规则算法MSApriori, 该算法通过给事务数据库中的每一个项目设定单独的最小支持度, 将经典的Apriori算法扩展到关联规则的挖掘中, 避免了设置单一支持度所产生的局限性.但是, 由于Apriori算法结构的缺陷, 需要多次扫描数据库容易受到组合爆炸的影响, Hu等[6]提出一种基于多最小支持度模式树的关联规则算法CFP-growth, 该算法基于FP-tree结构构造多最小模式树MIS-tree进行频繁项集的挖掘, 由于FP-tree模型的优点, 在挖掘过程中仅需2次扫描数据库来创建一系列条件模式树并生成完整的频繁项集, 在一定程度上节省了挖掘时间. Tseng等[7]提出了MMS_Cumulate和MMS_Stratify两种算法, 在分类的情况下允许多种形式的最小支持度定义, 并挖掘发现了广义的关联规则. Lee等[8]提出了一种基于最大约束条件下的多最小支持度关联规则算法, 在约束条件下进行关联规则挖掘, 并证明利用最大约束得到的关联规则数目小于使用最小约束得到的数目, 能够较为有效地减少无用规则产生.
随着研究深入, 更多的基于多最小支持度挖掘关联规则算法被提出, 例如基于属性关系多最小支持度的REMMAR算法[9]; 模糊定量序列模式关联规则算法FQDN-MMS[10]; 一种基于多最小置信度的关联规则算法[11]等.这些算法都从不同角度进行关联规则提取, 但是随着数据不断增大, 在挖掘过程中冗余造成时间和空间上的消耗, 并且会出现较多的冗余规则, 造成挖掘效率不高的问题.所以, 本文基于多最小支持度的定义, 通过改进CFP-growth算法在频繁项集的挖掘过程中进行优化:将频繁项目最小支持度值作为初始项目的支持度阈值进行数据预处理, 并在生成候选项集过程中利用排序向下闭合的属性进行冗余项删除, 以达到解决挖掘时间和减少冗余规则产生的目的.
全文HTML
-
设项目集合为I={i1, i2, …, in}, 事务数据库为D={d1, d2, …, dm}, 其中每一条事务为di(1≤i≤m), 由一个事务编号Tid表示, di为项目集合I的子集, 即
${d_i} \subseteq I$ (其中包含k个项的项集为k-项集); 若项集$X \subseteq I$ , 其在事务数据库中出现的频率, 即支持度计数记作Support(X).定义1 最小项支持度
对于上述项目集合I={i1, i2, …, in}, 对任意i∈I, 设定该项i一个最小支持度阈值, 称之为最小项支持度(minimum item support), 记作MIS(i). 表 1为某个数据库中各个项目所对应的MIS值.
定义2 最小项集支持度
对于项集X={is, …, it}, 1≤s≤t≤n, 其最小支持度为项集中最小的最小项支持度, 记作MIN(X), 即MIN(X)=min[MIS(is), …, MIS(it)].
定义3 频繁项集
在多最小支持度下, 若项i的支持度计数Support(i)>MIS(i), 则项i是频繁项; 若项集X的支持度计数Support(X)>MIN(X), 则项集X是频繁项集.
通过以上定义, 在频繁项集的挖掘过程中, 赋予事务数据库中每一项单独的最小支持度阈值, 能够更加确切地反应事务本身的特点, 因为得到的任意候选项集都是由其本身所需满足的最小支持度决定, 而不是统一的最小支持度, 所以基于多最小支持度关联规则算法的核心步骤为设定单独的支持度阈值, 通过统计得到项集的支持度计数, 再得到频繁项集, 并进一步得到关联规则.
-
由于CFP-growth算法中, 用于构造MIS-tree的标准仍然考虑了一些在高阶候选相机中不能产生任何频繁模式的项目, 同时在进行频繁项集的挖掘时, CFP-growth会递归地构建MIS-tree中各个项目条件模式树, 直到其各自的条件模式为空, 但是会构建一些不频繁项的条件模式基, 而这些条件模式基所构建的条件模式树则不会产生任何高阶频繁模式.因此, 本文基于上述问题会导致效率不高的现象进行如下改进策略.
-
根据上述定义可知, 在多最小支持度模型中, 判断项集是否为频繁项集是根据该项集中值最小的最小项支持度, 这与单支持度模型下进行频繁项集的判定不一样, 所以在多最小支持度下项集的最小支持度是一个变动的值, 并且取决于该项集中的项, 但是在多最小支持度模式下会出现频繁项集的子集可能不是频繁项集的情况.例如某项集X={b, e, h}为频繁项集, 根据表 1可知MIN(X)=MIS(e)=2, 但其子集Y={b, h}的MIN(Y)=MIS(h)=4则由于最小支持度阈值的改变, 其子集可能不是频繁项集.因此, 为了更好地进行频繁项集挖掘, 本文将项集中最小频繁项所对应的最小项支持度作为该项集的最小支持度阈值.
定义4 在多最小支持度下, 称LMS为所有频繁项集合中最小的MIS值.
例如项集X={a, b, c, d}, 若a, c, d为频繁项, 则
性质1 在事务数据库中, 若存在项集X={is, …it}且
$X \subseteq I$ , 那么当s≤k≤t时, 若Support(X)<LMS, 则Support(X)<min[MIS(is), …MIS(it)], 即项集X是非频繁项集.证 由于项集X的支持度小于LMS, 并且LMS又是频繁项目集合中最小的项, 所以根据定义3可以得到该项集X是非频繁项集.
性质2 在事务数据库中, 若存在2个项集X和Y,
$X \subset Y$ 且Support(X)<LMS, 则Support(Y)<LMS, 即项集Y是非频繁项集.证 由于在事务数据库中,
$X \subset Y$ , 则根据先验原理知Support(Y)≤Support(X), 又因为Support(X)<LMS, 则Support(Y)≤Support(X)<LMS, 根据性质1可知项集Y是非频繁项集.以上2个性质表明, LMS能够保证在多最小支持模式下获得的频繁项集具有全局反单调性, 并且在频繁项集的生成过程中使用LMS作为约束条件, 可用于修剪无法生成任何高阶频繁项集的项, 能够减少搜索空间和提高挖掘效率.
-
由于多最小支持度模式树的构建过程遵循了FP-tree思想, 并且该结构是将事务数据库中的每条事物按照项目的MIS值大小重新排序后进行构建, 所以在结构树中越靠下位置的项MIS值越小.因此, 考虑存在于树中的某一项i作为后缀项并构造其前缀子路径(即条件模式基)时, 该项i的MIS是其所有条件模式基中包含的项中最小的MIS值, 因此从该i的条件模式基中生成的任何频繁项集都大于i的MIS值.因此, 本文在挖掘频繁项集的过程中以该后缀项i的MIS作为该条件模树种的条件最小支持度,
定义5 当多最小支持度模式树存在一个项x, Support(x)是该项集X的支持度, 则MIS(x)表示为x必须满足的最小支持度阈值; Y是以x为后缀的条件模式基, y表示为该条件模式基Y中的一个项, 项y在该模式基中的支持度为Support(y), 其最小支持度为MIS(y), 则模式〈x, y〉的最小支持度为MIS(x).
-
由上所述可知, 在多最小支持度模式下, 若项集X是频繁项集, 那么它的子集可能是非频繁项集, 这与传统FP-growth算法中频繁项集向下闭合的性质有所差别, 这是由于其子集的最小支持度阈值发生了改变所导致的.在频繁项集的挖掘过程中, 为了将频繁项集向下闭合的性质能够重新适用于多最小支持度模式, 本文提出一种排序向下闭合的概念, 重新对该性质进行形式化定义, 为了更好地区别传统的挖掘方法, 一个按照序号排序好的k-项集表示为X={i1, i2, …, ik}.
性质3 (排序向下闭合)若存在一个频繁k-项集X={i1, i2, …, ik}(其中k≥2,
$X \subset I$ ), 且MIS(i1)≤MIS(i2)≤…≤MIS(ik), 那么任何包含项i1的k-1项集是频繁项集.证 由于项集X是频繁项集, MIS(i1)≤MIS(i2)≤…≤MIS(ik), 则根据定义2可知Support(X)>MIN(X)=MIS(i1), 假设项集
$Y \subset X$ 且i1∈Y, 则MIN(Y)=MIS(i1), 又因为项集Y是项集X的子集, 则Support(Y)≥Support(X), 所以Support(Y)≥Support(X)≥MIS(i1)=MIN(Y), 因此项集Y是频繁项集.根据性质3, 可以推导其反单调性.
性质4 若k-1项集X={i1, i2, …, ik-1}(
$X \subset I$ )是非频繁项集且MIS(i1)≤MIS(i2)≤…≤MIS(ik-1), 若存在一个ik∈I, 使MIS(i1)≤MIS(ik), 则k-项集也是非频繁项集.根据这2个性质就可以解决在多最小支持度模式下频繁项集的子集是否为频繁项的问题, 同时由于本文采用基于FP-tree结构的模式, 其构建条件模式树是按照各项的最小支持度进行路径排序的, 所以若后缀项不频繁, 那么它的所有超后缀项集也将不频繁.
1.1. 多最小支持度定义
1.2. 改进策略
1.2.1. 最小频繁项支持度(LMS)
1.2.2. 条件最小支持度
1.2.3. 排序向下闭合
-
基于设定单最小支持度容易造成效率不高的问题, 本文利用多最小支持度思想, 在挖掘过程中通过改进多最小支持度模式树和提高挖掘频繁项集效率进行关联规则提取.首先为项目集合I={i1, i2, …, in}中每一项设置独立的支持度MIS, 将事务数据库D={d1, d2, …, dm}中的每一条事务按照MIS大小顺序重新进行降序排列, 扫描排序后事务数据库, 按照FP-tree建立多最小支持度模式树NMIS-tree, 并构建项目头表Head-table, 根据定义4中LMS, 利用其性质将LMS值作为频繁项的筛选标准, 删除部分不能产生任何频繁项集的项, 并对初始NMIS-tree进行剪枝和合并, 得到完整的NMIS-tree.
在得到完整NMIS-tree后进行频繁项集挖掘, 利用Apriori中候选项集生成的方法得到每一项的候选项集, 并根据重新定义后排序向下闭合的性质, 对无法产生任何高阶频繁的项集停止挖掘, 减少冗余候选项集的产生.
-
多最小支持度模式树主要包含2个部分: MIS-List和前缀树节点. Head-table主要包含4个部分:项目名称(item), 支持度计数值(Sup), 各项最小支持度(MIS), 节点链接(node-link); 其中node-link表示为一个指针, 指向多最小支持度模式树中具有相同项目名的项. Head-table中所有项目的顺序按照MIS值大小进行降序排列.前缀树节点主要包含3个部分:项目名称(item), 支持度计数值(Sup), 节点链头(link).该步骤如下:
1) 将排序后的每一条事务按照MIS值顺序插入到NMIS-tree中, 得到初始NMIS-tree;
2) 删除初始NMIS-tree中的冗余项;
3) 合并NMIS-tree中可能包含相同路径的子节点, 得到完整的NMIS-tree.
具体描述过程如表 2所示.
其中, 过程insert_tree([p|P], T)表示将每一条事务中的项插入多最小支持度树中, 具体描述如表 3所示.
过程NMIS_Pruning(NMIS-tree, f)表示进行多最小支持度树中冗余节点删除过程, 具体描述如表 4所示.
过程MIN_Merge(NMIS-tree)表示进行多最小支持度树中相同节点的合并过程, 具体描述如表 5所示.
-
根据上述过程构建多最小支持度模式树NMIS-tree, 在得到频繁2-项集后, 通过Apriori中获取候选项集的方法得到高阶条件候选项集, 然后利用排序向下闭合的性质进行候选项集压缩, 最后进行频繁项集挖掘.具体描述过程如表 6所示.
-
数据预处理是将原始事务数据库进行重新排序.
表 7是一个包含10个事务的数据库, 从编号1到编号10分别对应不同的事务数据集.首先根据表 1所示的各项MIS值由大到小进行重新排序, 若存在相同MIS值得项则按照字母顺序进行排列, 最终得到排序后的事务数据库, 如表 8所示.
-
构建NMIS-tree是将排序后的事务数据库按照类似FP-tree的构建方法进行构建, 具体过程如下:
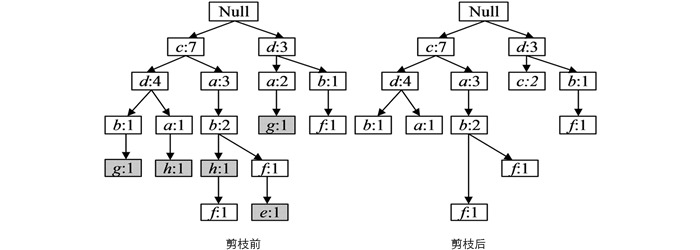
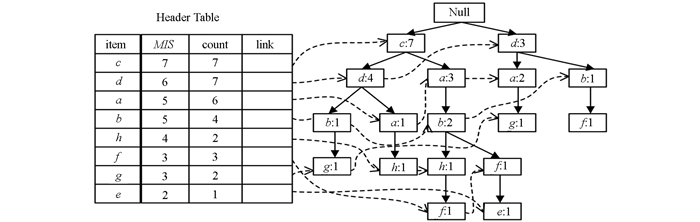
创建项目头表Header-Table, 其中包含项目名、各项的MIS值以及该项的支持度计数count, 其中item一栏按照MIS值从大到小的顺序进行排列; 创建根节点Null, 并将排序后事务数据库中的每一条事务插入到NMIS-tree中, 并更新记录各项的支持度计数, 最终得到初始NMIS-tree如图 1所示.
-
冗余剪枝是将项目头表中某些项进行删除, 通过前述中LMS的定义, 将LMS作为冗余项删除的标准, 并且删除与之对应的初始NMIS-tree中的节点, 具体过程如下:
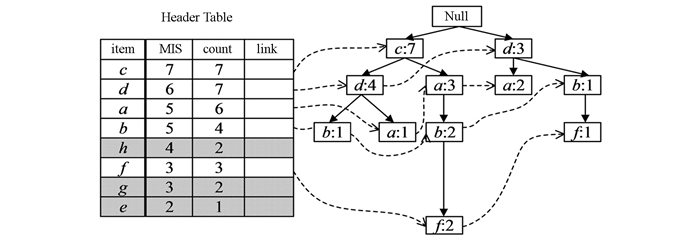
判断项目集合中的频繁项, 根据各个项目的Support和MIS, 按照定义3可知Header-Table中频繁项为{c}, {d}, {d}, {f}, 所以LMS=min[MIS(c), MIS(d), MIS(a), MIS(f)]=3, 则删除项为{h}, {g}, {e}, 并将对应NMIS-tree中的节点进行删除, 剪枝过程如图 2所示.
-
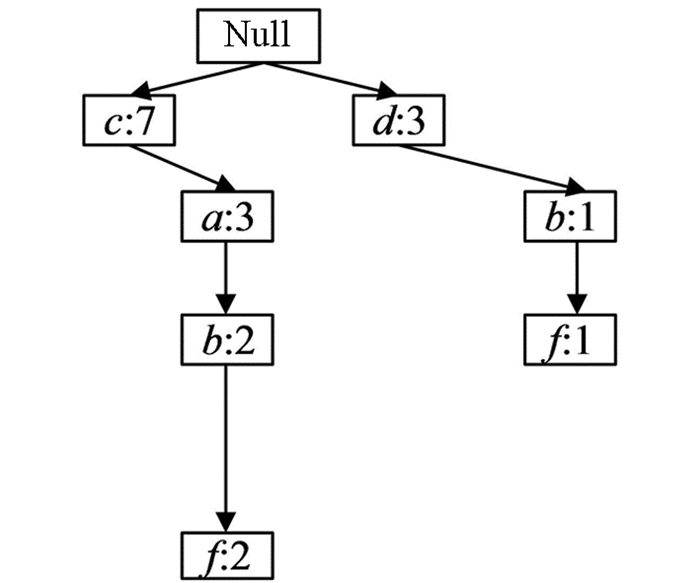
合并重复路径是将剪枝后NMIS-tree中链接在同一父节点的同名子节点进行路径合并, 支持度计数为该同名节点支持度计数之和.
遍历剪枝后的NMIS-tree, 节点〈b: 2〉含有同名但不同路径的子节点〈f: 1〉, 合并这2个子节点, 并重新计算支持度计数得到完整NMIS-tree, 如图 3所示.
-
在得到完整NMIS-tree之后, 按照项目头表中各项的MIS值从小到大进行频繁项集挖掘, 但是根据排序向下闭合的特性可知, 由于项a是非频繁项目, 以其为后缀建立的条件候选项集都是非频繁项集, 所以挖掘顺序从f→b→a→d→c变为f→b→d→c.
频繁项集挖掘过程从Header-Table最底端的项进行挖掘, 对于频繁项{f}, 以f为后缀项建立其前缀路径的条件模式如图 4所示.由于项f为频繁项, 从2-条件候选项集({b, f}, {a, f}, {c, f}, {d, f})进行挖掘.本文利用LMS性质进行频繁项集筛选, 由于只有项集{b, f}的支持度计数不小于LMS值, 所以得到{b, f}是频繁项集.
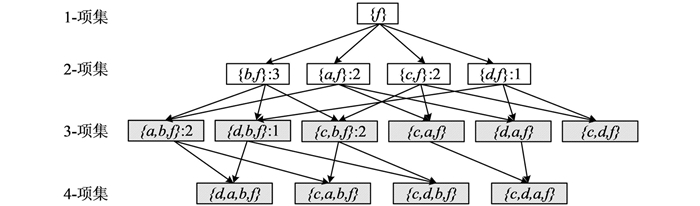
对于3-条件候选项集进行挖掘时, 本文通过使用Apriori算法中生成候选项集的方法得到3-条件候选项集, 为了更好地表明该步骤中利用了排序向下闭合中的反单调性, 将所有候选项集标出如图 5所示.例如通过项集{d, f}产生的3-候选项集{d, b, f}, {d, a, f}, {c, d, f}, 可以看到这些候选项集的最小支持度并没有发生改变, 并且最小支持度为MIS(f).所以, 根据性质3可以得到这些候选项集都是非频繁项集.因此, 当挖掘到2-项集时, 只需要将满足LMS值的项进行高阶项集挖掘, 其余项集已经自动停止挖掘, 所以能够减少大量候选项集的生成, 极大地提高了挖掘效率.而对于满足LMS的项集{b, f}, 由于其无法产生3-项集, 所以挖掘过程结束, 得到以f为后缀的频繁项集为{b, f}.
2.1. 算法思想
2.2. 算法流程
2.2.1. NMIS-tree构建
2.2.2. NCFP-growth
2.3. 算法示例
2.3.1. 数据库预处理
2.3.2. 构建NMIS-tree
2.3.3. 冗余剪枝
2.3.4. 合并重复路径
2.3.5. 频繁项集挖掘
-
本实验环境: CPU主频2.40 GHz, 内存8.00 GB, 操作系统为Windows 10, JAVA语言环境.本文采用表 9所示Transaction数据集和模拟合成的大规模数据集进行测试, 其中Transaction数据集包含40 000+记录、20种属性; 模拟合成数据集基于文献[12]中的方法, 生成不同数量的大规模数据集T10I4D100K.
对于每项MIS值设置如下:
其中, f(i)是项目i的实际频率, MS代表所有项目中最小的MIS值, σ用来控制项目的MIS值和发生频率之间的关系; 当σ=0时, 等同于在单一最小支持度下挖掘频繁项集.
-
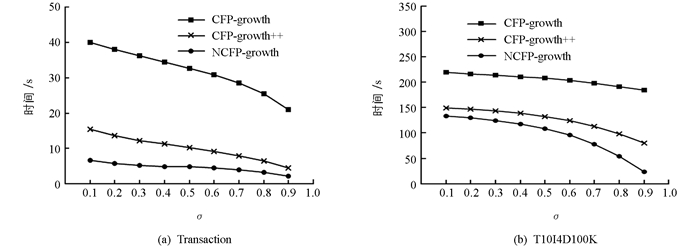
1) 图 6为Transaction和T10I4D100K两个数据集下不同σ值进行数据挖掘所耗费的时间分析, 本实验设置MS=0.001.
通过图 6可知, 在不同数据集中随着值的改变, 改进算法相比于CFP-growth和CFP-growth++算法表现得更加良好.随着σ值增大, 3种算法的挖掘时间都随之缩短, 改进算法在大数据集下的趋势表现更为明显, 这是由于σ值增大, 项目实际的支持度阈值也会被设置为一个较大的值, 较多的项目会被过滤, 所以构建的条件模式树较为稀疏, 挖掘频繁项集的数量会减少, 从而时间缩短幅度较大.
在Transaction数据集下, 随着σ值增加改进算法比CFP算法节省将近一个数量级的挖掘时间, 并且性能更加优越于CFP++算法, 这是由于改进算法在频繁项集挖掘过程中不需要每一项都向下进行挖掘, 因此提高了挖掘效率.在T10I4D100K数据集下, 由于设置的MS值非常小, CFP-growth必须构造大量的条件模式树进行频繁项集挖掘, 从而耗时过多.改进算法在构建条件模式树的过程中, 能够进行冗余节点删除和重复路径合并使结构树更加简洁, 避免了计算资源的浪费, 从而大幅度提高挖掘过程中的性能表现.
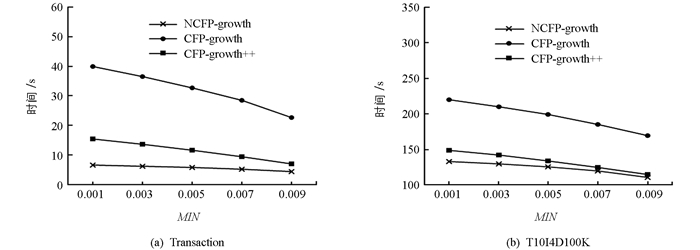
2) 图 7为Transaction和T10I4D100K两个数据集在不同MIN值下的挖掘时间对比(σ=0.2和σ=0.1).
以上2组实验分组在固定的σ值下, 为了更好地观察MIN值改变对于各个项目最小支持度的影响, 实验分别设定σ=0.2和σ=0.1, 将结果进行记录得到时间对比图如图 7所示.
通过图 7可知, 在不同数据集下通过固定σ值, 本文所提算法挖掘时间都少于CFP-growth和CFP-growth++, 并且明显优异于CFP-growth算法, 这说明了改进算法在挖掘频繁项集的过程中能够减少大量无用项集的产生, 提高挖掘效率; 同时随着MIN值增大, 改进算法和其余2种算法的挖掘时间都有所下降, 改进算法改变幅度较小, 而CFP-growth和CFP-growth++算法改变幅度较大, 这是由于较大MIN值会影响各个项目的最小支持度阈值, 从而改变多最小支持度模式树的结构, 使得候选项集的生成数目有所减少, 从而缩短挖掘频繁项集的时间.
-
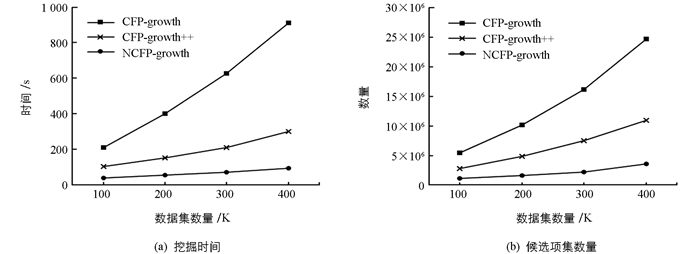
为了更好地分析算法的挖掘效率, 观察其可延展性, 通过设置不同数据量的同一数据集(T10I4D100K, T10I4D200K, T10I4D300K, T10I4D400K)进行对比分析如图 8.本实验设置MS=0.001, σ=0.5.
通过图 8可知, 3种算法随着数据集数量增加, 其挖掘时间和候选项集数量都呈一个近似线性增长, 但改进算法比CFP-growth和CFP-growth++算法表现出更高的效率.随着数据集数量增加, CFP-growth和CFP-growth++算法耗费时间明显增多, 改进算法呈现出较小幅度的变化, 并且在同一数据集下, 改进算法比CFP-growth节省将近一个数量级的时间, 表现出较高的挖掘效率, 这是由于数据集的数量增加, 前2种算法需要更多次数的递归调用进行挖掘, 而改进算法在挖掘频繁项集的过程中能够优化条件模式和减少递归次数, 从而较大幅度地降低挖掘时间.
通过图 8(b)中候选项集挖掘数量的对比可知, 随着数据集数量增加, 改进算法挖掘得到的候选项集数量增幅很小, 而CFP-growth和CFP-growth++算法增长幅度明显, 这说明了改进算法在大数据集下具有较高的稳定性和适应性.同时, 在同一数据集下, 改进算法得到的候选项集数量少于CFP-growth算法一个数量级之多, 低于CFP-growth++算法所耗费时间的一半, 这是由于改进算法在构造条件模式树挖掘频繁项集的过程中能够删除多余候选项集, 这也说明了改进算法在大数据集下能够较大程度地节省时间和提高效率.
3.1. 实验环境及数据
3.2. 实验结果分析
3.2.1. 时间消耗
3.2.2. 效率性能
-
本文在挖掘关联规则的过程中, 针对单一支持度算法的局限性以及挖掘效率不足的问题, 提出一种基于多最小支持度的挖掘算法.在挖掘关联规则的主要步骤即挖掘频繁模式的过程中, 以LMS值作为筛选标准, 在生成频繁项集的步骤中将无法产生频繁项集的候选项集直接删除, 从而快速得到频繁项集; 通过实验结果对比, 证明了本文所提改进算法能够大幅地提高挖掘效率, 并且在大规模数据集下的性能表现良好.由于数据规模的不断增大, 对于算法运行存储空间的要求越来越高.随着分布式储存和计算的迅猛发展, 如何利用有限的资源去获取数据价值的探讨和研究十分必要.



 下载:
下载: