-
百日咳是一种由伯德氏杆菌引起的传染性很强的急性呼吸道传染病,多数发生在幼年阶段的孩子中,但是现在青少年和成年人中的发病率也有所增加[1-2]. 2011年中国学者报道了一项包含多个地区临床中心的研究[3].目前为止,已有许多数学模型用来研究百日咳病菌传播机制,但在这些模型中,往往是将人群混合在一起讨论或只考虑幼年阶段人群才会感染.本文建立的模型,考虑了两阶段人群可以以不同的感染率相互感染.由于成年阶段人群对百日咳疾病具有较强的免疫力,百日咳疾病正在向无症状疾病演变[4-5],因此,成年阶段人群对幼年阶段人群的感染会在无意识下进行传播.在现实中,大多数不同阶段人群相互接触的最佳时机是在家庭之中,因此,家庭因素对百日咳疾病的传播起到了至关重要的作用[2].通过固定每个家庭成员的数量研究家庭流行病模型,可以得知家庭中每个感染者的具体变化并给出有效的接种策略控制百日咳疾病的传播[6-7],但对模型的理论研究有非常大的局限性.本文为避免这种局限性,通过固定两阶段人群同时在家庭中的时间来建立数学模型并分析其对百日咳疾病传播的影响.
由于刚出生的婴儿从母体得到的特异性抗体极少,我们假设刚出生的婴儿都是易感者.将人群分成幼年和成年两个阶段,假设在家庭内两阶段人群可以互相感染,且成年阶段人群对幼年阶段人群的感染率会相对较高;在家庭之外,由于幼年阶段人群多与同龄人群接触,且成年阶段人群之间的感染相对较弱,因此我们用一个相对比率σ来刻画这种关系.在这里不考虑疫苗作用可能无效的情况,即只要接种疫苗就完全有效.由于百日咳疾病多数发生在0~5岁的儿童,且青少年感染后症状不明显,因此假设幼年阶段的百日咳患者不会转化为百日咳成年患者.由于恢复期的变化对其他变量不会产生影响,因此,将其省略后得到模型:
其中:S1(t),S2(t),V(t),I1(t),I2(t)分别表示t时刻幼年阶段易感者、成年阶段易感者、接种者、幼年阶段感染者和成年阶段感染者的数量;μ表示自然死亡率,b表示成熟率,Λ表示幼年阶段人群的常数补充量,φ表示免疫缺失率,φ0表示疫苗接种率,β表示感染率,p表示在家庭之外的时间比率,kβ表示成年感染者对幼年易感者的感染强度,γ1和γ2分别表示幼年阶段感染人群和成年阶段感染人群的恢复率.我们在可行域
中讨论系统(1)解的性态.易证Ω是系统(1)的正向不变集.
全文HTML
-
易知系统(1)总是存在无病平衡点E0=(S10,S20,V0,0,0),其中
利用下一代矩阵的方法[8],很容易从系统(1)得到
根据下一代矩阵FV-1与基本再生数的关系,有
下面通过构造Lyapunov函数及应用Lyapunov-LaSalle's不变原理来证明无病平衡点的全局稳定性.
定理1 当
$\mathscr{R}_{v}$ <1时,无病平衡点E0是全局渐近稳定的.证 考虑Lyapunov函数
沿着系统(1)的任意解计算L1的导数得
在这里
E为2×2单位矩阵,并利用
有
由于代数平均值大于等于几何平均值,故
并且等式成立当且仅当S1=S10,S2=S20,V=V0.由于
$\mathscr{R}_{v}$ <1,从而L'1≤0.因此,由Lyapunov-LaSalle's不变原理[9],当$\mathscr{R}_{v}$ <1时,E0是全局渐近稳定的. -
如果系统(1)存在地方病平衡点(S1*,S2*,V*,I1*,I2*)∈
${{\mathbb{R}}^{5}}$ ,那么必然满足下面的方程组:从而有下面的等式成立:
由(4)式的第1式和第3式可以得到
其中:
由(4)式的第1式和第2式可以得到
联立(5)式可得
其中:
当
$\mathscr{R}_{v}$ >1时,因为(4)式的第1式和可行域的控制蕴含着D1<0,所以(6)式关于I1*有唯一正实根.根据(3)式和(5)式的表达式我们知道,并得到I2*>0,所以系统(1)有正平衡点E*=(S1*,S2*,V*,I1*,I2*)存在且唯一.因此,有下面的结论.命题1 如果
$\mathscr{R}_{v}$ >1,系统(1)存在唯一地方病平衡点E*.下面考虑E*的局部渐近稳定性和全局渐近稳定性.令
定理2 若
$\mathscr{R}_{v}$ >1,2hβ(S1*+σS2*)<γ成立,那么系统(1)的地方病平衡点E*局部渐近稳定.证 考虑系统(1)在E*处的Jacobian矩阵:
其中ψ=βI1*+(1-p)kβI2*.根据Gersgorin定理[10],如果下面的条件成立:
那么J (E*)的所有特征根都在区域
当中.经计算,矩阵J (E*)在条件2hβ(S1*+σS2*)<γ成立时,必有(7)式成立,因此J (E*)的所有特征值都在左半平面,即证明了E*是局部渐近稳定的.
接下来证明地方病平衡点的全局稳定性,在此之前,先给出两个记号
通过观察,明显得知W1与W2异号且由均值不等式可得W1+W2≥0.
定理3 若在E*是局部渐近稳定的条件下,还有W1与θ=(1-p)kI2*S1*-σI1*S2*异号,那么E*是全局渐近稳定的.
证 考虑Lyapunov函数
显然,对所有的(S1,S2,V,I1,I2)∈Ω有L2≥0,并且等式成立的充要条件是S1=S1*,S2=S2*,V=V*,I1=I1*,I2=I2*.沿着系统(1)的轨迹计算L2的导数得
又由于W1与θ异号,从而,当W1<0时,
当W1>0时,
另外由代数几何均值不等式和E*渐近稳定的条件可知L'2≤0,等式成立的充要条件是S1=S1*,S2=S2*,V=V*,I1=I1*,I2=I2*.因此,根据Lyapunov-LaSalle's不变原理可知,E*在Ω中是全局渐近稳定的.
1.1. 无病平衡点的存在性与全局稳定性
1.2. 地方病平衡点的存在性与稳定性
-
本节通过再生数的计算和数值模拟比较不考虑家庭因素条件和考虑家庭因素条件对百日咳疾病传播的影响.
根据基本再生数的表达式
可知
$\mathscr{R}_{v}$ 关于p值单调递减,其主要是描述成年阶段人群在家庭中对幼儿阶段人群的影响,也就是说,家庭所在时间比率只是对不同阶段人群之间的感染率会产生一定的影响,进而影响百日咳疾病的最终走向.特殊的,不考虑家庭因素对百日咳疾病传播的影响,此时就有相同的感染率,即只考虑幼年与幼年以及幼年对成年阶段的影响,即p=1.此时基本再生数满足且成年阶段感染者对幼年阶段易感者人群影响最小.从而可以从理论计算中得知,在一定条件下,家庭因素对百日咳疾病的传播具有推动作用.还可以考虑全是家庭因素的影响,即p=0,此时是一种极端的情况,且在现实中没有太大意义,故不作分析.当然,也可以讨论接种对百日咳疾病传播的影响,不过这已经被许多作者研究过,并得到疫苗接种对百日咳的控制具有重要的作用,这里不再赘述.接下来通过数值模拟说明家庭因素对百日咳疾病传播具体的影响是如何变化的.
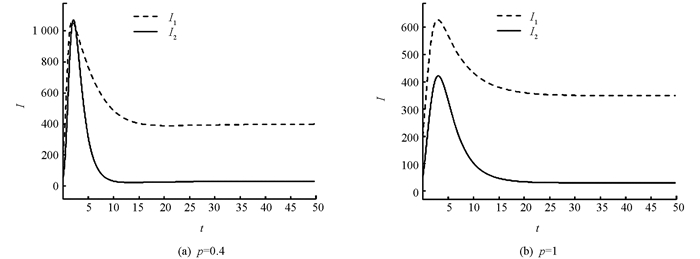
首先,假设系统(1)的部分参数为Λ=300,φ=0.05,φ0=0.3,b=μ=0.1,γ1=0.3,γ2=0.6,β=0.001,k=3,σ=0.3. 图 1表示对同一初值(S1,S2,V,I1,I2)=(1 500,3 000,1 010,200,50),不同p值下基本再生数
$\mathscr{R}_{v}$ >1时幼年阶段感染者I1和成年阶段感染者I2随时间变化的曲线图,这里不再讨论$\mathscr{R}_{v}$ <1的图像.比较这两幅图可以看到,I1,I2在图 1(a)中峰值处的数量接近于(b)中峰值处的两倍,当达到平衡状态时,在(a)中的数量也比(b)中的数量多.因此,随着p值的增加,I1的数量在不断减少,也就是说家庭因素对百日咳疾病的传播具有一定的推动作用.因此,有婴幼儿的家庭应当更加注重百日咳疾病的传播,除了对小孩子进行疫苗接种之外,还可以对家庭所有成员都进行一次百日咳疫苗的接种.
-
本文建立了具有接种和家庭因素且将人群分为幼年和成年两个阶段的百日咳模型,得到了基本再生数
$\mathscr{R}_{v}$ 的表达式,证明了$\mathscr{R}_{v}$ <1时无病平衡点是全局渐近稳定的,$\mathscr{R}_{v}$ >1时不稳定,当$\mathscr{R}_{v}$ >1时,存在唯一的地方病平衡点且在一定条件下证明了地方病平衡点的局部稳定性和全局稳定性.另外讨论了家庭因素对百日咳疾病传播的影响,随着p的增大,基本再生数$\mathscr{R}_{v}$ 减少,表明了家庭因素对百日咳疾病的传播具有一定的推动作用.



 下载:
下载: