高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

手的参与形式对触压觉类SNARC效应的影响

,  ,  , 

上一篇

下一篇

刘雍江, 臧运洪, 杨航, 等. 手的参与形式对触压觉类SNARC效应的影响[J]. 西南大学学报（自然科学版）, 2020, 42(10): 140-145. doi: 10.13718/j.cnki.xdzk.2020.10.018
引用本文: 刘雍江, 臧运洪, 杨航, 等. 手的参与形式对触压觉类SNARC效应的影响[J]. 西南大学学报（自然科学版）, 2020, 42(10): 140-145. doi: 10.13718/j.cnki.xdzk.2020.10.018
shu
Yong-jiang LIU, Yun-hong ZANG, Hang YANG, et al. TheImpactofthe Mannerof Hand Participationonthe SNARC-Like Effectof Touch-PressureSensation[J]. Journal of Southwest University Natural Science Edition, 2020, 42(10): 140-145. doi: 10.13718/j.cnki.xdzk.2020.10.018
Citation: Yong-jiang LIU, Yun-hong ZANG, Hang YANG, et al. TheImpactofthe Mannerof Hand Participationonthe SNARC-Like Effectof Touch-PressureSensation[J]. Journal of Southwest University Natural Science Edition, 2020, 42(10): 140-145. doi: 10.13718/j.cnki.xdzk.2020.10.018
shu

手的参与形式对触压觉类SNARC效应的影响

  • 兴义民族师范学院 教育科学学院，贵州 兴义 562400

  • 基金项目: 贵州省科学技术基金项目(黔科合LH字[2014]7405号)；贵州省教育厅青年科技人才成长项目(黔教合KY字[2017]374)
详细信息
    作者简介:

    刘雍江(1984-)，男，副教授，主要从事教学认知、文化认同的研究 .

  • 中图分类号: B842.1

TheImpactofthe Mannerof Hand Participationonthe SNARC-Like Effectof Touch-PressureSensation

  • School of Educational Science, Xingyi Normal University for Nationalities, Xingyi Guizhou 562400, China

  • 摘要: 为探究触压觉的类SNARC效应(空间—数字反应编码联合效应)以及手的参与形式在其中的作用，以131名大学生为被试，采用4个不同质量的圆柱体(比较刺激)和1个固定质量的圆柱体(标准刺激)作为实验材料，要求被试判断比较刺激与标准刺激的轻重，收集反应正确率.结果发现：当双手分别单独完成轻重比较任务时(实验1)，未表现出类SNARC效应；当双手共同完成轻重比较任务时(实验2)，表现出类SNARC效应，即左手对较轻刺激的反应正确率更高，右手对较重刺激的反应正确率更高.认为双手的参与形式影响触压觉类SNARC效应的表现.
    Abstract: In order to explore whether there exists SNARC (Spatial Numerical Association of Response Codes)-like effect in touch-pressure sensation and the role of hand involvement in it, a study was made, in which 131 college students were selected as subjects. Four cylinders different in weight (comparative stimulus) and one cylinder of fixed weight (standard stimulus) were used as experimental materials. The subjects were asked to judge the weights of comparative stimulus and standard stimulus, and the accuracy was recorded. The results showed that SNARC-like effect was not observed when the two hands completed the light-weight comparison task separately (Experiment 1); when the subjects completed the task of light-weight comparison with both hands (Experiment 2), they showed the SNARC-like effect, in other words, the left hand responded more accurately to the lighter stimulus, and the right hand responded more accurately to the heavier stimulus. In conclusion, the manner of hand participation affects the performance of SNARC-like effect in touch-pressure sensation.
  • 加载中

  • 图 1  右手与左手反应正确率之差与质量大小的回归模式图

    下载: 全尺寸图片 幻灯片

    表 1  单手完成任务时左右手对轻重圆柱体的反应正确率

    左手 右手
    轻 重 轻 重
    正确率/% 71.09±12.82 75.88±11.56 70.80±12.05 74.80±11.25
    下载: 导出CSV

    表 2  双手完成任务时左右手对轻重圆柱体的反应正确率

    左手 右手
    轻 重 轻 重
    正确率/% 74.07±15.55 68.47±16.37 66.98±15.03 73.41±14.16
    下载: 导出CSV
  • [1] DEHAENE S, BOSSINI S, GIRAUX P. The Mental Representation of Parity and Number Magnitude[J]. Journal of Experimental Psychology: General, 1993, 122(3): 371-396. doi: 10.1037/0096-3445.122.3.371
    [2] DEHAENE S, DUPOUX E, MEHLER J. Is Numerical Comparison Digital? Analogical and Symbolic Effects in Two-digit Number Comparison[J]. Journal of Experimental Psychology: Human Perception and Performance, 1990, 16(3): 626-641. doi: 10.1037/0096-1523.16.3.626
    [3] 刘超, 买晓琴, 傅小兰.不同注意条件下的空间-数字反应编码联合效应[J].心理学报, 2004, 36(6): 671-680. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xlxb200406006
    [4] 沈模卫, 田瑛, 丁海杰.一位阿拉伯数字的空间表征[J].心理科学, 2006, 29(2): 258-262. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xlkx200602001
    [5] 刘雍江, 林泳海.壮族大学生一位数字词的SNARC效应[J].心理科学, 2013, 36(4): 832-836. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xlkx201304012
    [6] NUERK H C, WOOD G, WILLMES K. The Universal SNARC Effect[J]. Experimental Psychology, 2005, 52(3): 187-194. doi: 10.1027/1618-3169.52.3.187
    [7] 张宇, 游旭群.负数的空间表征引起的空间注意转移[J].心理学报, 2012, 44(3): 285-294. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xlxb201203001
    [8] 孙悦亮, 郑伟意, 何先友.纯小数加工的心理机制:选择通达还是平行通达?[J].心理学报, 2017, 49(5): 611-621. doi: http://www.cnki.com.cn/Article/CJFDTOTAL-XLXB201705005.htm
    [9] DODD M D, VAN DER STIGCHEL S, ADIL LEGHARI M, et al. Attentional SNARC: There's something Special about Numbers (let us Count the Ways)[J]. Cognition, 2008, 108(3): 810-818. doi: 10.1016/j.cognition.2008.04.006
    [10] GEVERS W, REYNVOET B, FIAS W. The Mental Representation of Ordinal Sequences is Spatially Organized[J]. Cognition, 2003, 87(3): B87-B95. doi: 10.1016/S0010-0277(02)00234-2
    [11] doi: http://www.sciencedirect.com/science/article/pii/S0010945208709389 GEVERS W, REYNVOET B, FIAS W. The Mental Representation of Ordinal Sequences is Spatially Organised: Evidence from Days of the Week[J]. Cortex, 2004, 40(1): 171-172.
    [12] PREVITALI P, DE HEVIA M D, GIRELLI L. Placing Order in Space: the SNARC Effect in Serial Learning[J]. Experimental Brain Research, 2010, 201(3): 599-605. doi: 10.1007/s00221-009-2063-3
    [13] NUERK H, IVERSEN W, WILLMES K. Notational Modulation of the SNARC and the MARC (Linguistic Markedness of Response Codes) Effect[J]. The Quarterly Journal of Experimental Psychology Section A, 2004, 57(5): 835-863. doi: 10.1080/02724980343000512
    [14] 周玉.顺序及数量特性对SNARC效应的影响[D].苏州: 苏州大学, 2013.
    [15] 刘雍江, 左全顺, 郭增辉, 等.贵州少数民族儿童青少年SNARC效应的发展[J].心理科学, 2018, 41(5): 1138-1144. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=676454848
    [16] PROCTOR R W, CHO Y S. Polarity Correspondence: a General Principle for Performance of Speeded Binary Classification Tasks[J]. Psychological Bulletin, 2006, 132(3): 416-442. doi: 10.1037/0033-2909.132.3.416
    [17] 张丽, 陈雪梅, 王琦, 等.身体形式和社会环境对SNARC效应的影响:基于具身认知观的理解[J].心理学报, 2012, 44(10): 1309-1317. doi: http://www.cnki.com.cn/Article/CJFDTotal-XLXB201210006.htm
    [18] LOETSCHER T, SCHWARZ U, SCHUBIGER M, et al. Head Turns Bias the Brain's Internal Random Generator[J]. Current Biology, 2008, 18(2): R60-R62. doi: 10.1016/j.cub.2007.11.015
    [19] 葛慧.身体运动对SNARC效应的影响[D].武汉: 华中师范大学, 2014.
    [20] 胡林成, 熊哲宏.符号数量和非符号数量的空间表征: 5岁儿童的SNARC效应和距离效应[J].心理科学, 2016, 39(2): 364-370. doi: http://www.cnki.com.cn/Article/CJFDTotal-XLKX201602017.htm
    [21] RUSCONI E, KWAN B, GIORDANO B, et al. Spatial Representation of Pitch Height: The SMARC Effect[J]. Cognition, 2006, 99(2): 113-129. doi: 10.1016/j.cognition.2005.01.004
    [22] DENG Z J, CHEN Y H, ZHANG M, et al. The Association of Number and Space under Different Tasks: Insight from a Process Perspective[J]. Frontiers in Psychology, 2018, 9: 957. DOI: 10. 3389/fpsyg. 2018. 00957.
    [23] MOYER R S, LANDAUER T K. Time Required for Judgements of Numerical Inequality[J]. Nature, 1967, 215(5109): 1519-1520. doi: 10.1038/2151519a0
    [24] CAMPBELL J I D. The Handbook of Mathematical Cognition[M]. New York: Psychology Press, 2005.
    [25] doi: http://www.ncbi.nlm.nih.gov/pubmed/15478760 ITO Y, HATTA T. Spatial Structure of Quantitative Representation of Numbers: Evidence from the SNARC Effect[J]. Memory & Cognition, 2004, 32(4): 662-673.
    [26] doi: http://psycnet.apa.org/record/2005-11470-005 NUERK H, BAUER F, KRUMMENACHER J, et al. The Power of the Mental Number Line: How the Magnitude of Unattended Numbers Affects Performance in an Eriksen Task[J]. Psychological Science, 2005, 47(1): 34-50.
    [27] 高在峰, 水仁德, 陈晶, 等.负数的空间表征机制[J].心理学报, 2009, 41(2): 95-102. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xlxb200902001
    [28] WOOD G, NUERK H C, WILLMES K. Crossed Hands and the Snarc Effect: Afailure to Replicate Dehaene, Bossini and Giraux (1993)[J]. Cortex, 2006, 42(8): 1069-1079. doi: 10.1016/S0010-9452(08)70219-3
  • 加载中
图( 1) 表( 2)
计量
  • 文章访问数:  1525
  • HTML全文浏览数:  1525
  • PDF下载数:  104
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-03-10
  • 刊出日期:  2020-10-20

手的参与形式对触压觉类SNARC效应的影响

    作者简介: 刘雍江(1984-)，男，副教授，主要从事教学认知、文化认同的研究
  • 兴义民族师范学院 教育科学学院，贵州 兴义 562400
  • 收稿日期:  2019-03-10
基金项目:  贵州省科学技术基金项目(黔科合LH字[2014]7405号)；贵州省教育厅青年科技人才成长项目(黔教合KY字[2017]374)

摘要: 为探究触压觉的类SNARC效应(空间—数字反应编码联合效应)以及手的参与形式在其中的作用，以131名大学生为被试，采用4个不同质量的圆柱体(比较刺激)和1个固定质量的圆柱体(标准刺激)作为实验材料，要求被试判断比较刺激与标准刺激的轻重，收集反应正确率.结果发现：当双手分别单独完成轻重比较任务时(实验1)，未表现出类SNARC效应；当双手共同完成轻重比较任务时(实验2)，表现出类SNARC效应，即左手对较轻刺激的反应正确率更高，右手对较重刺激的反应正确率更高.认为双手的参与形式影响触压觉类SNARC效应的表现.

English Abstract

    全文HTML

  • 空间—数字反应编码联合效应SNARC(spatial-numerical association of response codes)效应首先被Dehaene等人[1]发现，该效应是指当人们对数字进行奇偶分类时，左手对小数字(如，1-4)的反应快于右手，右手对大数字(如，6-9)的反应快于左手.这是数字具有空间属性的一个直接证据.在此之前，Dehaene等人[2]在数字大小比较中就发现了类似效应.之后，研究者们在各种数值型[1, 3-8]及非数值型[9-12]材料的反应时任务中均发现了SNARC效应.值得注意的是，有研究者在正确率指标上发现了类SNARC效应.比如，在要求被试对不同形式数字进行奇偶判断的研究中发现，被试右手对大数字的反应正确率高于左手，左手对小数字的反应正确率高于右手[13]; 另以“百千万亿兆”为材料，要求被试进行大小比较的研究发现[14]，被试左手对小计数单位的反应正确率更高，右手对大计数单位字的反应正确率更高; 还有研究[15]发现3~5年级的少数民族儿童在对阿拉伯数字的奇偶判断中，表现出左手对小数字的反应更准确，右手对大数字的反应更准确的类SNARC效应.这些证据说明SNARC效应存在的广泛性.

    对如何理解SNARC效应，存在不同的假设.其中心理数字线的假设认为人们心理存在一条模拟的数字线，小数字表征在数字线左侧，大数字表征在数字线右侧[2].而Proctor等[16]提出的两极对应理论认为，可选择的刺激和反应均可编码为正极(+)和负极(-).对于SNARC效应，“大”编码为“+”极，“小”编码为“-”极; 在左、右的反应选择中，“+” “-”极分别与“右” “左”对应; 在上和下的反应选择中，“+” “-”极分别与“上” “下”对应，且刺激和反应极性吻合时的反应速度快于二者极性不吻合时的反应速度[16].该理论可解释水平和垂直的SNARC效应.

    过去的研究多从信息加工的角度理解SNARC效应[17]，近年来，随着具身认知的兴起，为我们理解数字认知提供了新的视角.比如，Loetscher等[18]考察被试在头的不同偏向下产生随机数字的情况，结果发现当被试把头偏向左边时，报告更多的小数字; 把头偏向右边时，报告更多的大数字; 葛慧[19]采用随机报告法范式进一步探究头和手在不同运动条件下SNARC效应的情况，结果发现，相对于静止状态，被试抬左手时报告更多的小数字，抬右手时报告更多的大数字; 头和手运动方向一致时，出现SNARC效应，头和手运动方向不一致时，没有出现SNARC效应.另有研究发现[17]，身体形式对SNARC效应存在影响，当被试双手同时分别对奇数、偶数或者偶数、奇数做反应时，表现出SNARC效应; 但是被试单独单手(左手或右手)对奇数或者偶数做反应时，没有表现出SNARC效应.这些研究结果表明，身体形式及其运动状态对数字及其空间表征的认识、理解有影响.

    已有的研究主要关注视觉[6, 15, 20]、听觉条件[5-6, 21]下的SNARC效应，并形成了较为一致的结果，即无论视觉材料(阿拉伯数字、数字词、点阵、面积)还是听觉材料(数字声音、音调)均存在SNARC效应.其他感觉通道(如，触压觉)呈现的刺激是否能表现出SNARC效应尚不明确.过去研究多关注反应时指标上的SNARC效应[5, 6, 17, 22]，以正确率为因变量指标的研究较少，对此，本研究采用轻重比较任务(借鉴之前研究中的大小比较任务)操纵手的参与形式，探索触压觉通道是否存在正确率上的SNARC效应，并结合具身认知和两极对应理论对研究结果做分析解释.此外，数字信息在心理数字线上的表征还表现出其他特殊效应，比如距离效应，它是指在大小判断任务中，被试比较2个在数量上相差大的数字比比较2个在数量上相差小的数字更容易，正确率更高[23].距离效应是反映数量大小信息得到激活的一个重要指标.为检验轻重判断任务是否与过去研究中的大小比较任务一样激活数量信息，本研究亦对距离效应进行了分析.

1.   实验1左右手分别对刺激进行轻重判断

    1.1.   被试

  • 被试为兴义民族师范学院64名在校大学生，其中男生31人，女生33人，平均年龄(21.55±1.21)岁.所有被试均为右利手，视力及矫正视力正常.

    • 1.2.   实验设计

  • 采用2(质量：88 g，92 g为轻; 108 g，112 g为重)×2(手：左手; 右手)被试内实验设计.因变量为正确率.

    • 1.3.   实验材料及仪器

  • 从质量鉴别仪中选择5个圆柱体，质量分别为88 g，92 g，100 g，108 g，112 g，其中以88 g，92 g，108 g，112 g的圆柱体作为比较刺激，在这些圆柱体后面用铅笔分别标上数字1，2，3，4; 100 g作为标准刺激.

    • 1.4.   实验程序

  • 根据各个圆柱体背面的标号，按照拉丁方设计事先安排好刺激呈现的顺序.被试端坐在实验台前，戴上眼罩，将一只手(左手或者右手)放在桌面上，以肘关节为支撑点，手掌心朝上距离台面约20 cm.主试坐在被试对面，将比较刺激和标准刺激先后放在被试的手掌中央位置，要求被试判断第二个刺激与第一个刺激孰轻孰重，主试做好记录.一只手做完实验后，换另一只手.按先左手、后右手做轻重判断，或者先右手、后左手做轻重判断的顺序进行实验，2种顺序安排进行被试间平衡.对每只手而言，标准刺激在比较刺激之前、之后的次数各占一半，标准刺激轻于、重于比较刺激的次数各占一半，且顺序上均进行被试内平衡.刺激在手掌停放时间为2 s，比较刺激和标准刺激间隔1 s.每做一次判断为一个试次，2个试次之间间隔约5 s.每个被试需要完成64个试次.被试每完成32个试次，休息2 min.总共需时约12 min.

    • 1.5.   结果与分析

  • 收集被试左手和右手判断比较刺激与标准刺激孰轻孰重的正确率，64名被试的平均数和标准差见表 1，其中“轻”代表 88 g和92 g，“重”代表108 g和112 g.

    参照Dehaene等人[1]的方法检验SNARC效应，对反应正确率进行2(质量：轻重对比)×2(手：左右手对比)重复测量方差分析，结果表明：手的主效应不显著[F(1，63)=0.24，p＞0.05];质量主效应显著[F (1，63)=8.77，p＜0.01，ηp2=0.12]，对较重物体的反应正确率显著高于对较轻物体的反应正确率; 手和质量大小的交互作用不显著[F(1，63)=0.094，p＞0.05].说明单手进行质量判断时，未能引发正确率上的SNARC效应.

    此外，基于距离效应是数字比较任务中代表数量信息得到激活的重要指标，本研究也对其进行检验，并主要从正确率上进行分析，若被试对距离较远的刺激的反应正确率高于对距离较近的刺激的反应正确率，说明出现了距离效应.本研究中，92 g、108 g与100 g均相差8 g，88 g、112 g与100 g均相差12 g，将前者定为近距离，后者定为远距离.使用配对样本t检验对远距离与近距离下的正确率进行比较，结果发现二者差异具有统计学意义[t(63)=5.552，p＜0.001]，远距离的反应正确率(76.90%)显著大于近距离的反应正确率(69.38%)，出现了距离效应，说明本研究中的轻重判断任务激活了数量信息.

    本研究在单手进行轻重判断任务中未发现类SNARC效应，这与张丽等人[17]的研究结果相似，但与Dehaene等人[1]认为SNARC效应与从左到右的表征有关，而与左右手无关的观点相悖.因此，为进一步澄清手对SNARC效应的影响，本研究接下来对2只手共同完成实验的表现进行研究.

2.   实验2双手共同对刺激进行轻重判断

    2.1.   被试

  • 67名在校大学生，均未参加实验1，其中男生35人，女生32人，平均年龄(20.76±1.36)岁，所有被试均为右利手，视力及矫正视力正常.

    • 2.2.   实验设计

  • 同实验1.

    • 2.3.   实验材料及仪器

  • 同实验1.

    • 2.4.   实验程序

  • 在一个试次中，被试2只手同时放在桌面上，标准刺激和比较刺激分别先后呈现在被试左手、右手或者右手、左手，要求被试判断后一刺激比前一刺激孰轻孰重.整个实验中，标准刺激在比较刺激之前、之后的次数，轻于、重于比较刺激的次数均相等，且先后顺序均进行被试内平衡.标准刺激出现在左手、右手的次数相等，对其出现在左手、右手上的先后顺序进行被试间平衡.其它程序与实验1相同.

    • 2.5.   结果与分析

  • 收集被试左右手判断比较刺激与标准刺激孰轻孰重的正确率，67名被试的平均正确率和标准差见表 2.

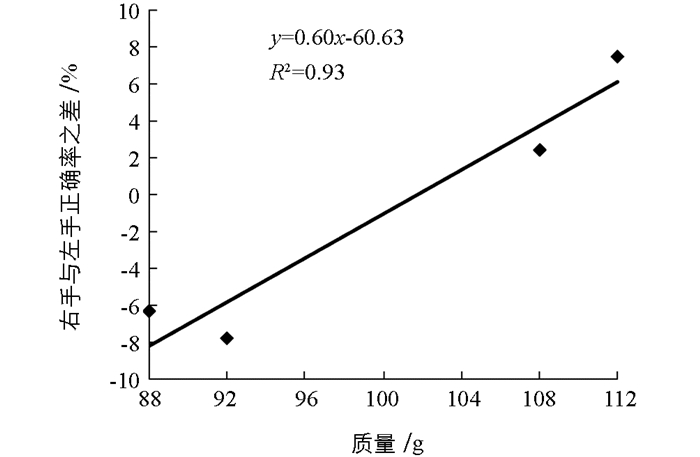
    2×2重复测量方差分析表明，手的主效应不显著[F(1，66)=0.84，p＞0.05];质量大小主效应不显著[F(1，66)=0.072，p＞0.05];手和质量大小的交互作用显著[F(1，66)=4.89，p＜0.05，ηp2=0.07]，说明出现了正确率上的SNARC效应.基于前人研究[1, 6, 24]，本研究进一步做回归分析，首先计算每个刺激上被试右手、左手反应正确率之差，然后建立刺激对平均正确率之差的回归方程，最后检验回归系数的正负以确定此效应的方向.分析结果表明，平均回归系数为0.60，与0的差异达到显著水平[t(66)=2.51，p＜0.05].回归模式图见图 1，由该图可知，对于质量小的圆柱体(88 g，92 g)，右手与左手的反应正确率之差为负数，说明左手对质量小的圆柱体的反应正确率更高; 对于质量大的圆柱体(108 g，112 g)，右手与左手的反应正确率之差为正数，说明右手对质量大的圆柱体的反应正确率更高，表明确实出现了类SANRC效应.

    此外，本研究使用配对样本t检验对远距离与近距离下的正确率进行了比较，结果发现，二者差异具有统计学意义[t (66)=4.171，p＜0.001]，远距离的反应正确率(73.51%)显著大于近距离的反应正确率(67.96%)，出现了距离效应.说明轻重判断任务激活了数量信息.

3.   讨论

  • 本研究借鉴已有研究中的大小比较任务，首次使用轻重比较任务考察被试对刺激的轻重判断是否表现出正确率上的SNARC效应.以往研究中的大小比较任务通常以阿拉伯数字(如，1-9，5除外)为比较刺激，要求被试判断比较刺激与目标刺激(如，5)的大小，比较左右手对小数字、大数字的反应快慢以检验SNARC效应[25-27].而本研究选取质量鉴别仪中的88 g，92 g，108 g，112 g的圆柱体作为比较刺激，100 g的圆柱体作为标准刺激，先后将比较刺激和标准刺激呈现给被试，让其报告二者孰轻孰重，通过比较左右手对较轻、较重刺激的反应正确率来检验类SNARC效应.

    本研究实验1结果发现，当把比较刺激和标准刺激放在一只手上进行轻重判断时，没有表现出触压觉上的类SNARC效应，与张丽等人[17]一项研究中的结果相似.说明身体参与形式对类SNARC效应存在影响.从具身认知的角度看，当每只手单独完成任务时，身体不能形成自左向右的表征，因而导致刺激的空间表征不能表现出来.

    实验2的结果发现，当把比较刺激和标准刺激分别放在2只手上进行轻重判断时，表现出触压觉上的类SNARC效应，即左手对质量较轻刺激的反应正确率高于右手，右手对质量较重刺激的反应正确率高于左手，说明双手参与是产生触压觉类SNARC效应的重要条件.原因可能是当双手参与共同完成任务时，身体能够形成自左向右的表征，激发了质量刺激的空间表征.本研究结果与张丽等人[17]、Wood等人[28]的观点一致.在Wood等人[28]的研究中，被试以交叉手的方式按键完成对多种材料(阿拉伯数字、数字词、听觉数字、骰子)的奇偶判断任务，结果均未表现出SNARC效应，他们据此认为身体的空间形式对SNARC效应存在一定影响.而本研究与张丽等人[17]的研究结果则直接表明了SNARC效应(本研究中为类SNARC效应)的具身性.

    此外，基于极性编码理论，被试的左右手分别对应“-”和“+”极，刺激的轻重分别对应“-”和“+”极.当手和刺激极性相匹配时，反应正确率高; 当手和刺激极性不匹配时，反应正确率低，从而产生类SNARC效应.虽然本研究实验1也涉及左右手及轻重刺激，但没出现类SNARC效应.本研究认为，实验1中被试左右手是单独完成任务的，左手完成一半任务，右手完成另一半任务，每个试次中正、负极性是分开出现的(每次轻重判断涉及一只手).而实验2中，左右手是共同完成任务的，正负极性都出现(每次轻重判断涉及2只手).因此，本研究推断在实验任务每个试次中(即一次轻重判断或奇偶判断)，仅具备刺激的正负极性，而没有反应主体正负极性的完整出现，难以引发类SNARC效应.

    上述推断可解释张丽等人[17]的研究结果，该研究实验2包括4个组块，每个组块均为单手对奇数或偶数做反应，虽然具备了数字的正负极性，但是手的正负极性未能出现在一个组块中，因此不能出现SNARC效应; 该研究实验3考察不同合作情境下SNARC效应的情况，结果发现身体位置和左右手完全一致时(即左侧位置的被试用左手、右侧位置的被试用右手共同完成任务)出现SNARC效应; 该实验涉及刺激、身体位置、手三者的极性，当身体位置的正负极性和手的正负极性一致时，才能使2个被试构成的反应主体表现一致的正负极性，即左为“-”极，右为“+”，其他条件下(被试位置和反应手完全不一致，部分一致)，身体位置的极性(如左侧为“-”极)和反应手的极性(右手为“+”极)可能会抵消，使得反应主体不能在该实验任务中表现完整的正负极性，这样即使刺激的正负极性完整，也不能出现SNARC效应.对于Wood等人[28]要求被试交叉手完成奇偶判断任务未发现SNARC效应的结果，亦可解释为左右手极性和双手交叉后右、左侧位置(以身体中线分)极性抵消，而使反应主体不能表现完整正负极性导致SNARC效应消失.当然，此推断有待进一步实证检验.

    此外，本研究实验1和实验2均出现了距离效应，表明被试对刺激的轻重判断均激活了刺激的数量信息.不过，只有实验2出现了类SNARC效应，这说明数量信息的激活能引发距离效应，但不一定能引起类SNARC效应.从认知的具身性来看，类SNARC效应易受身体形式的影响，而距离效应则相对稳定，不受身体形式的影响.

    总之，本研究通过质量轻重判断任务发现了触压觉的类SNARC效应，说明SNARC效应的广泛性.且身体形式对触压觉类SNARC效应存在影响，说明数字认知有一定的具身性.另外，本研究基于两极对应理论对类SNARC效应进行了解释和推断，强调在每个试次中，身体和手构成的反应主体的极性完整性对SNARC效应的影响.不过在使用该理论做解释时，身体位置、手的极性仍然涉及身体形式，表明身体形式对SNARC效应的影响.最后发现，距离效应稳定存在于2个实验中，这在一定程度上意味着并非所有的认知过程都有具身性.

参考文献 (28)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回