-
慢性丙型肝炎病毒(HCV)感染在全球影响约1.3亿至1.5亿人,是肝硬化和肝癌的主要原因[1]. 干扰素和利巴韦林的治疗只能使不到50%的患者消除病毒[2]. 为了提高HCV的治愈率,新治疗方案集中在直接抗病毒药物(DAAs)的开发上. 为了研究DAAs治疗的效果,科学家们开发并改进了区分和量化丙肝病毒RNA正链和负链的新方法. 一些考虑丙肝病毒RNA正链和负链的动力学模型被构建出来研究DAAs治疗下的丙肝病毒动力学性态. 特别地,文献[3-5]考虑了DAAs治疗对丙肝病毒RNA正链动力学性态的影响;文献[6]同时考虑了丙肝病毒RNA的正链和负链,但其没有区分RNA正链分别用于翻译和复制的情况;文献[7]中的模型同时考虑了丙肝病毒RNA的正链和负链,并区分了用于翻译和复制的RNA正链,但其常微分方程模型没有考虑DAAs治疗,同时对相关模型的理论分析还非常不完整. 基于上述分析,本文在文献[7]模型的基础上结合DAAs治疗得到如下动力学模型:
其中:Rt表示用于翻译的丙肝病毒RNA正链的数量;Rc,Rm分别表示复制复合物中用于复制的丙肝病毒RNA正链、负链的数量;μt是Rt的自然衰退率,Rc与Rm的自然衰退率均是μc;Rc可以从复制复合物和膜质网中穿出到细胞质中,以θ速率变为Rt;Rt从细胞质进入膜质网并与复制复合物的蛋白质相互作用,并以σ的速率变为Rc;Rc和Rt可以组装进入病毒粒子中,并以ρ的速率分泌出病毒粒子;在复制复合物中,Rm可以通过最大速率r复制Rc形成,Rc以速率α通过复制Rm形成;εs表示药物治疗对病毒分泌的影响,εα表示药物治疗对Rc的影响,εr表示药物治疗对Rm的影响,εi=1(i=s,α,r)对应于100%有效的药物,εi=0(i=s,α,r)对应于完全无效的药物,所以一般假设0<εi<1(i=s,α,r);kt表示药物治疗改变Rt降解速率的效果,kc表示药物治疗改变Rc与Rm降解速率的效果,一般假设ki≥1(i=t,c). 假定宿主因子限制RNA负链的复制,因此当达到最大数量Rmax时,复制按照logistic生长定律减慢.
全文HTML
-
依据模型生物意义,我们给定系统(1)非负初始条件:
定理1 对于给定的初始条件(2),系统(1)的所有解都是非负的,且在
$ \mathbb{R}_{+}^{3}$ 中最终有界.证 首先证明系统(1)解的非负性. 假设在某一时刻t1,某个变量率先取到0,其余变量为正,不妨设Rt(t1)=0,Rc(t1)>0,Rm(t1)>0. 则由系统(1)的第1个方程可得:
知Rt将恢复正性.
假设在某一时刻t2,某2个变量率先取到0,其余变量为正,不妨设Rt(t2)=Rm(t2)=0,Rc(t2)>0. 则由系统(1)的第2个方程可得:
假设在某一时刻t3>t2,有Rc首次取到0,即Rc(t3)=0. 则由系统(1)可得:
从而Rt,Rm将恢复正性.
假设在某一时刻t4,3个变量同时取到0,即Rt(t4)=Rm(t4)=Rc(t4)=0,此时有
显然Rt,Rm,Rc将一直为0. 重复上述证明过程,可得系统(1)解的非负性.
下面证明系统的耗散性. 由解的非负性及系统(1)第3个方程易知:
将系统(1)第1个方程和第2个方程相加可得:
进而由解的非负性可以得到:
其中d=min{ktμt,kcμc}. 再由比较原理可得:
从而系统的耗散性得证. 定理证毕.
由定理1的证明,可以得到系统(1)存在如下不变区域:
-
易见系统(1)总是存在边界平衡点E0(0,0,0). 计算可得基本再生数
$R_{0}=\frac{b \theta \sigma+s m w}{b m n} $ ,其中m=σ+(1-εs)ρ+ktμt,s=(1-εα)α,n=θ+(1-εs)ρ+kcμc,w=(1-εr)r,b=kcμc. 则由简单计算可知当R0>1时,系统(1)存在唯一的正平衡点E*(Rt*,Rc*,Rm*),其中对于相关平衡点的局部稳定性,我们有如下定理:
定理2 (i)当R0<1时,边界平衡点E0(0,0,0)局部渐近稳定;
(ii) 当R0>1时,正平衡点E*(Rt*,Rc*,Rm*)局部渐近稳定.
证 (i)系统(1)在E0处的特征方程为
其中
注意到θ<n,σ<m,可得mn-θσ>0. 同时当R0<1时,有bn-ws>0. 从而易知ai>0,i=1,2,3. 进一步计算可得:
再次由mn-θσ>0,bn-ws>0,可得a1a2-a3>0. 从而根据Routh-Hurwitz稳定性判据可知,当R0<1时,特征方程(4)的所有根均具有负实部,从而知边界平衡点E0(0,0,0)是局部渐近稳定的.
(ii) 系统(1)在E*处的特征方程为
其中
易知bi>0,i=1,2,3. 进一步计算可得:
由mn-θσ>0,可知b1b2-b3>0. 从而根据Routh-Hurwitz稳定性判据可知,当R0>1时,特征方程(5)的所有根均具有负实部,从而知正平衡点E*(Rt*,Rc*,Rm*)局部渐近稳定. 定理证毕.
-
定理3 (i)当R0<1时,边界平衡点E0(0,0,0)全局渐近稳定;
(ii) 当R0>1时,正平衡点E*(Rt*,Rc*,Rm*)全局渐近稳定.
证 (i)根据上述定理1和定理2,只需证明平衡点的全局吸引性. 构造如下Lyapunov函数:
对函数V1(t)沿系统(1)的解求导可得
当R0<1时,易见
$\frac{\mathrm{d} V_{1}(t)}{\mathrm{d} t} \leqslant 0 $ 且$\frac{\mathrm{d} V_{1}(t)}{\mathrm{d} t}=0 $ 仅当Rc=0时成立. 将Rc=0代入系统(1)第1个方程和第3个方程,可以得到Rt→0及Rm→0. 从而由Lyapunov-LaSalle不变原理可知,当R0<1时,无病平衡点E0(0,0,0)全局吸引,从而全局渐近稳定.(ii) 令g(x)=x-1-lnx(x>0). 构造如下Lyapunov函数:
对函数V2(t)沿系统(1)正解求导,并利用正平衡点E*满足的等式可得:
注意到当x>0时,g(x)≥g(1)=0. 由此可知当R0>1时
$\frac{\mathrm{d} V_{2}(t)}{\mathrm{d} t} \leqslant 0 $ ,且$\frac{\mathrm{d} V_{2}(t)}{\mathrm{d} t}=0 $ 仅当Rt=Rt*,Rm=Rm*及Rc=Rc*时成立. 从而根据Lyapunov-LaSalle不变原理,当R0>1时,正平衡点E*(Rt*,Rc*,Rm*)是全局渐近稳定的.理论研究表明,系统(1)的全局动力学性态完全由基本再生数R0决定,从而为了研究DAAs治疗对疾病控制的影响,只需知道DAAs治疗各参数对R0的影响. 特别地,由R0的如下表达式
可知当通过DAAs治疗使得治疗相关参数εs增大时,即减小分泌病毒的速率时,会使得R0增大,此时可能会增加细胞内病毒RNA的浓度;当使得相关参数εα,εr,kt,kc增大时,即减小Rc与Rm之间的复制速率以及增大Rt,Rc与Rm的降解速率时,会使得R0减小,从而有利于疾病控制.
-
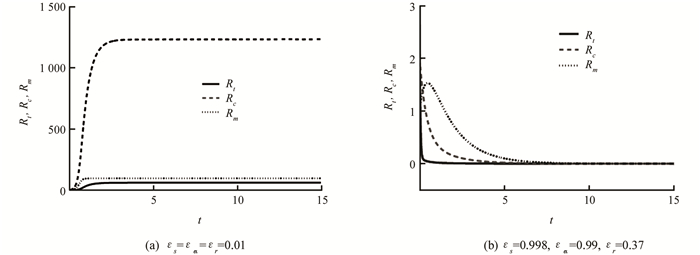
为了探究DAAs治疗对丙肝病毒RNA动力学性态的影响,取定一组参数ρ=0.1,θ=1.2,σ=0.1,μt=24,μc=1.05,α=30,r=3.18,Rmax=100,kt=kc=1,使εs,εα,εr作为控制参数而变化. 当εs=εα=εr=0.01时,可以计算出基本再生数R0=37.911 5,此时系统(1)存在平衡点Rt*=61.177 3,Rc*=1 233.690 2,Rm*=97.367 7且是全局渐近稳定的(图 1(a)),可见此时治疗效果不佳;当εs=0.998,εα=0.99,εr=0.37时,可以计算出基本再生数R0=0.256 6,知系统(1)的边界平衡点是全局渐近稳定的(图 1(b)),Rt,Rc,Rm最终趋于零,说明此时采取的治疗十分有效. 由此可见,系统(1)可以用来研究DAAs治疗抑制丙肝病毒复制的效果.



 下载:
下载: