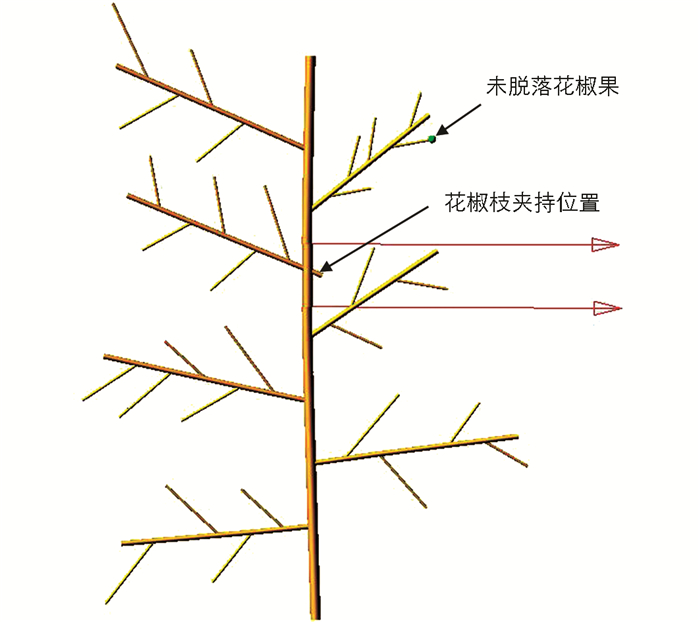
本研究的花椒果样品来自重庆市璧山区某种植大户花椒种植园，随机选取30株下桩后的花椒枝进行花椒枝形态数据测量，如图 1(a)所示. 从这些花椒枝中随机选取50粒花椒果进行力学特性测量，测量仪器为ELK-30型高精度数显推拉力计(伊莱科电气有限公司，精度0.01 N)，如图 1(b)所示，测量结果如表 1所示.

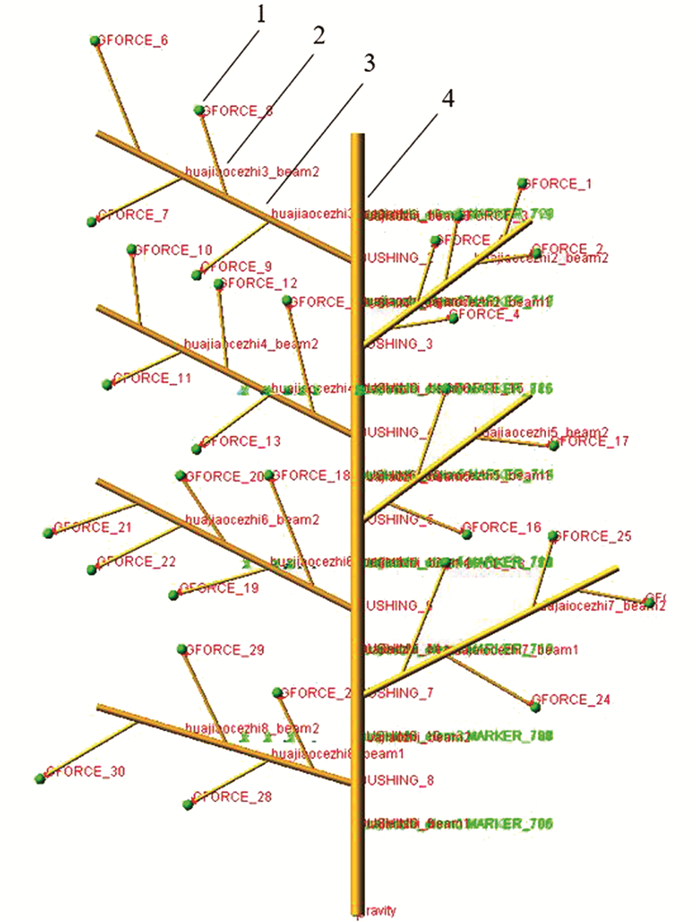
根据花椒枝形态数据，利用ADAMS中的离散柔性连杆建立花椒枝柔性体，柔性体长度450 mm，直径8 mm. 该柔性体是直接将多个单元刚体通过柔性梁连接，通过刚体间的柔性连接变形来模拟柔性体的变形，单元刚体不能变形，模型本质上仍属刚体范畴，这种柔性体构建方法简单、求解效率高，适合变形体一般问题求解和定性分析^[5-6].

花椒果脱落的形式主要有两种：一是由于果柄组织结构脆弱而导致花椒果和果柄一起脱落；二是由于花椒果与果柄之间细胞分化导致脱果^[7]. 从花椒果力学特性可知，果柄与树枝之间的结合力约为花椒果与果柄之间结合力的两倍，本研究只考虑花椒果与果柄之间的脱落. 在ADAMS中利用离散柔性连杆建立果柄模型，并在果柄与树枝之间施加固定约束.

花椒果脱落可以采用传感器和脚本仿真配合的方式控制，这种方法可以简单地控制花椒果按照预定的情况脱落，但难以在一个仿真过程中控制多个花椒果独立脱落，本研究采用广义力与传感器配合的方式来控制花椒果与果柄的连接和脱落^[8]，广义力由3个分量的力和3个分量的力矩组成^[9]. 为尽可能模拟实际情况，从测量的50粒花椒果中随机选取30粒，将其力学特性添加到模型中，并为每个花椒果添加其对应质量. 在花椒果和果柄之间施加一个广义力，广义力的施加需要两个作用点，均位于果柄与花椒果的连接处. 然后进行花椒果质心加速度测量，设置传感器以监测花椒果的加速度，当检测的加速度大于临界加速度时，花椒果和果柄之间的广义力大于结合力，当广义力变为0，花椒果脱落. 取花椒果和果柄之间结合力的刚度K为400 N/m，阻尼系数C采取默认值，更改广义力6个组成部分的函数，其中沿x方向的分力F_x为

式中，IF()为判断函数；SENVAL()用以返回传感器触发的时间；DX()为位移函数；VX()为速度函数；SENSOR_1是探测两个作用点之间距离的传感器；MARKER_185是位于花椒果上的作用点；MARKER_186是位于果柄上的作用点；K为广义力刚度系数；C为默认阻尼系数.

建立的花椒枝果柔性体模型如图 2所示.

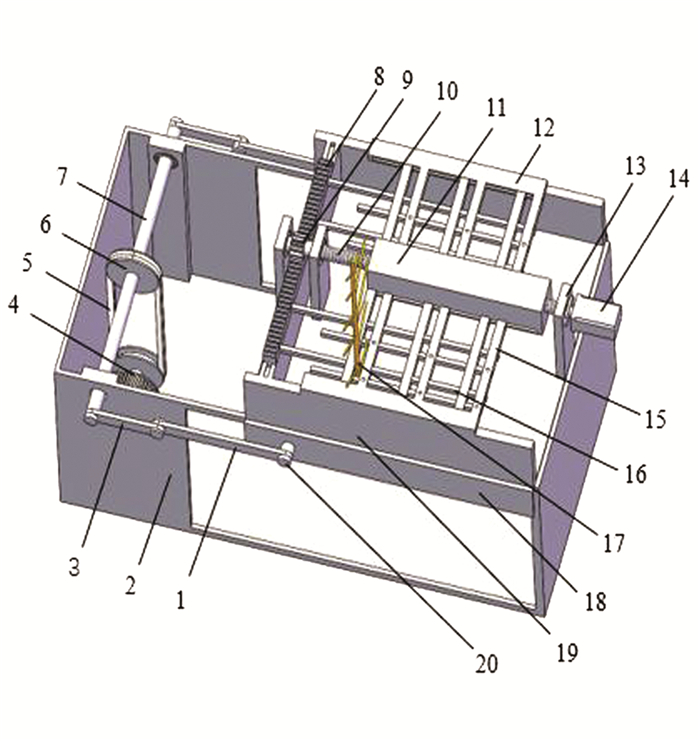
振动式花椒采摘机主要由机架、传动机构和振动机构组成，如图 3所示. 传动机构由传动电机、带轮、带、传动轴、曲柄、摇杆组成. 振动机构由振动台、水平移动块、支撑立柱、丝杆、齿条、齿轮、步进电机组成. 振动台通过底部的凹槽与机架配合，振动台的两侧挡板上设有固定柱，两侧支撑板上设有固定挡块. 振动台的中间位置水平方向上设有支撑立柱，支撑立柱之间设有水平移动块，水平移动块的两侧也设有固定挡块，水平移动块的内部配合有丝杆，丝杆的一端固定有齿轮，另一端与步进电机输出轴固定连接. 齿轮与齿条啮合，齿条的底部设有滑块，一侧设有夹持块.

将花椒枝放入由固定挡块和夹持块组成的通口内，启动步进电机，丝杆顺时针转动，使水平移动块向靠近步进电机方向移动. 同时，齿轮转动，带动齿条及夹持块向左侧滑动. 水平移动块和夹持块同时靠近固定挡块将花椒枝摆正夹紧. 夹紧后，步进电机停止，传动电机带动曲柄连杆机构摇杆摆动，从而实现振动台的水平往复运动. 振动台带动夹持的花椒枝受迫振动，花椒果受到振动惯性力作用，当振动惯性力大于花椒果与果柄间的结合力时，花椒果脱落.

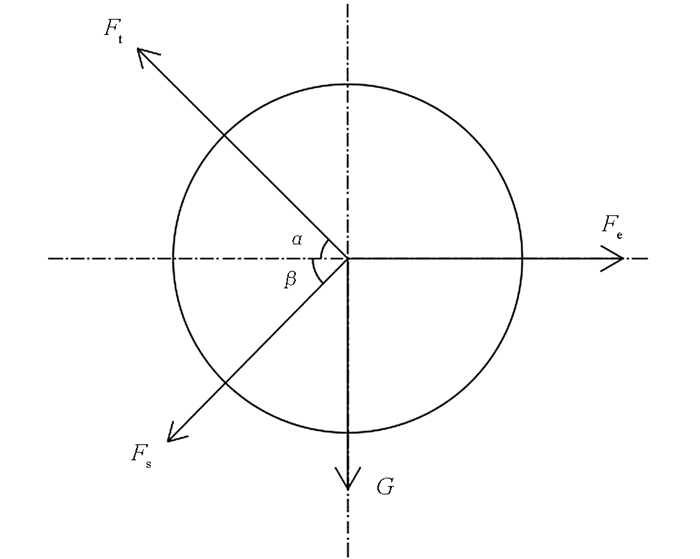
振动台的振动方式为水平方向上的往复运动，但因侧枝及果柄韧性相对较好，花椒果在竖直方向上也会发生一定的摆动，因而将花椒果的运动看做是花椒枝的往复运动和花椒果随着果柄定点摆动的复合振动形式^[10]. 在振动过程中，花椒果主要受到果柄的拉力F_t、剪切力F_s、重力G及惯性力F_e作用，其中，拉力和剪切力构成花椒果与果柄之间的结合力，花椒果的受力模型如图 4所示.

花椒振动采摘过程中，花椒果的运动方程为^[11]

式中，X是水平方向位移，m；t是时间，s；A是振幅，m；ω是角速度，rad/s；φ是初始相位角，rad；ε是阻尼比.

花椒果受到的惯性力可表示为

式中，F_e是惯性力，N；m是质量，kg.

花椒果受振动脱落的条件为

式中，F_t是拉力，N；F_s是剪切力，N；α是拉力与水平方向的夹角，rad；β是剪切力与水平方向的夹角，rad.

驱动振动台的曲柄连杆机构本质上是一曲柄滑块机构，如图 5所示. 曲柄长度L₁和转速ω决定了振动台的振幅和振动频率，选取合适的曲柄长度与转速是获得脱落效果的关键^[12].

建立如图所示坐标系，x为水平方向，y为竖直方向，坐标原点位于曲柄旋转中心A. 则振动台(即滑块)水平方向位移可表示为

式中，x是振动台的水平方向位移，m；L₁是曲柄长度，m；L₂是摇杆长度，m；α₁是曲柄与水平方向上的夹角，rad；β₁是摇杆与水平方向上的夹角，rad. α₁=ω₁t，ω₁为曲柄转速，rad/s；t为时间，s.

对于α₁和β₁，下式成立：

则有：

将式(7)泰勒展开并忽略高阶小量可得

将式(8)代入式(5)可得

因而，振动台水平方向的加速度可表示为

振动台水平方向的运动由两个谐振动组合而成，分别为L₁cos(ω₁t)和$ \frac{{L_1^2}}{{4{L_2}}}({\rm{cos}}\left( {2{\omega _1}t} \right) - 1)$，两个谐振动叠加后，其运动中心为$ {\rm{ - }}\frac{{L_1^2}}{{4{L_2}}}$，周期T为$ \frac{{2\pi }}{{{\omega _1}}}$，最大加速度a_max为$ {L_1}\omega _1^2\left( {1 + {\rm{ }}\frac{{{L_1}}}{{{L_2}}}} \right)$，因而，振动台水平方向位移本质上仍然是谐振动方程^[13].

考虑到振动式花椒采摘机结构较为复杂，且花椒枝在振动过程中为高频响应，容易引起积分求解器的求解失败. 为提高求解成功率，本研究将采摘机简化为曲柄滑块机构，在曲柄与地面之间、曲柄与摇杆之间、摇杆与滑块之间建立旋转约束，在滑块与地面之间建立水平位移约束，在滑块与花椒枝之间建立固定约束，如图 6所示.

选取曲柄长度、曲柄转速和夹持高度作为试验因子，因子水平如表 2所示. 曲柄转速因子1，2，3对应的振动台振动频率分别为36，38，40 Hz. 夹持高度为夹持位置距花椒枝底端的高度. 按正交表L₉(3⁴)安排试验方案，试验结果如表 3所示. 仿真参数设置为：仿真时间为5 s，步数为200步，积分格式为SI2，容错量为3，初始步长为1×10^-11.

振动式花椒采摘机传动机构是基于曲柄滑块机构理论进行设计的. 将采摘机的三维模型分模块导入ADAMS中，对相关的部件施加约束，具体约束情况如表 4所示.

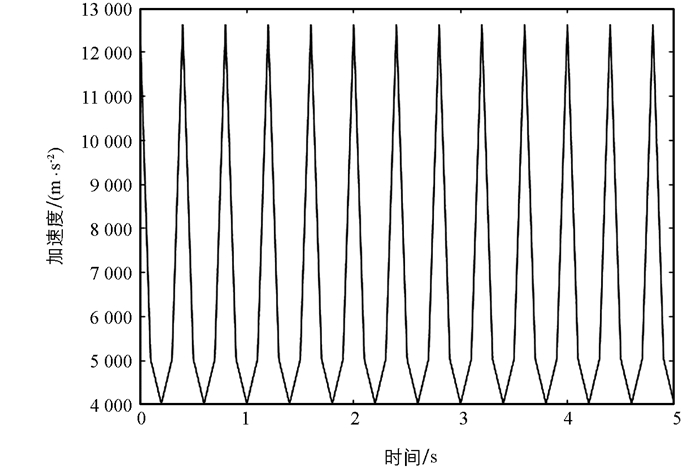
对于振动式花椒采摘机而言，花椒果脱落的条件是惯性力大于花椒果与果柄之间的结合力. 本研究通过对比振动台最大加速度的计算结果和运动学仿真结果来验证采摘机的传动机构能否达到预期工作效果. 取曲柄长度L₁为150 mm，曲柄转速为75π rad/s，摇杆长度L₂为300 mm，由式(10)计算出振动台的最大加速度a_max为12 479 m/s². 在ADAMS中，对模型施加驱动，驱动施加在转动轴与机架之间的转动副上，测量振动台质心加速度，设置仿真结束时间为5 s，步数为200步，仿真结果如图 7所示. 振动台的最大加速度仿真值为12 635 m/s²，与计算值误差为1.26%，满足设计要求.

在对花椒振动采摘过程中，振动台一直处于振动状态，对振动台进行模态分析，获得其振型及固有频率，以避免外部激励频率与其固有频率相等，进而避免共振发生.

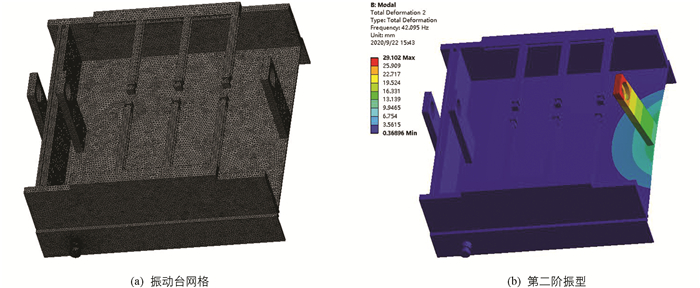
采用ANSYS Workbench对振动台进行模态分析. 默认结构材料为钢，密度7 085 kg/m³，弹性模量2×10¹¹ Pa，泊松比0.3. 对振动台进行网格划分，网格尺寸5 mm，将软件中Transition设置为Slow，以降低网格之间的增长比，使得网格过渡更平稳；将Span Angle Center设置为Fine，以提高振动台轴承座区域网格精度，其余保持默认设置. 振动台网格如图 8(a)所示，网格节点数为618 304，单元数为358 834，网格平均质量为0.802 32，质量较好，满足需求^[14].

振动台在工作过程中主要做水平方向的往复运动，模态分析时只保留水平方向位移的自由度，其余设置为0. 由于低阶振动比较危险，外界大多是低阶激励频率，且阶次越高，共振振幅越小，共振带来的危险性越低，因而本次模态分析只计算振动台前6阶振型^[15]，模态分析结果如表 5所示. 其中，第二阶振型如图 8(b)所示.

由表 5可知，振动台1阶固有频率接近于0 Hz，这是为了贴合实际运动情况，在给振动台施加边界条件时，没有限制其在水平方向上的位移. 当结构存在刚体位移时，如果没有约束或者约束不全，刚体的模态将被提取，其模态频率在0 Hz附近^[16]，该模态频率没有对比意义. 此外，3~6阶的固有频率非常相近，这是因为振动台模型具有对称性，所以出现了频率相近但方向不同的相似振型^[17].

从总体上来看，随着振动台固有频率的增加，其形变量也呈现逐渐增大的趋势. 在低频阶段，形变量增加的幅度最大，随着阶数的提高，形变量增加的幅度急剧下降. 就振动形变而言，主要发生在振动台的第三支撑立柱和部分固定挡块上，其他区域发生的形变相对较小，振动台的工作频率应避免处于42.10~45.47 Hz区间.

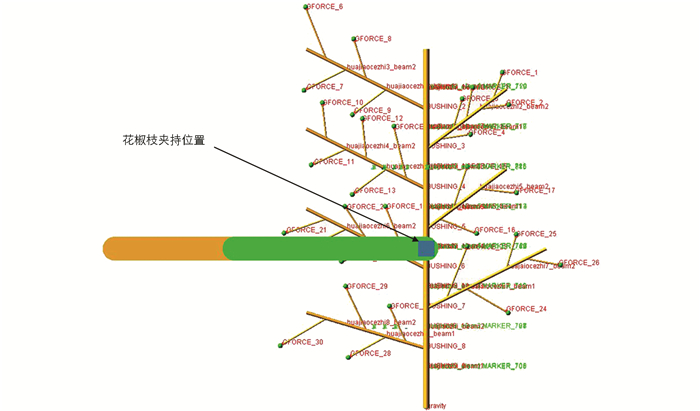
分别使用Excel和SPSS对仿真试验结果进行极差分析和方差分析，如表 6和表 7所示. 由极差分析可知，试验因子对花椒果脱落率的影响主次排序为：曲柄转速B、曲柄长度A、夹持高度C，最优组合为A₃B₃C₃，即曲柄长度250 mm、曲柄转速80π rad/s(对应振动频率40 Hz)、夹持高度300 mm. 该最优组合不属于表中组合，对该最优组合进行仿真试验验证，其夹持位置和振动后花椒果脱落情况如图 9所示. 经过仿真试验，花椒枝上30颗花椒果脱落29颗，脱落率为96.67%，脱落效果好，高于表中最优组合的脱落率. 由方差分析结果可知曲柄长度A和曲柄转速B影响显著，且曲柄转速B较曲柄长度A影响更为显著，夹持高度有一定影响，与极差分析结果吻合，与文献[18]结论一致.

1) 针对我国花椒采摘难、效率低、易伤手等问题，设计了基于下桩采摘法的振动式花椒采摘机，建立了花椒枝果柔性体模型，确定了花椒果振动脱落条件.

2) 振动台水平方向位移本质上是谐振动方程，对基于曲柄滑块机构的振动台进行模态分析，确定了其固有频率和振型. 为避免共振，振动台的工作频率应避开42.095~45.473 Hz区间.

3) 基于ADAMS虚拟正交试验表明，振动式花椒采摘机在振动频率40 Hz、曲柄长度250 mm、夹持高度为300 mm下脱果效率最佳，脱落率为96.67%.