建筑尺度可分为竖向尺度和水平尺度，竖向尺度指的是建筑高度，主要影响视觉感受，而水平尺度指的是建筑占地面积. 传统山地公园建筑的尺度控制多以感性描述为主. 在自然山水背景下，秦汉宫苑是将人工建筑散布于自然山水之中，追求弥山跨谷的气势；在写意山水理念中，则强调“东南移入户庭间”(白居易《累土山》). 二者尺度跨度巨大，却又在天人合一的自然山水观中完美融合^[6]. 吴亮^[7]在《止园集》中写道：“园亩五十而赢，水得十之四，土石三之，庐舍二之，竹树一支”. 陈从周^[8]在《说园》中提出：“风景区之建筑宜隐不宜显，宜散不宜聚，宜低不宜高，宜麓不宜顶”. 从这些文献中可以看出，传统山地公园建筑的尺度控制理念体现了朴素的生态观，强调的是建筑与自然环境的和谐融合.

目前针对山地公园建筑对生态环境影响的研究文献较少，而其中针对山地公园建筑水平尺度与生态环境关系的研究更是凤毛麟角，且多为定性研究. 大多数学者主要从形态、空间、景观、交通和技术等方面对山地建筑如何适应山地地形环境作了探索和研究. 卢济威等^[9]和张玉虎等^[10]从视觉、生态、情感和空间等方面探讨了山地建筑的设计要点. 夏晨曦^[11]则从建筑布局、形态表现及适宜性技术等方面提出适应自然山地地貌的山地公园建筑设计策略. 李保峰等^[12]则认为设计师若能从地形中发现自然力场的存在，将其作为设计的前文本，则“自然”就会成为建筑形态布局的秩序之源，建筑应充分融合于自然景观中，展现山地公园的生态特色，减少对山地环境的干扰^[13-14]. 陈烨等^[15]从参数化的角度对山地环境中的竖向因素进行建筑范围、坡形限高和体量轮廓3个方面进行了分析，提出了建筑边界度、地段包容度、建筑密度、坡形限高比、视觉高度比和视觉面积比等6个参数指标体系. 总体而言，大部分的研究都是从视觉景观及使用功能与山地地形的融合角度出发的.

在山地条件下营造风景建筑，除了关注其视觉效果和使用功能，更重要是要防止山地生态灾害的发生. 水和土是山地环境中最敏感的生态要素，山地建筑的水平尺度与山地水土流失密切相关. 而细沟侵蚀与土壤侵蚀是判断水土流失的两个重要指标. 本研究选择影响山地生态环境较大的两个因子——坡度与汇水面积，分别模拟计算得出不同坡度和不同汇水面积条件下建筑坡面长度与坡面流速、建筑占地面积与土壤侵蚀模数的对应数据. 再与坡面临界流速与土壤侵蚀模数分级标准相比较，来确定与判断建筑占坡面长度与占地面积的合理性，为山地公园中坡面建筑的水平尺度提供科学的计算方法与控制途径.

细沟侵蚀是指坡面地表径流不断增加，流速加快，产生强烈的坡面冲刷，在地表逐渐形成细小而密集的沟^[16]，是水土流失的重要表现^[17]. 建筑水平尺度对坡面流速的影响主要是因为不同的建筑坡面长度导致地表径流流经建筑场地时流速发生不同的变化，当坡面流速超过一定的临界流速后，对坡下地表将造成不同程度的细沟侵蚀. 在不同的建筑坡面长度条件下，对坡面流速与临界流速进行计算与比较，可以有效地确定不同环境条件下，合理的建筑坡面长度.

根据《开发建设项目水土保持技术规范》(GB 50433-2008)，坡面洪峰流量公式为：

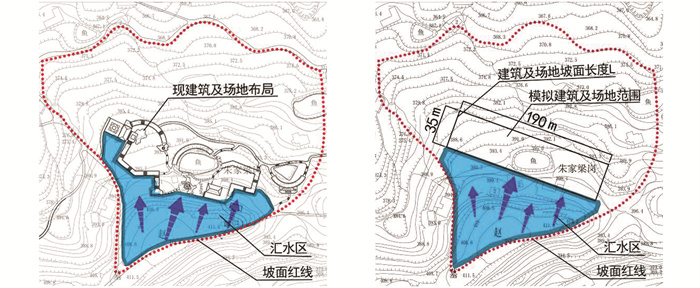
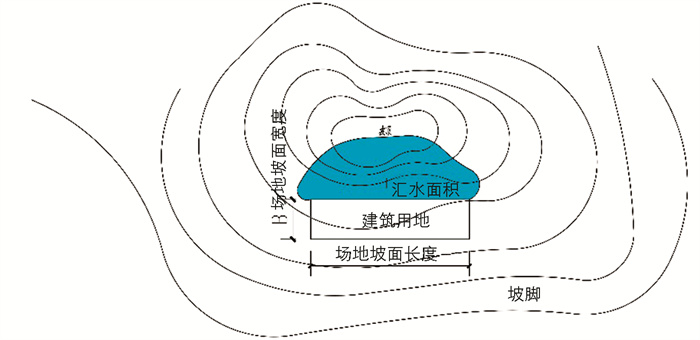
式中：Q_洪为相应洪水频率的最大洪水洪峰流量(m³/s)；K为径流系数；i为相应暴雨频率平均1 h降雨强度(mm/h)；A为集水面积(km²)，A=(L×B+F)(图 1)；通过计算坡面洪峰流量可以得到建筑单宽流量，其计算公式为：

式中：q为单宽流量(m²/s)；Q为坡面流量(m³/s)；K为径流系数；B为场地坡面宽度(m)；L为场地坡面长度(m)；F为上方汇水面积(m²)；I为相应暴雨频率平均1 h降雨强度(mm/h).

根据江忠善等^[18]的研究结果，坡面径流流速公式为：

式中：V为平均流速(m/s)；K为坡面阻力系数；J为坡比；m，n为流量与坡度的指数. (3)式为坡面平均流速通用形式，式中参数根据不同学者研究方法及地域条件而确定. 本研究采用张光辉^[19]的结果，K取23.66，m和n分别取0.246，0.542.

通过(3)式计算可得出：汇水面积相同、不同坡度和坡度相同、不同汇水面积的建筑坡面长度及坡面流速.

根据邵学军等^[20]的研究结果，坡面上细沟侵蚀发生临界速度为：

式中，v为临界速度，R为水力半径，J为坡比，g为重力加速度. 其中：

式中：n为曼宁糙率；k为超渗比率，可视为同等条件下裸地的径流系数；α为坡度；I₃₀为最大30 min雨强；L为坡长；J为坡比.

通过此公式计算可得出其他条件一致、不同坡度的细沟侵蚀临界速度. 坡度越大，临界流速越大，当坡面流速超过这些临界速度后，就会对下坡产生不同程度的细沟侵蚀.

土壤侵蚀是指土壤因地表径流、风力等外部作用下，被破坏、剥蚀、搬运和沉积的过程，土壤侵蚀量的大小是反应坡面生态稳定性的重要指标^[21]. 计算不同水平尺度的坡面建筑引起坡下土壤侵蚀量的大小与国家土壤侵蚀模数分级进行对比，从而确定对山地生态环境干扰合理的坡面建筑水平尺度.

基于RUSLE模型的重庆市土壤流失方程基本形式为：

式中：A为坡面侵蚀量(t/hm²)；R为降雨侵蚀力(MJ·mm·hm^-2·h^-1·a^-1)；K为土壤可蚀性(t· hm² ·h ·hm^-2·MJ^-1 ·mm^-1)；L和S为地形，其中L为坡长，S为坡度；C为植被覆盖度；P为水土保持措施. 各参数的计算方式如下.

(1) 降雨侵蚀力R. 本模型采用史东梅等^[22-23]等基于人工模拟降雨的手段建立的重庆地区降雨侵蚀力计算的年雨量模型：

式中：R_年为年降雨侵蚀力(MJ·mm·hm^-2·h^-1)；P_年为年降雨量(mm). 重庆市多年平均降雨量1 208 mm，多年平均径流深620.7 mm，多年平均径流总量511.4亿m³，由此计算，R取值为2 496.8.

(2) 土壤可蚀性K. 基于陈正发^[24]对于重庆市不同水土保持模式下的土壤可蚀性研究采用诺漠法估算重庆地区土壤可蚀性，其计算公式为：

式中：K_诺漠为土壤可蚀性；N₁=粉砂(0.05~0.1 mm)%+极细砂(0.002~0.05 mm)%；N₂=100-黏粒(＜0.002 mm)%或者为N₁+砂粒(0.1~2.0 mm)%；O_M为有机质的百分含量；S为土壤的结构参数；P为土壤的渗透级别. 根据本文的研究方向，选取陈正发^[24]对于重庆市不同水土保持模式下土壤理化性质及可蚀性K值研究，将场地按照梯平地模式取可蚀性K值为0.028，积累径流对下坡造成冲刷，原地貌按照水土保持林顺坡耕作模式取可蚀性K值为0.036.

(3) 地形LS. 本研究选用刘宝元等^[16]根据早期RUSLE中给出的地形因子LS进行的改进，建立了中国土壤流失方程CLSE.

式中：L为坡长；S为坡度；λ为坡长值；m为坡长指数；a为坡度，分别取10%，15%，20%，25%. 10%以下区域的坡度计算采用McCool^[25]等的公式，10%以上采用Liu等^[26]根据黄土高原陡坡情况改进的公式.

(4) 植被覆盖度C. 在USLE模型中，植被覆盖度C指在相同条件下的一定时间内，长有作物的标准小区与连续撂荒的标准小区上的土壤流失量之比. 在无实测C值时，可通过实测地表植被覆盖度，进而利用C值与植被覆盖度相关关系计算出C值来，采用蔡崇法等^[27]研究得到的公式：

式中，c为植被覆盖度，根据地块现状植被覆盖度进行取值，不同植被覆盖度对应不同取值，本研究根据现场调研经验取值50%.

(5) 水土保持措施P. P的取值根据陈正发^[24]对重庆及相似地区不同土地利用类型采用上述方法经转化、标准化后得到的水土保持措施P值表(表 1)取值，原地貌为林地取为0.037，场地径流积累冲刷下坡条件下设P值为1.

通过公式(1)-公式(11)可模拟计算出土壤类型、降雨强度与植被覆盖度相同时，不同坡度下不同建筑占地面积的平均土壤侵蚀模数，再与土壤侵蚀模数分级对比，可得出建筑占地面积大小与土壤侵蚀强度的对应关系，从而科学确定不同坡度下合理的建筑占地面积.

根据土壤侵蚀模数，采用土壤水力侵蚀强度分级标准(SL 190-2007)(表 2)，对坡地土壤侵蚀程度进行分级. 其中，重庆紫色丘陵区土壤侵蚀模数临界值为1 000 t/(km²·a)^[28]，超过此值将容易引起不同程度的土壤侵蚀，诱发生态问题.

选取重庆市渝北区照母山公园—照母山庄为模拟验证实例. 山庄位于公园北侧坡地，建筑占地面积6 500 m²，坡面总面积45 000 m²，上坡汇水面积8 000 m²，坡面总坡长231 m，建筑坡面长度约35 m，坡度约为20%；周边植被类型为林地，长势较好，覆盖度约50%；土壤类型为紫色土；基地多年平均降雨量1 208 mm，多年平均径流深620.7 mm.

选择原基地坡度20%，模拟10%，15%的坡度与基地8 000 m²，模拟10 000，15 000，20 000 m²的汇水面积分析建筑水平尺度对坡面流速的影响. 为了方便计算，根据照母山庄基地现状平面布局，将其模拟成长方形的规整场地(图 2). 根据坡面流速计算公式，模拟计算出照母山庄汇水面积不变，坡度分别为10%，15%和20%时的建筑坡面长度与坡面流速(表 3)；以及坡度不变，汇水面积分别为8 000，10 000，15 000，20 000 m²时的建筑坡面长度及坡面流速(表 4).

通过临界速度公式计算可得：坡度为10%，V值为12.38 cm/s；坡度为15%，V值为12.93 cm/s；坡度为20%，V值为13.45 cm/s. 坡度越大，临界流速越大，当坡面流速超过这些临界速度后，就会对下坡产生不同程度的细沟侵蚀.

根据坡面流速模拟计算结果(表 3和表 4)，使之与得到的细沟侵蚀临界速度进行对比，得出不同坡度、汇水面积下合理的建筑坡面长度(表 5). 从表 5可判断：照母山庄合理的建筑坡面长度应为30 m以内，这与照母山庄现状坡面长度一致，能满足生态要求.

钟壬琳等^[29]在紫色土坡面径流与侵蚀特征模拟试验研究中表明：在紫色土坡面径流总量有随坡度和雨强增加而增大的趋势，因此，坡度和降雨量是引起山地土壤侵蚀最重要的因子. 在本验证过程中，假设其他条件都不变，将坡度作为变量. 选择原基地坡度20%和模拟10%，15%，25%等4个坡度，分析建筑水平尺度对土壤侵蚀的影响. 通过土壤侵蚀模数的模拟计算，对照土壤侵蚀模数分级标准，可得出照母山庄在土壤类型、降雨强度与植被覆盖度相同、不同坡度下不同建筑占地面积对坡地土壤侵蚀强度(表 6).

参照重庆紫色丘陵区土壤侵蚀模数临界值，对比表 6与表 2可知：

坡度为10%时，建筑占地面积控制在2 000 m²以内，土壤侵蚀程度为微度，在土壤流失量的容许范围之内，面积在2 000~8 000 m²以内，会对坡地产生一定的生态干扰，但在适度干扰范围以内，面积大于8 000 m²后，会造成土壤侵蚀程度过大，破坏生态环境.

坡度为15%时，建筑占地面积4 000 m²以内，对坡地产生干扰在适度范围以内，面积大于4 000 m²后，对坡面土壤侵蚀模数超过可控范围，易造成水土流失；

坡度为20%和25%时，为了保证对生态干扰在适度范围以内，建筑及场地面积需要控制在2 000 m²以内，＞2 000 m²后，会造成坡下发生轻度、中度甚至强烈的侵蚀.

照母山庄基地现状坡度为20%，建筑及场地的面积为6 500 m²，平均土壤侵蚀模数约为1 500 t/(km²·a)，依据模拟计算结果，山庄将对坡下的生态环境产生较大影响. 但在实际调研过程中，照母山庄坡下生态环境比较良好，未发现水土流失现象. 究其原因是：一方面，因其不是纯粹的建筑硬质场地，由很多有机分散的林地、水体、花池和花坛等自然斑块有机嵌合形成，环境较为生态(图 3). 另一方面，照母山庄下坡种植很宽且密集的人工林带，减少雨水对坡面的冲刷，同时减少人为活动的干扰，起到了生态防护的作用.

建筑水平尺度大小与坡地的生态环境好坏呈正相关. 当建筑水平尺度适中，对山地干扰适度，将有益于形成良好的生态环境模式；当尺度过大，势必引起山地生态环境的变化，甚至发生土壤侵蚀、滑坡、崩塌等生态灾害，影响山地生态系统的稳定性. 因此，在山地公园建筑水平尺度控制时应首先考虑对山地生态问题的避免，再根据视觉美观、功能需求以及人的行为特征、心理特征等方面确定合理的建筑水平尺度.

坡度、汇水面积、植被覆盖度和土壤类型是影响山地公园生态环境的重要因素，在对山地公园坡面建筑水平尺度控制时，应充分考虑各区域坡度、汇水面积、植被覆盖度和土壤类型等因子条件，进行坡面流速与土壤侵蚀方面的科学计算，以确定合理的建筑水平尺度. 坡面流速分别与坡度、汇水面积、建筑坡面长度呈正相关，任何一个变量的增加都会引起坡面流速的加快；坡度、建筑占地面积与坡面平均土壤侵蚀模数呈正相关，坡度与建筑场地面积的增加都会引起平均土壤侵蚀模数增大.

在山地环境中，建筑如果需要承载特殊的使用功能或视觉美观需求，尺度需要适度扩大时，应充分考虑场地本身的生态性，可以通过采用覆土式建筑或在场地内部增加小型自然林地、花池和水体等自然斑块的形式增加斑块之间的连接度以及改变场地透水性，对雨水进行合理组织，以减少地表径流和土壤侵蚀.