-
开放科学(资源服务)标志码(OSID):

-
随着经济的发展,中国已经成为世界上最大的人力和物资流动国家,2010-2019年全国公路里程由400.82万公里增长到501.25万公里,年复合增长率为2.5%,交通问题已经成为影响社会发展的关键因素. 随着机动车数量日益增多,拥堵问题、交通事故、能耗问题、环境问题已经成为社会痛点问题. 因此,能够预测道路交通流量,并对道路进行实时疏导、路网规划建设有着至关重要的作用. 道路交通是一个复杂的系统,呈现出非线性、随机性和动态性的特征. 众多学者纷纷聚焦该领域,提出了许多预测方法. 比如宫同伟等[1]以新浪微博签到数据为基础,运用核密度分析法和分类统计法,揭示天津市轨交站区个体行为的时应变化特征,归纳轨交站区个体行为的空间聚集模式. Williams等[2]、李建森等[3]、李静娴等[4]提出了移动平均模型、回归模型等方法,而这些模型多是解决先行问题,针对道路交通的非线性系统预测效果不佳. 为了更好地模拟交通流量中的非线性时空问题,机器学习的方法被广泛应用其中,如支持向量机算法和神经网络算法. 姚智胜等[5]、朱永强等[6]、Toan等[7]、郑义彬等[8]提出了支持向量回归机的短时交通流量预测,然而当二次规划求解涉及到M阶矩阵的计算时,如果M(M是样本数量)很大,将耗费大量的机器内存和运算时间,在此基础上郭萌等[9]、罗山[10]、张帆[11]提出神经网络算法更适合于大数据非线性系统的预测. 但该模型也存在不足,比如收敛慢、易陷入局部最优. 针对这些问题,张健等[12]提出了增加动量项来提高收敛速度,但BP神经网络初始的权值和阈值是随机的,不同初始值对预测结果影响较大. 张春生等[13]、黄承锋等[14]、王小凡等[15]、黄富程等[16]采用遗传算法来优化BP神经网络的初始权值和阈值,通过选择、交叉和变异操作找到最优适应度值,再将得到的权值和阈值赋给BP神经网络,最后使用反向插播进行训练. 然而,遗传算法对初始种群依赖性较高,不同的初始种群预测结果也不同,因此很容易陷入局部极值. 蔡翠翠等[17]、董海等[18]、张德干等[19]采用粒子群算法来改进BP神经网络初始的权值和阈值,但同样局部寻优能力不足,算法易陷入早收敛.
交通流量的预测主要服务于道路协调管控和后期建设规划,如果仅仅以短时来定量预测流量值往往会造成在某个时段管控的频繁调整,且在交通流量预测过程中存在不定性、周期性、非线性的特点. 针对上述文献的不足,本文提出采用群体智能优化算法的麻雀优化算法来改进BP神经网络算法,以期达到高拟合度流量预测的目的. 本文所提方案主要工作有:①采用麻雀优化算法对BP神经网络算法的初始权值和阈值进行优化,降低局部最优概率,提高预测精度、收敛时效. ②根据交通的波动规律提出分组区间预测,不仅提高交通流量预测的准确性,并且波动区间可以实时调整,为智能交通流量预测提供更有利的信息.
全文HTML
-
群体智能优化算法是一种建立在概率理论基础上的随机搜索算法,主要模拟了生物群体在进化过程中独特的行为和生存方式,比如模拟昆虫、鸟群等群体的觅食行为,群体间通过某种合作方式去寻找食物,并且通过交流能够更快地得到更多的食物,从这类群体行为中抽象出的一种算法就称之为群体智能优化算法.
群体智能优化算法由Beni等[20]1989年首次提出,Colorni等[21]1991年提出蚁群算法,Smets等[22]1994年提出粒子群优化算法,开启了群体智能优化算法研究的热潮. 群体智能优化算法能够从全局上解决最优化问题,其去中心性的特点,使其在鲁棒性、自组织性、灵活性上受到越来越多的认可,近几年被广泛用于工程预测、图像检索和特征选择等领域. 目前常见的群体智能优化算法有蚁群优化算法、粒子优化算法、细菌觅食优化算法、布谷鸟优化算法、蝙蝠算法、灰狼优化算法、鲸鱼优化算法、骑手优化算、麻雀优化算法等.
李雅丽等[23]对上述优化算法进行比较,将单模态测试函数、多模态测试函数、固定维数的多模态基准函数等标准基准测试函数进行比较实验,从收敛速度、精度、稳定性等角度进行比较,提出的SSA优化算法各方面的性能都远超其他优化算法.
-
SSA优化算法又称麻雀搜索算法,是由Xue等[24]2020年提出的最新群体优化算法. 该算法主要受到麻雀觅食行为和反捕食行为的启发,具有优化能力强、收敛快、稳定性高的特点.
SSA优化算法模拟了麻雀在觅食活动中的3种角色行为. ①发现者,主要在群体活动中担任寻找食物的工作,由于拥有良好的能源储备且搜索范围广的优势,为种群觅食提供区域和方向. ②加入者,加入者跟随发现者一起活动,从中获取最好的食物以增加其能源储备值,同时加入者通过不断监控发现者并争取食物资源来增加其能源储备值,从而动态调整发现者和加入者的身份. 能量储备能力取决于麻雀个体适应度值的高低. ③警戒者,由加入者扮演,如果种群受到其他捕食者的威胁时,会发出鸣叫作为报警信号. 如果警报值高于安全值,发现者将加入者带到另一个安全区域进食. 一旦感应到危险,深处边缘的麻雀会迅速移动到安全区,同时占据更好的位置,而处于种群中间的群体会随机走动以便靠近其他麻雀.
由n只麻雀组成的种群用矩阵表示如式(1)所示.
那么,所有麻雀的适应度值可以表示如式(2)所示.
式(1)、式(2)中,d为优化问题的变量维数,n为麻雀种群数量,f表示适应度值. 在SSA算法中,拥有最好适应度值的发现者优先获取食物,并为加入者提供觅食方向. 因此,发现者获得的觅食范围要高于加入者. 随着个体适应度值的变化,麻雀角色也发生变化,在每次这样的迭代过程中,发现者的位置变化如式(3)所示.
式(3)中, Xi,jt+1表示第t次迭代后第i个麻雀个体的第j维位置信息(j∈{1,2,3,…,d}),itermax表示最大迭代次数,α为均匀随机数(范围为(0,1]),R2表示预警值(范围为[0, 1]),ST为安全值(范围为[0, 5, 1]),Q为随机数(服从正态分布),L是一个1×d矩阵(矩阵中的元素值均为1).
1) 当R2<ST时,意味着周围无捕食者,发现者可以进行大范围搜索以获得更多的食物.
2) 当R2≥ST时,意味着周围存在捕食者,同时向种群发出警报,所有麻雀会迅速飞到其他安全地方进行觅食.
加入者会跟随发现者去抢夺食物,并动态调整其适应值,其位置也会随着争夺食物而产生变化,加入者位置更新如式(4)所示.
式(4)中,t为迭代次数,Xp是当前发现者的最好位置,反之Xworst则是最坏位置. A是一个1×d矩阵(矩阵中的元素值为1和-1的随机数),同时矩阵A满足A+=AT(AAT)-1.
1) 当i>n/2时,意味着适应度较小的第i个加入者在本次搜索中未获得食物,自身处于饥饿状态,必须改变位置觅食.
2) 当i≤n/2时,意味着第i个加入者在最佳位置XP附近寻找食物的具体位置.
在模拟实验中,本文将警戒麻雀数量假设为总数的10%~20%,麻雀个体的初始位置随机,其算法表达式如式(5)所示.
式(5)中,Xbest是当前种群麻雀的最佳位置. β是服从正态分布随机数(β的均值为0,β的方差为1),β参数的作用是控制步长. K为随机数,其范围为[-1, 1],表示麻雀移动方向,也为步长控制参数. fi是当前第i只麻雀个体的适应度值. fg和fw分别代表当前种群麻雀的全局最高和最低的适应度值. ε是一个常数以避免分母为0.
1) 当fi>fg时,种群中的麻雀正处于边缘位置,极易受到捕食者猎杀.
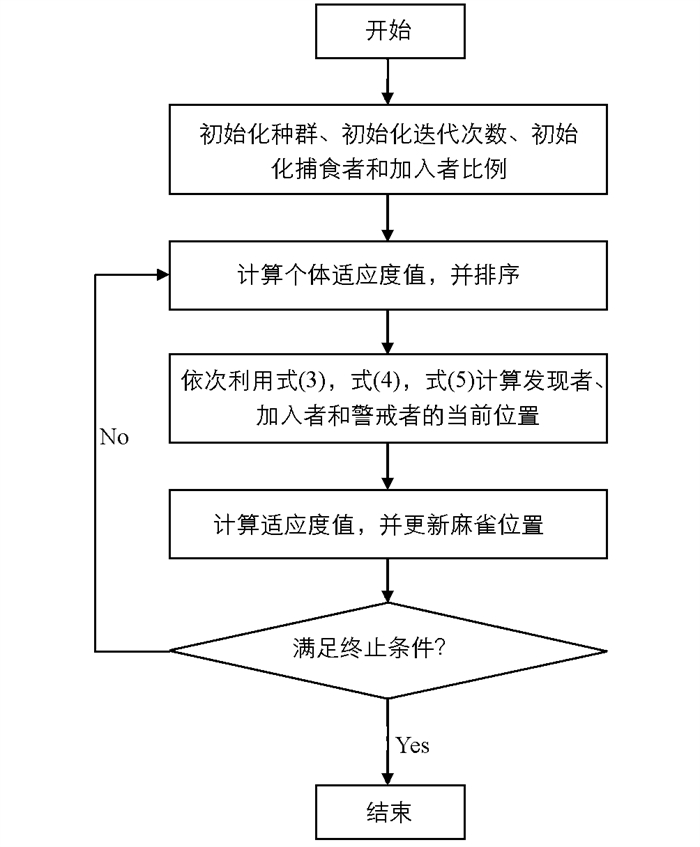
2) 当fi=fg时,种群中的麻雀已经感知到了危险临近,它们会通过靠近其他麻雀来减少被猎杀的风险. SSA优化算法流程如图 1所示.
-
BP神经网络算法是3层结构,即输入层、隐含层和输出层,它遵循“信息沿正向传播、误差沿反向纠正”的原则. 外部信息从输入层流入,经过每个隐含层神经元的加工和传递,最后由输出层输出信息处理结果,即完成信息的正向传播. 如果与实际输出不等,或者未达到允许的误差范围,则照“误差梯度下降”原则修正所有的权值和阈值. 可以进行多次正、反向传播的迭代直到误差减少到可接受的范围,或完成预定的学习次数即可.
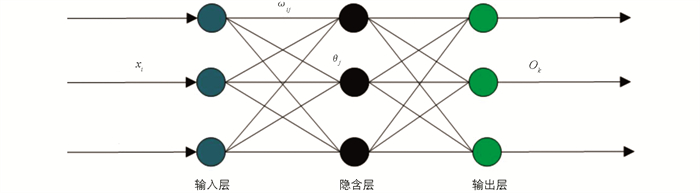
Rumelhart[25]1986年提出并证明了任何闭区间内的连续函数都可以用一个隐含层的BP网络来逼近,因此采用3层BP神经网络算法就可以完成n维到m维的映射,如图 2所示.
图 2中设输入层有i个节点(i=1,2…N),隐含层有j个节点(j=1,2…J),输出层有k个节点(k=1,2…K). 假设信息从输入节点i输入,其值为xi. ωij为神经元i到神经元j的权值,θj为神经元j的阈值,Ok为隐含层节点j的输出信息值. 那么,隐含层节点j的加权输入xj如式(6)所示,其实际输出Oj如式(7)所示. f(x)采用S型激活函数,隐含层选用非线性变化函数Sigmoid函数,其特点是函数及其导数都是连续的.
将隐含层节点的输出作为输出层的输入,隐含层第j个节点和输出层第k个节点连接的权值和阈值分别为ωjk和θk,可得第k个节点的输出Ok如式(8)所示.
若输出Ok与期望输出tk不符,可通过式(9)得出所有输出节点的训练误差.
通过不断地迭代调整各层的权值和阈值,迭代更新公式如式(10)所示,使得训练误差不断减少直至无限接近期望值,以期达到与期望输出无限接近的实际输出.
式(10)中,α为学习速率(α∈(0,1)),通过链式法则、Sigmoid函数导数特性可得输出层、隐含层的权值偏导如式(11)所示. 同理,也可求出各节点的阈值偏导.
BP神经网络算法通过反向修正权值和阈值将预测误差控制在允许范围内,实现了从输入到输出的映射. 数学理论已经证实3层BP神经网络算法能够以任意小的精度去无限逼近任何非线性连续系统,BP神经网络算法这一较强的非线性映射能力特别适用于解决内部机制复杂的系统. BP神经网络在训练时,自身能够通过学习提取出输入样本和输出样本之间的“规则”,并将学习内容存储于网络的权值中,体现出了高度的自学性和自适应性. 同时,在学习过程中若BP神经网络算法的局部神经元受到破坏,对结果不会造成较大影响,体现出了强大的容错能力和稳定性.
1.1. 群体智能优化算法
1.2. SSA优化算法
1.3. BP神经网络算法
-
BP神经网络算法的优点使其在不少应用中受到国内外学者的青睐,但是随着应用范围的扩大,BP神经网络算法也暴露出了许多不足. 如作为一种局部搜索的优化方法,对权值和阈值的初始取值敏感度高,不同的初始值往往会收敛于不同的局部极小,陷入局部最优的缺陷. 引入SSA算法后,利用其极高的寻优能力和高效的迭代收敛速度,在一定程度上提高了网络的非线性动态映射能力.
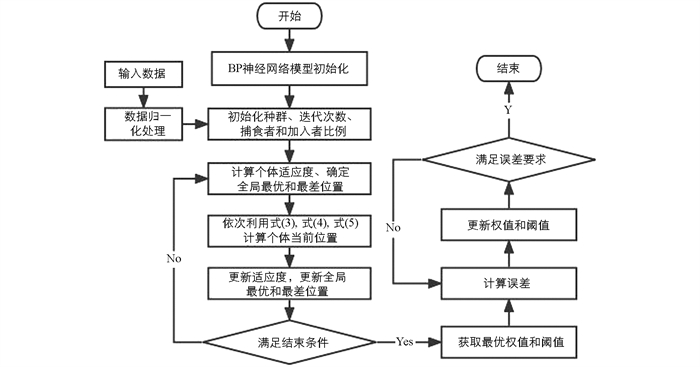
SSA-BP算法的基本思想是将BP神经网络算法的初始权值和阈值作为SSA算法的寻优目标,将预测算法中的均方误差作为SSA算法的适应度值,经过多次迭代将得到的结果赋值给BP神经网络算法,增强BP神经网络算法的寻优能力[26-27],其算法流程如图 3所示.
-
本文采用福州高速天龙山隧道入口的流量信息为实验数据. 采集2020年1月1日至2021年12月31日的数据信息,共计731条. 按照经验,路网流量波动一般以7 d为1个周期,输入为前7 d的车流量,输出为第8 d的车流量,取整数共计91组数据. 61组作为训练样本,30组作为测试样本.
-
本实验通过输入前7 d的车流量来预测第8 d的车流量,隐含层的神经元数量根据经验求出如式(12)所示[28].
式(12)中,h为BP神经网络算法中隐藏层神经元数量,n为BP神经网络算法中输入层神经元数量,k为BP神经网络算法中输出层神经元数量,a取1~10之间的任意值. BP神经网络算法中隐藏层的神经元数量在4~13之间选择. 经过实验,当网络隐含层节点数为11时,网络对测试样本具有最高的预测命中率. 因此,BP神经网络的结构是7-11-1. BP神经网络的训练次数固定在300;学习速率为0.01,目标误差为0.000 01.
-
为消除数据之间的量纲影响,对数据进行标准化处理. 本文通过min-max标准化处理,将结果映射到[0, 1]范围,转换公式如式(13)所示.
式(13)中,y为min-max标准化后的值,x为待处理的样本数据,ymin为min-max标准化后的最小值,ymax为min-max标准化后的最大值,xmin为待处理样本数据的最小值,xmax为待处理样本数据的最大值.
-
通过上述3层BP神经网络(7-11-1)算法计算网络的权值和阈值总量,计算方法如式(14)所示,得到优化的种群维度数dim=100.
初始麻雀种群数量为20,最大迭代次数为50,生产者占麻雀种群总量的20%,安全阈值ST∈[0.5,1](本文取0.8),警戒值R2∈[0, 1](本文取0.8).
MSE(Mean Squared Error,均方误差),是样本数据偏离真实值差值的平方和的平均数,也就是误差平方和的平均数,能够衡量样本数据与真实值之间的关系,MSE值越小,说明预测算法精度越高,预测值和真实值拟合度越高. 因此,采用均方误差作为SSA算法的个体适应度值,其计算公式如式(15)所示.
式(15)中,n为样本数,ci为预测值,yi为实际值.
2.1. SSA-BP算法建立
2.2. 实验数据及分析过程
2.2.1. 网络算法初始化
2.2.2. 数据预处理
2.2.3. SSA参数初始化
-
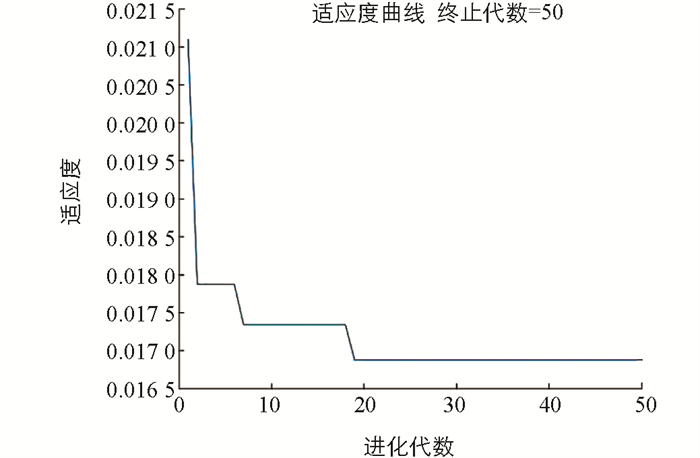
由图 4可见,经过50次迭代进化,适应度整体呈现出下降趋势,并在18次时达到最小值0.016 8,充分说明SSA算法能够用很小的开销来实现BP神经网络算法权值和阈值的初始值的优化.
-
从表 1可以看出,采用SSA-BP算法与传统的BP神经网络算法的最小相对误差值、最大相对误差值及均方误差值. SSA-BP算法的均方误差值为0.009 2,最小相对误差值为0.001 6,最大相对误差值为0.192 3,根据计量经济学中对评价算法的误差理论原理,将误差控制在20%范围内即为效果比较好的预测算法[29],通过比对可知本文的预测算法效果较好.
-
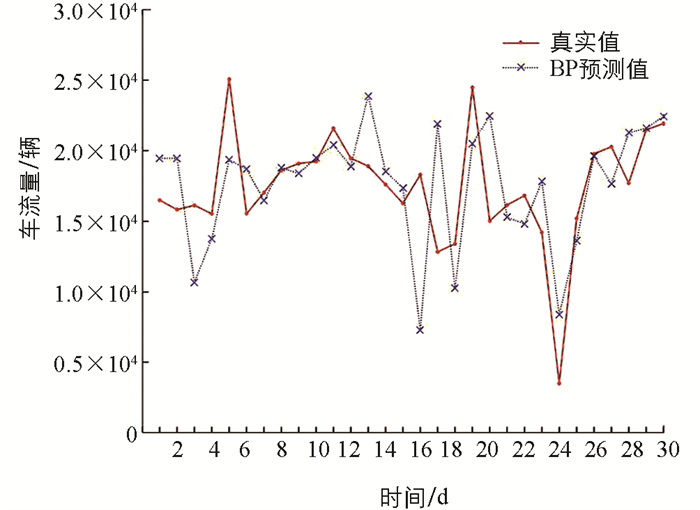
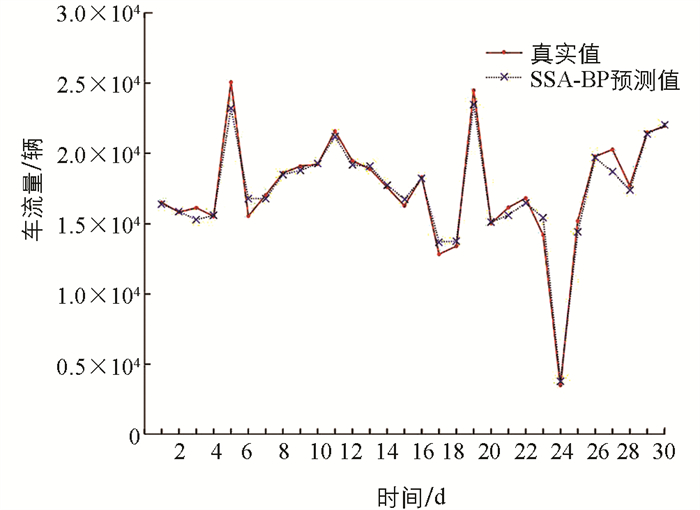
图 5、图 6分别为BP算法和SSA-BP算法的预测值与实际值对比图. 由图 6可知,SSA-BP算法的预测值与实际值对比曲线平稳,而传统BP神经网络算法的预测值与实际值对比曲线波动较大,并出现奇异点(图 5),说明采用传统BP神经网络算法在训练中易陷入局部最优的状态,从而导致测试结果出现误差偏离.
SSA-BP算法的拟合度值为0.970 4,BP算法的拟合度值为0.261 5. SSA-BP算法的拟合度值高于BP算法且趋近于1,说明样本特征的学习曲线较平滑,SSA-BP的算法泛化能力优于BP神经网络算法,训练过程中精确率逐渐提升,证明SSA-BP算法对传统BP神经网络算法进行优化有效且算法稳定性高,为交通流量区间预测提供了新的行之有效的解决方法.
3.1. 适应度变化
3.2. 误差比对
3.3. 拟合度比对
-
本文提出采用SSA-BP算法对交通流量进行预测,以前7 d的流量作为输入值,第8 d的流量作为输出值. 研究表明,SSA-BP算法在改进交通流量预测方面具有较大突破,能够有效地映射交通流量随时间变化的复杂非线性系统,具体表现在如下两个方面:
1) 利用SSA算法对BP神经网络算法的初始权值和阈值进行优化,改进了BP神经网络算法初始值随机性的问题,针对BP神经网络算法易陷入局部最优的问题,提出了一种新的解决方法.
2) 通过误差、拟合度的对比分析,证明了SSA-BP算法在预测精度、收敛速度、泛化能力和稳定性均强于BP神经网络算法,预测结果更适用于随时间变化的复杂非线性系统工程应用.



 下载:
下载: