-
目前PSO算法应用十分广泛[1-4].粒子群算法前期搜索容易导致收敛速度过快,在某些情况下随机振荡现象会对算法后期搜索产生较大的影响,容易限于局部极小值,搜索精度大大的降低,并且有时候还会导致算法的发散[5],对此衍生出了若干PSO新算法[6-15].
在研究了PSO算法以及各种衍生的PSO新算法以后,本文将学习与竞争思想引入到PSO算法中,构造一种新的PSO算法.
全文HTML
-
状态属性
其中xit表示粒子i在t时刻的位置,[Ld,Ud]表示xidt的取值范围.
其中vidt表示粒子i在t时刻的速度,[vmin,d,vmax,d]表示vidt的取值范围.则PSO算法迭代更新公式为:
式中:pidt和pgdt分别为当前个体和前种群最优值;r1,r2是均匀分布的随机数,区间范围为(0,1);c1,c2表示根据问题设定的学习因子.
-
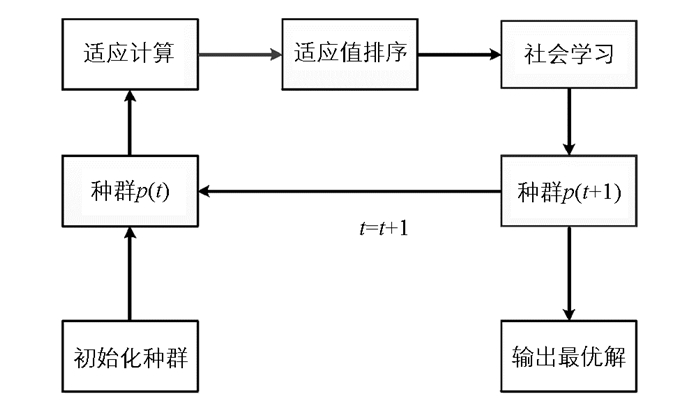
图 1是基于学习与竞争的PSO算法(简称LC-PSO算法)的主要过程,首先计算种群的所有个体的适应值,然后按照一定规则对种群个体适应值进行排序.
通过社会学习以后的修正项为
其中:Xi,j(t)表示在t代时j维向量的第i个粒子的状态,PiL表示第i个个体的学习概率.个体i会随机向比自己好的个体进行学习而不一定是向最优个体学习.
如图 2所示是LC-PSO算法中种群个体适应值排序过程,按由高到低的顺序从左到右排列.最左边的1表示适应值最好的个体,m表示当前种群中适应值最差的个体.依据社会学习的基本思想,种群中适应值差的个体向好的个体进行学习,则基于社会学习的PSO算法如式(6)所示:
其中r1(t),r2(t),r3(t)为0到1的随机数,
对式(6)分析可知,ΔXi,j(t+1)由3部分构成:第1部分为r1(t)ΔXi,j(t),与传统PSO相同;第2部分为r2(t)Ii,j(t),表示较差个体向较好个体学习的过程,具体为个体i向比自己好的个体k进行学习的结果;第3部分为r3(t)εCi,j(t),其中ε取值为较小的一个正数,依据是所求问题规模.这个部分表示的是种群的中心位置,这个部分的作用是对算法的收敛性进行控制.
1.1. PSO基础理论
1.2. 基于学习与竞争的改进PSO算法
-
本文提出的基于学习与竞争的改进PSO算法有3个参数需要确定,分别为个体学习概率PiL、种群的规模m和社会学习概率参数ε.在大量实验的前提下,给出了本文算法的参数选择规则.种群规模
其中:M表示的是本文算法中种群数量,n表示求解优化问题的维数.在经过大量的实验以后,本文选取M=100.
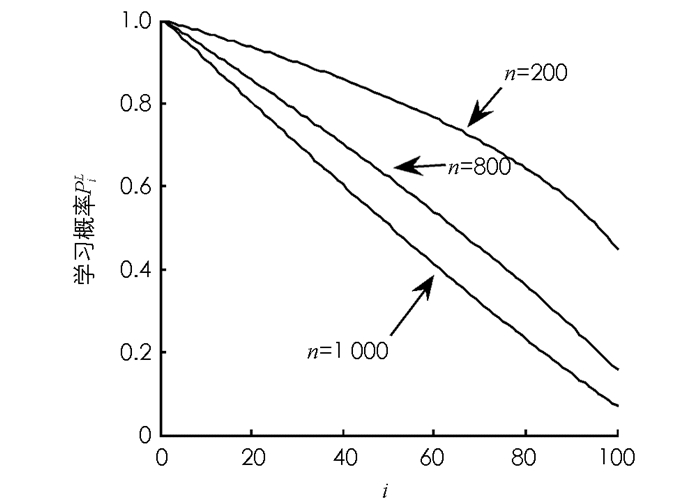
个体学习概率PiL对本文算法有着至关重要的影响作用,适应值差的个体以学习概率PiL向适应值好的个体学习,求解优化问题的困难程度与学习过程的困难程度成正比,基于以上知识,在式(11)中给出了PiL的表达式:
从(11)式可得出PiL和i成反比关系,这反映了种群中适应值越好的个体作为被学习对象的可能性越大;还可得出学习概率PiL与问题规模n成反比关系,这反映了问题的规模越大则学习的速度越慢.这样的法则能够保持该算法种群的多样性.一般要求α < 1,在本文中选取α=0.5.
ε是用来控制算法迭代公式(6)中r3(t)εCi,j(t)的取值.通过大量实验给出ε的表达式:
其中β是一个较小的正数,本文取β=0.01.由(12)式可以得出:问题规模与ε成正比关系,而种群规模则与ε成反比关系.
-
当PSO算法种群内部所有个体完全相同,即种群不会再依据算法的迭代法则发生变化则认为该算法收敛.根据改进PSO算法的迭代公式有:
假设式(6)和式(7)中的随机数有确定的期望值.对式(6)进行替换可以得到:
令
$ \theta = \frac{{1 + \varepsilon }}{2}, p = \frac{1}{{1 + \varepsilon }}{X_{k, j}}(t) + \frac{\varepsilon }{{1 + \varepsilon }}{\bar X_{i, j}}(t)$ 带入到式(11)中可得:PSO算法的寻优过程可以看做是一个动态系统变化的过程.
结合(16)式有
矩阵A在动态系统中称为状态矩阵,B称为输出矩阵.这个动态系统能否收敛是由矩阵A的特征值λ所决定的:
由此可以得到矩阵A的特征值为:
该系统收敛的充分必要条件是矩阵A的特征值小于1,即|λ2| < 1,由此可得
在PSO算法中n,M,β一般都取大于0的常数,所以以上表达式都成立.由此可知改进的PSO算法依然满足动态系统收敛的充分必要条件,所以该算法收敛.
-
采用7个测试函数进行仿真实验:
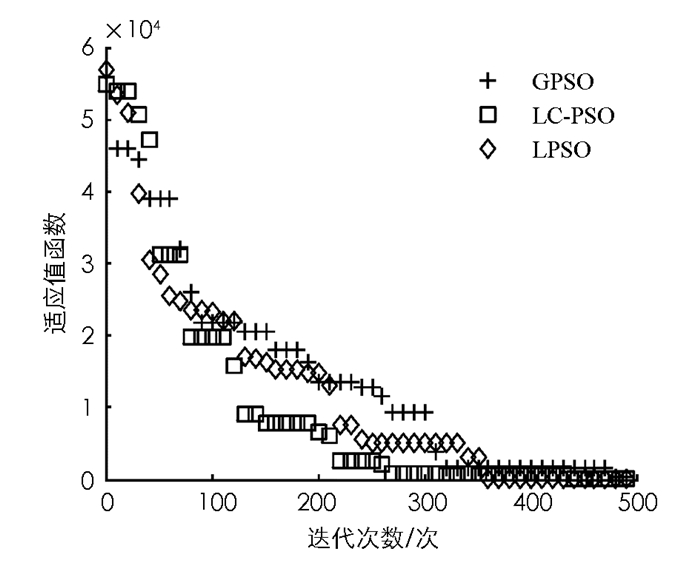
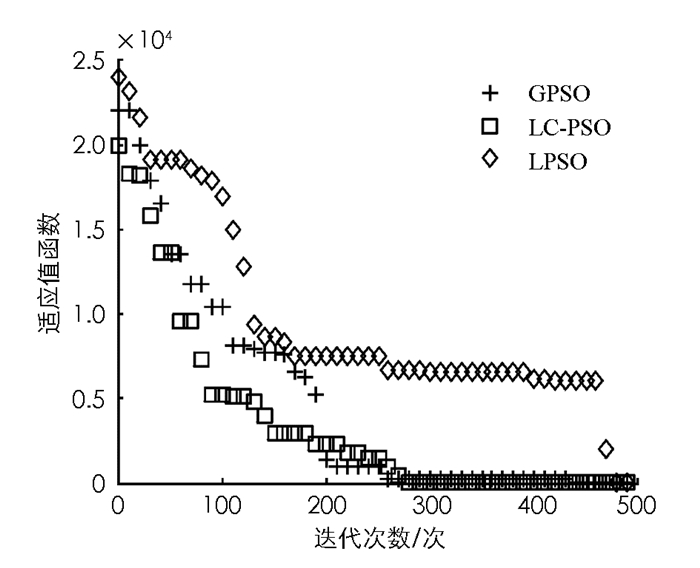
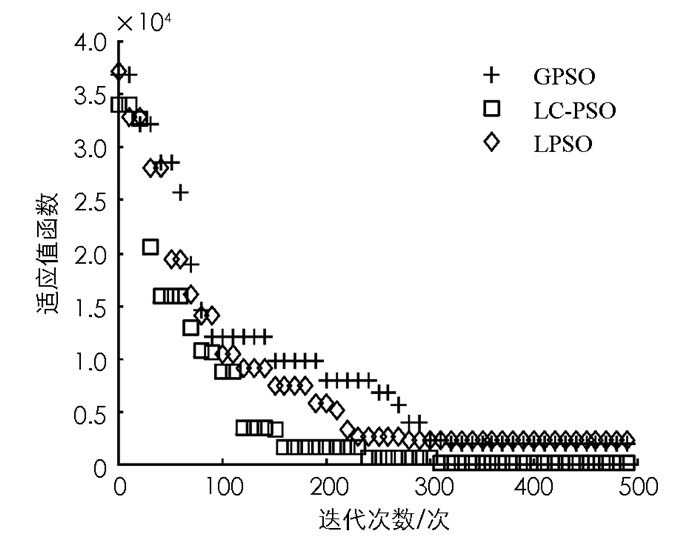
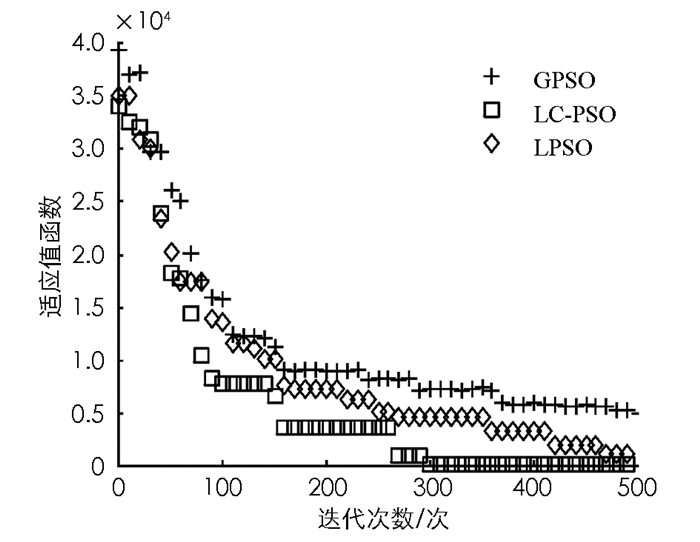
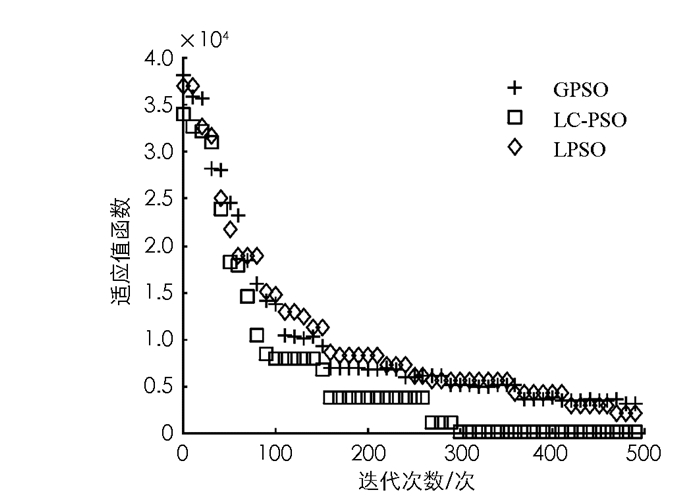
表 1为每个对应的测试函数的自变量搜索范围;表 2为本文LC-PSO算法与目前常规的2种改进PSO算法(LPSO和GPSO算法)的参数设定.将每种算法运行200次,给出每种算法求解结果的平均值(表 3).对比3种算法的求解结果发现,相对于以往的PSO改进算法,本文提出的LC-PSO算法是求解精度最高的一种算法,即使面对复杂的函数优化问题也能够较好求出次优解.同时由表 4可知,LC-PSO的计算时间总体上要小于其它两种改进的PSO算法.这是由于与以往的改进算法相比,LC-PSO算法在迭代公式的设计上并没有增加自适应参数或者混合算法的过程,仅仅是通过学习与竞争的机制来体现种群的进化过程. 3种算法迭代过程的变化图如图 4-10所示.
由图 4-10可知本文所给出的基于学习与竞争的改进PSO算法(LC-PSO)收敛速度更快,计算结果更准确.
另外为了证明本文算法的优越性,将本文算法与改进遗传算法(GA)[16]进行对比实验.求解问题为非线性约束的二元函数优化问题,数学模型为:
其中:13≤x≤100,0≤y≤100.已知全局最优解为(x,y)=(14.095,0.842 96),F(x,y)=-6 961.813 381.实验结果见表 5.
由表 5中数据可知本文算法在求解精度和时间性能方面都优于改进GA算法.
4.1. 测试函数
-
本文提出了一种基于学习与竞争的粒子群算法(LC-PSO).将学习和竞争的机制与基本的PSO算法结合,让种群中适应值差的个体来学习适应值好的个体,同时好的个体和差的个体之间相互竞争,由此替代了基本PSO算法的迭代公式,构成了新的PSO算法.该算法在提高搜索精度和寻优能力的同时并没有增大算法的计算量.该改进算法求解函数优化问题收敛速度更快,计算结果更准确.



 下载:
下载: