-
边缘提取是图像分析中的一个重要研究领域[1-3].由于边缘与噪声均为高频信息,消除噪声时也很可能消除一部分边缘,所以噪声抑制与边缘确定一般很难同时兼顾.因此,边缘提取需要同时处理好噪声抑制与边缘保持的问题[3].常用的如Laplace,LOG,Sobel等边缘提取算法虽然操作简单,但抗噪性弱、性能稳定性不强,得到的边缘清晰度和完整性还需提高[4].文献[5]定义了一种基于局部二值模式(Local Binary Pattern,LBP)的图像边缘检测技术,但由于LBP对噪声敏感、对光照变化稳定性弱,因此,当噪声存在时,出现了较多的伪边缘、弱边缘.文献[6]设计了一种改进的Canny图像边缘提取方案,一般噪声的抗干扰能力较好,但是当噪声强度较大时,边缘提取性能大大降低,易导致误判边缘的问题.文献[7]设计了一种基于WT与SVD的边缘提取技术,能在噪声图像中获取清晰的边缘,但是容易出现间断、不连续的边缘.
为了降低在边缘提取过程中噪声的敏感性,同时处理好噪声消除和边缘保持的问题,提高边缘的清晰度、连续性、准确性,增加边缘提取算法的适用性与稳定性,本文基于LBP理论,设计了一种改良LBP耦合蚁群优化(Ant Colony Optimization,ACO)边缘提取方案. LBP计算简单,且具有旋转不变性和均匀不变性等优点,但是其对噪声较敏感.为了克服LBP的不足,提高边缘定位精度,本文在LBP中嵌入一个S函数,定义了一种改进的LBP算子,能够较好反映像素间的差异程度,有效表示边缘的细微变化,并进一步引入ACO对算法进行了优化.
全文HTML
-
局部二值模式(Local Binary Pattern,LBP)是一种有效的纹理描述方法[8-9].定义一个3×3的范围,将与中心点相邻的8个点的灰度值与中心点比较,若相邻点的灰度值小于中心点灰度值,那么该点设定为0,反之为1,由此便生成了一个8位的二进制码.对此,可获得该窗口的LBP特征值,表示为[10]:
其中:gi是相邻点灰度值,gC是中心点灰度值,P是相邻点的个数,R是半径.
得到所有点(i,j)的LBP特征值后,将所有像素点(i,j)的LBP构建成一个直方图,表示为:
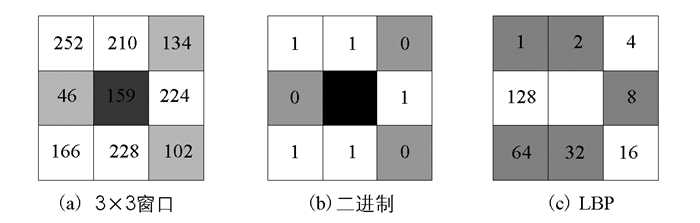
其中LLBP(i,j)为当前点(i,j)的LBP值. 图 1表示了一个3×3尺寸大小的LBP生成过程. 图 1(a)展示了3×3窗口中每个像素点的灰度值,中心点为黑色,灰度值小于中心点的为灰色显示.根据公式(1)与(2),灰色点转换为图 1(b)中的0,其他点显示为1. 图 1(c)为(b)对应的二进制数转换. LBP=1+2+8+32+64=107.
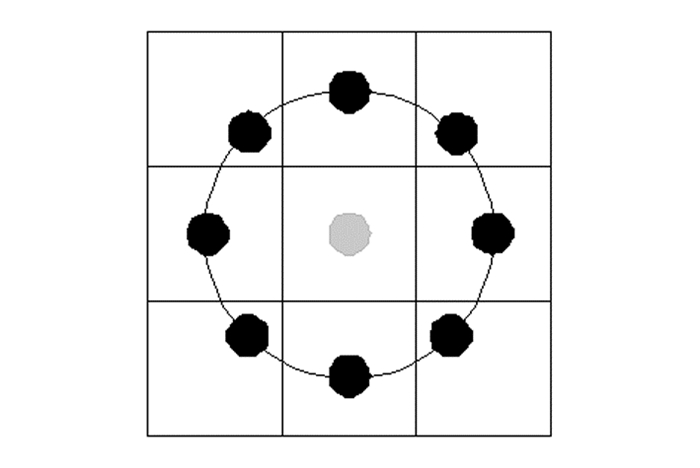
为了提高LBP的适用性,将图 1模型扩展成为一个圆形区域(图 2).该区域内的像素点P=8,半径R=1,再计算其LBP值.
通过式(1)知,LBP可获得2P种二进制编码.如果某个区域进行了旋转,那么以中心点为圆心,半径为R的区域内的P个点的gi也会产生变化,得到的LBP值也会相应产生变化.因此,针对该问题,需要对圆形区域旋转变换,计算其最小的LBP值,定义如下:
其中:RO(x,l)为旋转方程;l为旋转数量.因此,通过计算旋转变换的LBP最小值,可使其具有旋转不变性.
在LBP计算过程中,经常会产生一些特殊的LBP值,这些特殊的LBP一般含有重要的信息,能够表示丰富的细节和纹理[11].因此,为了反映LBP的均匀性,可表示为:
其中U为LBP中周围点的0与1间变换的数量,定义为:
U可作为纹理评价指标,U越小越均匀;反之,越大表示其越不均匀.一个(P,R)区域的LBP包括的均匀数量为P(P-1)+2.对此,均匀LBP的特征度显著降低,可在多尺度广泛适用.
为了提高LBP的性能,降低计算复杂性,设计了一种具有旋转-均匀不变性的LBP表示LLBPP,Rmu.将旋转不变LBP分成旋转-均匀不变和非均匀两种.其中,旋转-均匀不变共有P+1组,非均匀设为1组.所以,LLBPP,Rmu的特征维数为P+2.因此,LLBPP,Rmu降低了特征维度,在保持了纹理检测的同时具备了旋转不变性与灰度尺度不变性.
-
为了提高边缘提取算法的性能,减少噪音和模糊的影响,本文在LBP的基础上,设计了一种改进的LBP算法,通过嵌入一个平滑方程S,称之为SLBP.首先,为了降低噪声的干扰,对输入图像进行均值滤波处理,计算图像的SLBP特征值与权重.然后再将当前像素的SLBP值和前一个像素判断是否为非零,如果是,那么设置当前像素为白色,突出边缘,否则继续返回到上一步.为了进一步提高边缘的清晰度,降低伪边缘和弱边缘,引入了蚁群优化算法.本文设计的算法结构如图 3所示.
-
为了降低对噪声的敏感性,对式(1)进行演变如下:
其中:gi是相邻点灰度值;gc是当前点灰度值;f(x)为比较函数;T为冗余灰度变化的阈值,用于消除孤立点,从而选择光滑区域的点.
LBP算子对边缘特征的描述能力不理想.为此,引入一个平滑函数S来增强其描述能力,定义如下:
将S嵌入到比较函数f(x)中可得:
其中:
$d=\frac{\left(g_{i}-g_{c}\right)^{2}}{g_{i}+g_{c}}$ 反映了周围的点和中心点间的相似距离,d越小,两个像素点越相似;T是一个阈值,可以过滤多余的细微变化,以保证边缘的准确提取.根据式(10)得出,当两个像素点的相似差异大于T时,S单调减少,可较好减少白色线条的产生.S函数值按“单调”递增的顺序排序,因此,较大的S函数值其权重也较大,表示如下:
其中F为单调排序运算符.
通过在LBP中嵌入一个平滑函数S,得到一个新的SLBP,定义如下:
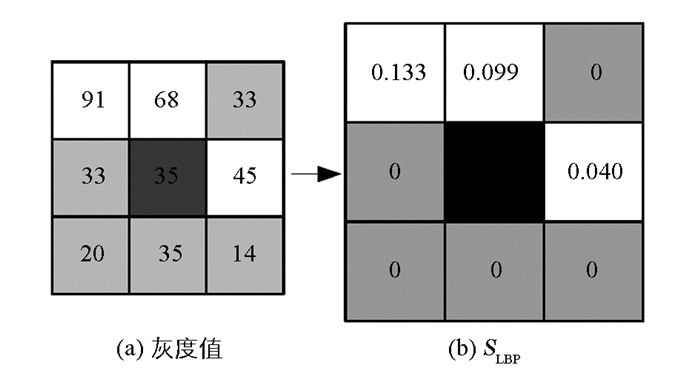
T的目的是为了消除孤立的噪声点. T=0时,为孤立噪声;T=8时,为孤立点或者为平滑区的点.通过改进,当gi与gc的差异程度不同时,得到的结果也不一样. 图 4所示为一个3×3窗口的SLBP.图 4(a)给出了3×3窗口中每个像素的灰度值;图 4(b)为与中心像素的SLBP比较所得结果,SLBP的值为24.
-
为了进一步提高边缘提取效率,通过蚁群优化算法(ACO)对边缘进行优化. ACO将图像看作2维空间,一个像素当作一个节点[12].本文ACO的边缘优化包括4个步骤:
1) 初始化.对于图像I,选取尺寸为M1×M2的区域的k个像素,蚂蚁随机处于像素上,设每个像素矩阵T n的初始值为T0.
2) 路径构造.由于不同点对蚂蚁的吸引力不一样,在第n次运动时,蚂蚁可选取的不同路线的概率可表示为[13]
其中:
$\mathit{P}_{(\mathit{l},\mathit{m}),(\mathit{i},\mathit{j})}^\mathit{n}$ 为从点(i,j)到(l,m)的概率;Ti.j,ηi,j分别为点(i,j)的强度与启发信息;ωΔ是权值函数,Δ为蚂蚁运动的方向变量,$\mathit{\Delta } = 0,\frac{\pi }{4},\frac{\pi }{2},\frac{3}{4}\pi $ ,Δ越大,ωΔ越小;α,β分别为强度和启发信息的控制参数.3) 信息素更新.通过每次运动后,信息素将按下式更新:
其中ρ为控制Ti,jn-1的变化参数.通过全部蚂蚁的运动,得到的像素矩阵为
其中:ξ是像素衰变值;T (0)是像素矩阵的初始值.根据步骤2)与3)的N次更新,得到新的像素矩阵T (n).
4) 边缘检测与优化.为了准确判别像素点,在T(n)中引入阈值τ[14].设初始阈值τ0,通过T(n)和τ0的大小关系可将像素分为G1与G2两部分:G1满足T(n)>τ0,G2满足T(n)<τ0.分别测量G1与G2的平均数
$\tilde{\omega}_{1}$ 和$\tilde{\omega}_{2}$ ,然后通过$\tilde{\omega}_{1}$ 和$\tilde{\omega}_{2}$ 计算新的τ,定义为不断迭代运算,直到τ小于预设值为止,通过路径优化与正负反馈求取边缘最优值.
由于本文算法构建的SLBP算子能够根据权重来精确计算像素间的差异程度,并且利用蚁群优化算法提高性能,从而准确提取区域边缘像素,不仅对图像中的单一目标具有较好的检测效果,而且对多目标的边缘提取仍然有效.
2.1. 改进的LBP
2.2. 蚁群优化算法
-
硬件环境为:Intel I3 3.50 GHz四核CPU,8 GB内存,500 GB RAM.软件环境为:Win7操作系统,MATLAB 2012.选择3种常见算法进行对比实验:基于LBP的边缘提取算法[5]、基于Canny的边缘提取算法[6]、基于WT与SVD的边缘提取算法[7].根据文献[6]与文献[12],预设τ=0.05,Canny算法中的阈值设为0.03,滤波窗口大小为3×3.
-
为了客观地对实验提取的边缘进行评价,将优质系数Pτ与边缘连续性R作为算法性能的衡量指标[15]. Pτ的值越大,说明边缘越清晰,细节越详细,表达式为
其中:no和nd为完整与实际边缘上的像素点;di为第i点边缘与完整边缘的距离.
边缘连续性R越大,表示边缘连续性越好、越完整,其表达式为[16]
其中:CEN为连续像素数量,TEN为总像素数量.
-
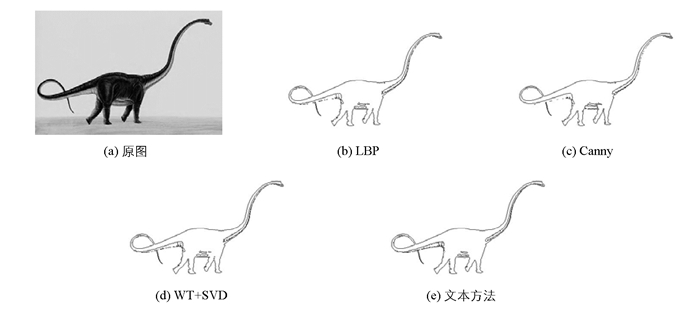
图 5(a)为无噪声的输入恐龙图像,图 5(b)-(e)分别为基于LBP方法、基于Canny方法、WT+SVD方法以及本文设计方法得到的提取结果.从图 5中看出,在不含噪声的恐龙图像中,4种方法得到的边缘整体均比较理想,能够较好得到恐龙的轮廓.但是,LBP与Canny方法得到的边缘产生了细碎的边缘;WT+SVD方法在恐龙腿部位置出现了局部断裂和繁琐边缘;本文方法的边缘较清晰、连续性好,准确表示了图像的结构与细节信息.
图 6为复杂的图像边缘提取结果.从图 6可知,本文算法对复杂图像的边缘检测同样具有良好性能,能够清晰显示细节信息.而其他算法效果不佳,出现了一些弱边缘与边缘漏检现象.
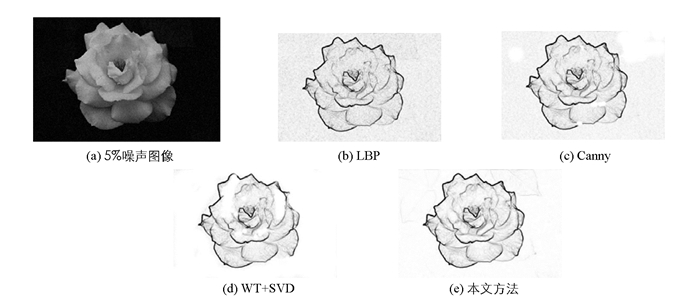
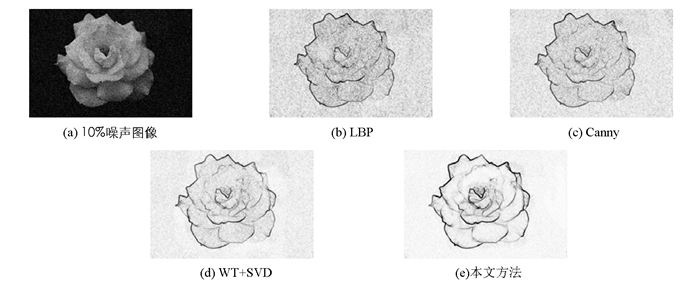
为了验证算法的抗噪性,借助PS CS3软件对图像加入不同密度的椒盐噪声后进行边缘提取实验,实验结果见图 7,8. 图 7(a)为添加5%密度噪声的花朵图像.由图 7可知,在噪声密度较低(5%)时,图 7(b)中的边缘提取效果不佳,出现了较多的噪声点,图 7(b)-(e)比较理想,能够反映花朵的轮廓和结构,特别是本文方法得到的边缘相对更清晰,无伪边缘与弱边缘,能够表现叶子等部位的细节信息.
图 8(a)为添加20%密度噪声的花朵图.由图 8可知,图 8(b)产生了很多虚假边缘和噪声点;图 8(c)产生了较多的伪边缘、噪声点,得到的边缘失真,细节信息模糊;图 8(d)出现边缘间断、不连续的问题;图 8(e)得到的边缘完整,边缘定位较高.
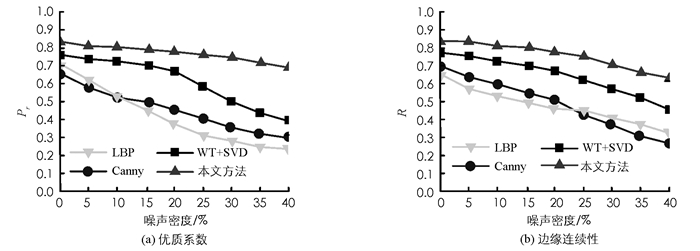
为了进一步测验算法的抗噪性,通过在图像中加入不同密度的椒盐噪声(5%,10%,…,40%),再分别利用4种算法在不同的噪声密度下对边缘进行提取.为了定量分析所得边缘的质量,通过测量优质系数Pτ与边缘连续性R,获得了不同噪声下的曲线图(图 9).从图 9可看出,本文方法的Pτ与R曲线相对较平稳,且在相同噪声下测量的Pτ与R最高.当噪声变大时,得到的Pτ与R曲线也随之降低,但是本文方法下降相对平缓,而其它3种方法波动较大.
本文算法除了对椒盐噪声具有良好的边缘提取效果之外,对其他类型的噪声干扰同样有效,因为本文在传统的LBP算子中引入平滑函数S从而可准确计算像素间差异,过滤多余的细微变化,保证了边缘提取的准确性与完整性.
3.1. 评价指标
3.2. 实验结果与分析
-
为了解决噪声消除和边缘保持的矛盾,提高边缘的清晰度、连续性,本文设计了一种改进的LBP耦合ACO图像边缘提取算法.实验结果表明,本文提出的S-LBP方法能够有效提高边缘提取的性能,得到的边缘清晰,连续性较好.



 下载:
下载: