-
1960年,Auslander和Bridger在双边noetherian环R上引入了有限生成模G-维数的概念.文献[1]推广了Auslander和Bridger的想法,在任意的环R上定义了Gorenstein投射模的概念.文献[2]证明了在noetherian环R上的有限生成R-模M是Gorenstein投射模当且仅当M是G-维数为0的模,发现了Gorenstein投射模有许多投射模的性质.文献[3]引入了Gorenstein投射模和Gorenstein内射模的两种特殊情况,分别叫做强Gorenstein平坦模和Gorenstein FP-内射模,这两种模的类在凝聚环上有许多性质类似于在noetherian环上Gorenstein投射模和Gorenstein内射模的性质.文献[4]重新命名强Gorenstein平坦模是Ding投射模,Gorenstein FP-内射模是Ding内射模.由文献[5]的命题10.2.6知,有限表示模M是Ding投射模当且仅当在左完全环上,M是Gorenstein投射模,Gorenstein投射模是Ding投射模.因此,由文献[4]的推论4.6知,在Gorenstein环上,Gorenstein投射模是Ding投射模.
利用有限生成投射模,文献[2]引入并研究了f-投射模. Gorenstein投射模是投射模的一类重要推广,文献[6]利用有限生成Gorenstein投射模引入了Gorenstein f-投射模. Ding投射模是Gorenstein投射模的一种特殊情形.受以上工作的启发,我们引入了Ding f-投射模的概念.
我们给出了Ding f-投射模的刻画,证明了:由所有Ding f-投射模左R-模的类关于直和以及直和项封闭;若R是左凝聚环,则由所有Ding f-投射左R-模构成的类关于纯扩张以及纯子模封闭.
本文中的R是带有单位元的结合环,所有模都是酉模.对左R-模M,M**表示对偶模HomR(M,R),δM:M→M**是自然赋值映射.
由文献[10]知,如果存在投射模的正合序列
使得M$ \cong $Ker(P0→P1),且对任意平坦左R-模F,有HomR(P,F)是正合的,则左R-模M是Ding投射模.
下面我们引入Ding f-投射模的定义.
定义1 如果对任意左R-模,同态f:A→M都可以通过有限生成Ding投射模左R-模P分解,则左R-模M是Ding f-投射模,其中A是有限生成左R-模.
等价地,对M的任意有限生成子模N,包含映射f:N→M可以通过有限生成Ding投射左R-模P分解.
命题1 有限生成左R-模M是Ding f-投射模当且仅当M是Ding投射模.
证 必要性 设有限生成左R-模M是Ding f-投射模.则恒等映射1M:M→M可以通过有限生成Ding投射左R-模D分解成g:M→D和h:D→M使得hg=1M.因此M是D的直和项.故M是Ding投射模.
充分性 设M是有限生成Ding投射模.则有限生成左R-模N到M的同态f可以通过有限生成Ding投射左R-模M分解.故M是Ding f-投射模.
记Γ={Di:i∈I}是有限生成Ding投射左R-模同构类的代表半单无赘集,且设
设A,B是左R-模.则对任意f∈HomR(A,⊕i∈IDi),g∈HomR(⊕i∈IDi,B),其中a∈A,有自然同态
其中
引理1 设B是左R-模,则以下结论等价:
(ⅰ) B是Ding f-投射模;
(ⅱ)对任意有限生成左R-模A,σA,B是满同态.
证 (ⅰ)$\Rightarrow $(ⅱ)设α∈HomR(A,B).因为B是Ding f-投射模,所以α可以通过有限生成Ding投射左R-模Dk∈Γ分解.存在β:A→Gk和γ:Gk→B,使得α=γβ.设π:⊕i∈IDi→Dk是标准投射,且λ:Dk→⊕i∈IDi是标准内射.取
因为α=σA,B(f⊗g),所以σA,B是满同态.
(ⅱ)$\Rightarrow $(ⅰ)设A是有限生成左R-模,且φ∈HomR(A,B).则存在
使得
因为A是有限生成的,所以存在有限指标集J⊆I,使得
定义ψ:A→(⊕j∈JDj)n为
且ξ:→(⊕j∈JDj)n B为
则φ=ξψ.因为(⊕j∈JDj)n是有限生成Ding投射模,所以B是Ding f-投射模.
由文献[5]知,如果对任意有限表示模F,序列${\rm{Ho}}{{\rm{m}}_R}(F, B)\mathop \to \limits^{{\beta ^*}} {\rm{Ho}}{{\rm{m}}_R}(F, C) \to 0$是正合的,则正合序列$0 \to A\mathop \to \limits^a B\mathop \to \limits^\beta C \to 0$是纯的.
下面给出本文的主要结果.
定理1 由所有Ding f-投射左R-模构成的类关于直和以及直和项封闭,若R是左凝聚环,则由所有Ding f-投射左R-模构成的类关于纯扩张以及纯子模封闭.
证 设(Mj)j∈J是一族Ding f-投射左R-模,Q是有限生成左R-模.对任意同态f:Q→⊕j∈JMj,因为Q是有限生成的,所以存在有限指标集K⊆J,使得Im(f)⊆⊕k∈KMk.由引理1知
正合.因此可以得到图 1.
因为下行正合,所以σQ,⊕k∈KMk是满同态.由引理1知,⊕k∈KMK是Ding f-投射模.定义τ:Q→⊕k∈KMK,使得对任意χ∈Q,τ(χ)=f(χ).则τ可以通过有限生成Ding投射模Z分解成μ:Q→Z和υ:Z→⊕k∈KMk,使得τ=υμ.设ι:⊕k∈KMK→⊕j∈JMj是包含映射,则f=ιτ=(ιν)μ.因此⊕j∈JMj是Ding f-投射模.故由所有Ding f-投射左R-模构成的类关于直和封闭.
设U是Ding f-投射左R-模V的直和项.定义π:V→U是标准投射,i:U→V是标准嵌入.对任意有限生成左R-模X和任意同态α:X→U,存在有限生成Ding投射左R-模Y,β:X→Y和γ:Y V,使得iα=γβ,则
因此U是Ding f-投射模.故由所有Ding f-投射左R-模构成的类关于直和项封闭.
设R是左凝聚环,且0→A→B C→0是左R-模的纯正合序列.假设A和C是Ding f-投射左R-模.因为Di∈Γ是有限表示的,所以
是正合的.因此可以得到正合序列
即
正合.因此对任意有限生成左R-模N,可以得到图 2.
因为A和C是Ding f-投射左R-模,所以由引理1知,σN,A和σN,C是满的.由文献[5]的引理3.14知,σN,B也是满的.因此B是Ding f-投射模,故由所有Ding f-投射左R-模构成的类关于纯扩张封闭.
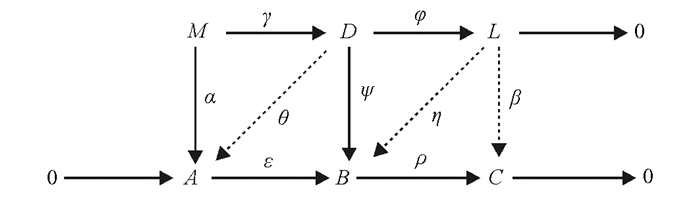
设R是左凝聚环,且$0 \to A\mathop \to \limits^\varepsilon B\mathop \to \limits^\rho C \to 0$是左R-模的纯正合序列.假设B是Ding f-投射左R-模.对任意有限生成左R-模M和任意同态α:M→A.因为B是Ding f-投射模,所以存在有限生成Ding投射左R-模D,γ:M→D和ψ:D→B,使得εα=ψγ.设$M\mathop \to \limits^\gamma D\mathop \to \limits^\varphi L \to 0$是正合序列.则存在β:L→C,使得图 3交换.
因为R是左凝聚环,所以D是有限表示的,且L也是有限表示的.又因为
是正合的.所以存在η:L→B,使得β=ρη.于是存在同态θ:D→A,使得α=θγ.因此A是Ding f-投射模. 故由所有Ding f-投射左R-模构成的类关于纯子模封闭.
由文献[11]知,如果每个有限生成无挠右R-模是有限表示的,则R是右Π-凝聚环.由文献[5]知,如果δM:M→M**是单同态,则左R-模M是无挠模.本文中,我们用DpdRM表示左R-模M的Ding投射维数.若存在最小的非负整数n,使得M有长度为n的Ding投射分解,则记DpdRM≤n;若n不存在,则记DpdRM=∞.我们用LDPD(R)表示R的左整体Ding投射维数,即
定理2 设R是右Π-凝聚环,且LDPD(R)≤n.若存在正合序列
其中Fi是f-投射模,则M是Ding f-投射模左R-模.
证 设
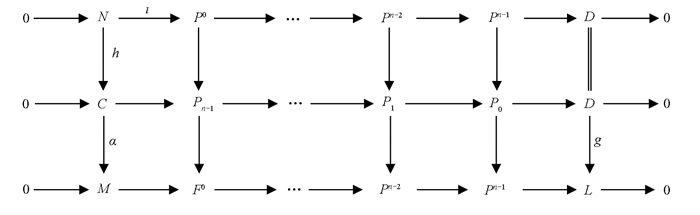
是正合序列.对任意有限生成左R-模N和同态f:N M,由文献[12]的推论3.12知,每个有限生成左R-模有f-投射预包络.因此,我们可以构造复形
其中每个Pi是有限生成投射的,使得对任意f-投射左R-模Q,上述序列是HomR(-,Q)正合的.因为D是有限表示的,所以存在正合序列
其中Pi是有限生成投射的.则C是有限生成Ding投射左R-模.我们可以得到图 4.
我们也可以得到图 5.
由同伦引理知,f-αh可以通过ι:N→P0分解.即存在β:P0→M,使得f=αh+βι.因此f可以通过有限生成Ding投射模左R-模C⊕P0分解.故M是Ding f-投射模.
On Ding f-Projective Modules
-
摘要: 引入了Ding f-投射左R-模的概念.证明了:由所有Ding f-投射左R-模构成的类关于直和以及直和项封闭;若R是左凝聚环,则由所有Ding f-投射左R-模构成的类关于纯扩张以及纯子模封闭.
-
关键词:
- Ding f-投射模 /
- Ding投射模 /
- 凝聚环
Abstract: In the paper, the concept of Ding f-projective left R-modules has been introduced. It shows that the class of all Ding f-projective left R-modules is closed under direct sums and direct summands, the class of all Ding f-projective left-modules is closed under pure extensions and pure submodules when is left coherent.-
Key words:
- Ding f-projective module /
- Ding projective module /
- coherent .
-

-
[1] doi: http://cn.bing.com/academic/profile?id=635e4deea206ac54fbecbc4e31fb243e&encoded=0&v=paper_preview&mkt=zh-cn ENOCHS E E, JENDA O M G.Gorenstein Injective and Projective Modules[J].Mathematische Zeitschrift, 1995, 200(1):611-633. [2] doi: http://d.old.wanfangdata.com.cn/NSTLQK/10.1016-0021-8693(87)90024-X/ AZUMAYA G.Finite Splitness and Finite Projectivity[J].JAlgebra, 1987, 106(1):114-134. [3] doi: http://d.old.wanfangdata.com.cn/Periodical/sxnk-e201104006 DING N Q, LI Y L, MAO L X.Strongly Gorenstein Flat Modules[J].JAustMathSoc, 2009, 86(3):323-338. [4] GILLESPIE J.Model Structures on Modules Over Ding-Chen Rings[J].Homology, Homotopy and Appl, 2010, 12(1):61-73. doi: 10.4310/HHA.2010.v12.n1.a6 [5] ENOCHS E E, JENDA O M G.Relative Homological Algebra[M].Berlin, New York:De Gruyter, 2000. [6] doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1080/00927872.2017.1365880 MAO L X.Rings Satisfying Every Finitely Generated Module Has a Gorenstein Projective (pre)Envelope[J].CommAlgebra, 2018, 46(5):2010-2022. [7] 叶星美, 杨晓燕. n-强F-Gorenstein投射模[J].西南大学学报(自然科学版), 2015, 37(10):84-88. doi: http://d.old.wanfangdata.com.cn/Periodical/xnnydxxb201510014 [8] 陈文静, 杨晓燕.强和强泛Gorenstein FP-内射模[J].西南大学学报(自然科学版), 2014, 36(8):75-78. doi: http://www.cnki.com.cn/article/cjfdtotal-xnnd201408012.htm [9] 李倩倩, 杨晓燕. n-强Gorenstein AC-投射模[J].西南师范大学学报(自然科学版), 2018, 43(12):36-40. doi: http://xbgjxt.swu.edu.cn/jsuns/jscnuhhse/ch/reader/view_abstract.aspx?file_no=20181208&flag=1 [10] YANG G, LIU Z K, LIANG L.Ding Projective and Ding Injective Module[J].Algebra Colloq, 2013, 20(4):601-612. doi: 10.1142/S1005386713000576 [11] doi: http://d.old.wanfangdata.com.cn/NSTLQK/10.1016-0021-8693(90)90252-J/ CAMILLO V.Coherence for Polynomial Rings[J].JAlgebra, 1990, 132(1):72-76. [12] doi: http://link.springer.com/article/10.1007/BF02567857 DING N Q, CHEN J L.Relative Coherence and Preenvelopes[J].ManusMath, 1993, 81(1):243-262. -



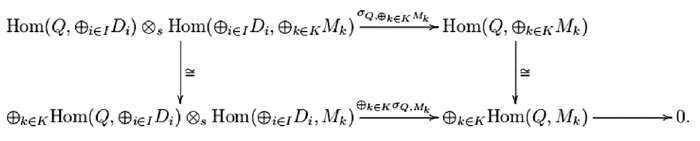
 下载:
下载: