-
戴维南等值方法通过简化电力系统, 提高了安全稳定评估的效率[1-8], 而戴维南等值参数的实时辨识是基于戴维南等值研究及应用的关键.现有的戴维南等值参数实时辨识方法通常就等值网络的负荷侧扰动状况进行研究[9-13], 而对于等值网络的系统侧扰动状况研究不多.
对于等值网络的扰动状况, 由于前后两个运行状况下的等值网络参数的变化, 那些基于两个运行状况或多个运行状况下的量测量进行戴维南等值参数实时辨识的方法存在辨识困难, 显然利用一个运行状况下的量测量进行戴维南等值参数的实时辨识可以满足等值网络系统扰动状况下的参数辨识要求.
现有的利用一个运行状况下的量测量进行戴维南等值参数实时辨识的方法主要是基于全微分的戴维南等值参数跟踪算法[14-18], 在等值网络等值参数初值确定的条件下, 该算法在原理上可以跟踪等值网络参数的变化, 但该算法对系统小扰动的适应能力不强, 等值网络参数的渐进变化将影响算法的辨识效果.
为改进对系统小扰动的适应能力, 文献[19]提出了一种小扰动状况下的戴维南等值参数辨识的方法, 该方法在系统和负荷扰动状况下都能跟踪辨识等值网络的戴维南等值参数.虽然文献[19]给出了戴维南等值参数辨识方法的基本原理, 但未就等值网络系统扰动状况下的戴维南等值参数辨识实现原理加以阐明, 为此本文就等值网络系统扰动状况下的戴维南等值参数辨识实现原理进行阐明, 最后通过仿真验证了辨识方法的准确性和有效性.
全文HTML
-
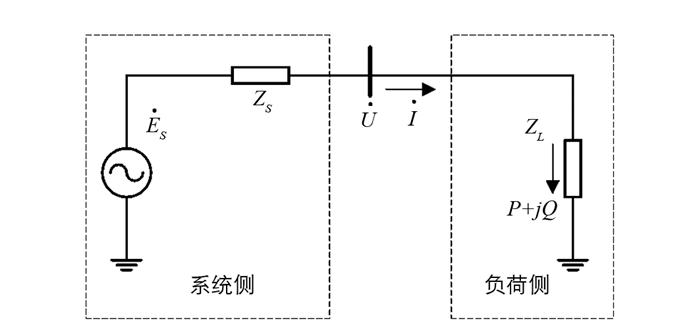
若从某一负荷向系统看进去, 任意k时刻的实际电力系统可以等值为一个含有电压源和阻抗部分, 与外部负荷构成图 1所示的简单两节点系统, 其数学模型可以描述为
其中,
$\dot E$ S和ZS分别为某等值系统在k时的戴维南等值电势和等值阻抗,$\dot U$ 为k时刻的负荷母线电压,$\dot I$ 为负荷电流, P、Q分别为负荷侧的有功功率、无功功率.等值母线处电压$\dot U$ 和电流$\dot I$ 与负荷ZL的关系如下 -
在等值母线处对左侧(系统侧)进行等值, 假定相邻时刻戴维南等值参数未发生太大变化, 则系统戴维南等值阻抗可由下式计算:
式中, 上标表示相邻时刻等值母线处电压电流的测量信息.
若扰动发生在系统侧, 负荷侧参数保持不变, 假定系统侧等值阻抗ZS变为ZS+ΔZS, 等值电势
$\dot E$ S保持不变, 将式(2)带入式(3)则有由上式可知, 若扰动仅存在于系统侧, 则辨识得到的等值参数为负荷侧的等值阻抗.因此, 等值系统的系统侧发生扰动, 传统戴维南等值方法无法准确跟踪等值参数的变化.
文献[19]的小扰动状况下的戴维南等值参数辨识方法利用暂态电量信号(当前运行状况下的量测量与前一运行状况下的量测量的差值)对等值网络参数进行辨识, 对于等值网络系统侧扰动而言, 由于扰动发生前后网络的参数不一致, 导致未知参数的个数增加, 无法对等值参数进行有效的辨识.等值网络系统侧扰动后的参数不变, 利用扰动后暂态过程中的量测量可有效辨识当前运行状况下的等值网络参数.
1.1. 戴维南等值方法的数学描述
1.2. 系统侧扰动下的戴维南等值分析
-
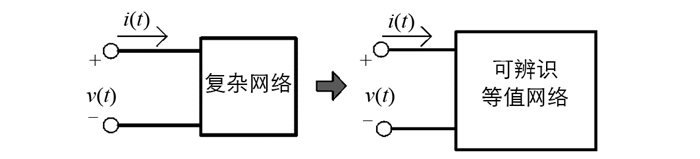
利用扰动后的量测信息辨识网络参数, 从而得到当前运行状况下结构和参数唯一确定的等值网络, 电力系统等值过程如图 2所示.
根据电路理论, 等值网络的电压电流约束关系可用K阶微分方程表示:
式中, v(t)和i(t)分别表示等值网络端口的电压和电流信号, v(t)(k)和i(t)(k)分别表示电压和电流信号的k阶微分求导, vs(t)表示等值网络的等效电源, vs(t)(k)表示等效电源的k阶微分求导, 微分方程的阶次K和系数ak、bk、ck(k=0, …, K)决定了等值网络的特性.
在系统实际运行中, 等值网络系统侧发生扰动的情况较为普遍, 等值网络系统侧扰动变化, 其参数会随之改变, 导致高阶微分方程中各系数改变, 其表征的网络特性也随之发生改变.等值网络系统侧发生扰动后的结构和参数保持不变, 对应当前运行状况下的等值参数, 高阶微分方程表征的等值网络的特性不变, 因而可利用扰动后的暂态过程中的电量信息辨识等值网络参数.
扰动后网络端口的电压电流信号为周期分量和暂态分量的叠加, 即
式中, iT(t)、vT(t)分别表示端口暂态电压、电流信号的周期分量, iNT(t)、vNT(t)表示相应暂态信号的暂态分量, vsT(t)表示暂态过程中的等效电源.
通过提取网络端口电压电流的暂态分量信号, 利用电压电流的暂态分量信号辨识等值网络当前运行状况下的等值参数.将式(6)带入式(5)中得到
取暂态过程中电压电流的相邻半个周期的信号, 可得:
由式(7)和式(8)可得:
式中,
$\mathit{\Delta }{v_{NT}}(t) = {v_{NT}}\left( {t + \frac{T}{2}} \right) + {v_{NT}}(t), \mathit{\Delta }{i_{NT}}(t) = {i_{NT}}\left( {t + \frac{T}{2}} \right) + {i_{NT}}(t)$ 分别表示电压和电流暂态分量信号.式(9)表示的高阶微分方程能够有效表征等值网络的特性.根据网络的实际特性建立相应的等值网络模型, 利用端口提取的暂态过程中的电压电流以及扰动后的稳态信号求解高阶微分方程系数ak和bk, 通过建立高阶微分方程系数与等值模型参数之间的关系, 即可求出等值模型的参数.
利用暂态分量信号辨识等值参数, 具体方法如下:令ΔvNT=Vmsin(ωt+φv), ΔiNT=Imsin(ωt+φi), 带入微分方程(9)中.
当K为偶数时, 令N=K/2, 并计算
当K为奇数时, 令N=(K-1)/2, 并计算
由此可得:
上式中左边部分提取
$\sqrt {A_0^2 + A_1^2} $ , 并令$\sin \theta = \frac{{{A_1}}}{{\sqrt {A_0^2 + A_1^2} }}, \cos \theta = \frac{{{A_0}}}{{\sqrt {A_0^2 + A_1^2} }}$ , 推导可得:对上式坐标进行平移变换, 可得
将上式进一步整理可得:
将上式改写为
$\mathit{\Delta }v = {R_{eq}}\mathit{\Delta }i + {L_{eq}}\frac{{{\rm{d}}\mathit{\Delta }i}}{{{\rm{d}}t}}$ 的形式, 得即可得到等值网络的等值电阻和等值电抗为
利用端口提取的暂态分量信号进行戴维南参数辨识, 能实时跟踪等值网络的参数变化, 得到的结果能进一步用于电力系统计算和分析, 使该等值系统更贴近于并反映系统的实际运行状况.
-
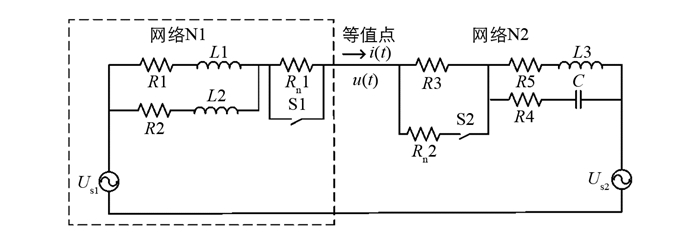
为了说明本文方法正确可行, 通过建立简单电路网络模型进行验证, 电路网络模型如图 3所示.
在图 3所示的简单电路网络中, Us1=220 V, Us2=35 V, 各支路阻抗参数如表 1所示, 将电路网络分为等值网络N1和外部网络N2.利用理想断路器S1和S2动作分别模拟等值网络N1的扰动和外部网络N2的扰动, 由此产生小扰动信号.仿真时间为0.2 s, 在t=0.1 s时理想断路器断开线路, 记录检测点电压电流信号, 采样频率设置为10 kHz. S1断开、闭合状态下网络N1的等值电阻电感真实值分别为:25 Ω, 0.5 H及20 Ω, 0.5 H. S2断开、闭合状态下网络N2的等值电阻电感真实值分别为:41.724 4 Ω、0.238 4 H及36.724 4 Ω, 0.238 4 H.
保持等值网络N1的断路器S1处于断开状态, 断开或闭合外部网络N2的S2, 模拟等值系统外部网络的扰动, 利用扰动状况下的暂态信号辨识戴维南等值参数, 结果如表 2所示.类似地, 保持负荷侧网络的断路器S2处于断开状态, 断开或闭合等值网络系统侧的S1, 模拟等值系统系统侧网络的扰动, 辨识的戴维南等值参数如表 3所示.
-
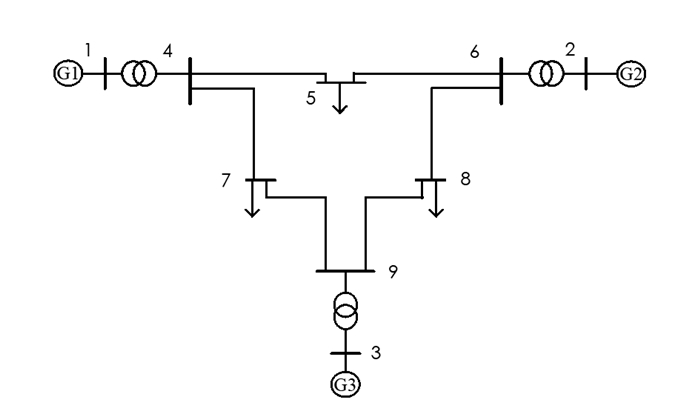
如图 4所示, 在IEEE9节点系统进行戴维南等值, 负荷设置如下:Bus5所接负荷为恒阻抗负荷和感应电动机的组合, Bus7和Bus8处的负荷大小不变、功率因数恒定, 通过调整Bus5负荷变化、系统结构变化进行辨识来验证本方法的准确性.
针对图 4所示的系统, 分别施以如下的扰动进行戴维南等值参数辨识:
1) 外部负荷变化:对Bus5处负荷减小1%作为外部扰动;
2) 等值系统网络结构变化:改变Bus4与Bus5间线路L45的长度作为等值系统扰动.
以上情况的仿真时间均为1.8 s, 扰动开始时刻均为1.5 s, 在Bus5处测量电压电流信号, 采样频率为10 kHz, 利用扰动下的三相电压电流暂态信号分别辨识戴维南等值参数, 辨识结果如表 4、表 5所示.
从表 4、表 5的戴维南等值参数辨识结果可知, 扰动后的A、B、C三相暂态电流电压信号辨识的等值参数非常接近, 说明利用扰动后暂态分量能够有效辨识戴维南等值参数.针对等值系统网络结构变化引起的等值参数变化, 该方法能够利用一个运行状态下的量测数据实时辨识等值系统的戴维南参数.
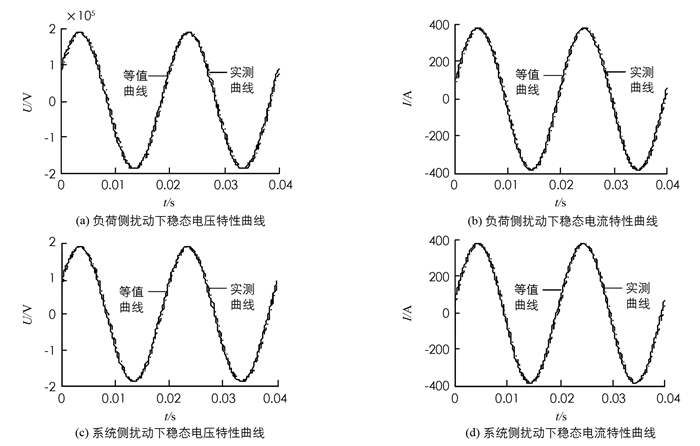
为了验证戴维南等值参数辨识结果的准确性, 对比稳态下Bus5处原系统实测曲线与等值系统仿真曲线.限于篇幅, 仅给出A相的电压电流, 如图 5所示, 其中, (a)和(b)为等值系统负荷变化时的电压电流稳态响应曲线, (c)和(d)为等值网络系统侧网络结构变化时的电压电流稳态响应曲线.
从以上仿真结果可以看出, 在等值系统负荷或网络结构变化时, 稳态响应曲线与实测曲线差别很小, 参数辨识的结果接近真值, 说明本文采用的戴维南等值参数辨识方法在等值系统内外扰动下均能准确辨识系统参数, 有效地解决了等值系统结构和参数变化的辨识问题.
3.1. 简单电路网络模型仿真
3.2. IEEE9节点系统仿真
-
本文提出了一种基于扰动后暂态分量信号的戴维南等值参数辨识方法, 通过建立能够表征等值网络实际特性的电路网络模型, 利用扰动后暂态电压电流信号求解出与之匹配的高阶微分方程系数, 然后等值网络稳态时参数与微分方程系数相关联, 从而求出等值系统的实时参数.简单电路网络和IEEE9节点系统的仿真结果表明, 利用端口提取的暂态分量信号能够跟踪等值网络的实时变化, 有效解决了等值网络扰动下等值参数的准确跟踪问题.



 下载:
下载: