在进一步讨论之前，给出如下引理.

引理1^[6]  设0 < α < 1，函数x(t)是分数阶微分方程

的解的充分必要条件是x(t)为如下Volterra积分方程的解

其中^CD_0，t^αx(t)表示Caputo意义下x(t)的α阶分数阶导数.

引理2^[6]  设0 < α < 1，函数x(t)是分数阶微分方程

的解的充分必要条件是x(t)为如下Volterra积分方程的解

其中^RLD_0，t^αx(t)表示Riemann-Liouville意义下x(t)的α阶分数阶导数.

引理3^[6]  设0 < α < 1，则

引理4   设0 < α < 1，φ(t)为区间[0，+∞)上的可微函数，若存在t₀>0使得φ(t₀)=0，且对t∈[0，t₀)有φ(t)≥0，则有

证  由$^{RL}D_{0, t}^\alpha \varphi (t) = \frac{1}{{\Gamma (1 - \alpha)}}\frac{{\rm{d}}}{{{\rm{d}}t}}\int_0^t {{{(t - \tau)}^{ - \alpha }}} \varphi (\tau){\rm{d}}\tau $，定义$H(t) = \int_0^t {{{(t - \tau)}^{ - \alpha }}} \varphi (\tau){\rm{d}}\tau $，则对任意h∈(0，t₀)，

由假设，对τ∈(0，t₀－h)⊂(0，t₀)有φ(τ)≥0且显然(t₀－τ)^－α－(t₀－τ－h)^－α < 0，故有I₁≤0. 从而

由文献[23]的结论可知

其中ξ∈(t₀－h，t₀)，η=t₀－ξ. 由假设φ(t)可微，有

若φ′(t₀)=0，则φ(t₀－h)=o(h)(h→0⁺)且$\mathop {\lim }\limits_{h \to {0^ + }} {\eta ^{ - a}}\varphi \left({{t_0} - \eta } \right) = 0$. 若φ′(t₀) < 0，则φ(t₀－h)~－φ′(t₀)h(h→0⁺)且$\mathop {\lim }\limits_{h \to {0^ + }} {\eta ^{ - a}}\varphi \left({{t_0} - \eta } \right) = 0$，从而可得

利用引理3与引理4，可直接得到如下结论.

引理5   设0 < α < 1，φ(t)为区间[0，+∞)上的可微函数，若存在t₀>0使得φ(t₀)=0且对t∈[0，t₀)有φ(t)≥0，则有^CD_0，t^αφ(t₀)≤0.

令分数阶导数的阶数α∈(0，1). 在本文定理1数量值函数f(t，x)与F(t，x)连续且对x满足Lipschitz条件、满足(9) 式且(7) 与(8) 式解函数存在的条件下，文献[22]将经典的整数阶导数意义下微分方程的比较定理推广到Caputo分数阶导数意义下微分方程的比较定理. 但在其定理证明过程中，对不同的解函数利用了(9) 式. 关键性条件的使用存在缺陷，定理的证明晦涩不易理解. 为解决其证明中存在的问题，下面对定理条件做了调整，不再要求数量值函数f(t，x)与F(t，x)对x满足Lipschitz条件，在数量值函数f(t，x)与F(t，x)连续、满足(9) 式以及解函数可微条件下重新给出比较定理，并利用上一部分的引理给出了较易理解的证明，并在定理1的基础上作了进一步的讨论、推广.

定理1  设f(t，x(t))，F(t，x(t))∈C([0，+∞)×$\mathbb{R} $，$\mathbb{R} $)且[0，+∞)上的可微函数x(t)，X(t)分别为如下分数阶微分方程的解

若对任意的(t，u)∈[0，+∞)×$\mathbb{R} $有

则对任意的t∈(0，+∞)有x(t) < X(t).

证  利用假设X(0)=x(0) 与(9) 式，有

故存在某正数δ>0，使得当0 < t < δ时，有F(t，X(t))－f(t，x(t))>0. 利用引理1，有

令φ(t)=X(t)－x(t)，则有

由于解函数x(t)，X(t) 连续，因此函数φ(t)在区间[0，t)连续. 假设t=t₀是第一个满足φ(t)=0的点，即当t∈(0，t₀)时φ(t)>0且φ(t₀)=0. 则利用条件(7)，(8) 与(9) 式，可以得到

另一方面，由φ(0) =X(0) －x(0) =0以及引理3-5可知

这与(10) 式矛盾，故这样的t₀点不存在，所以对任意的t∈(0，+∞)总有x(t) < X(t).

直接利用定理1，可以得到如下推论.

推论1   设h(x(t))∈C([0，+∞)×$\mathbb{R} $，$\mathbb{R} $)，f(t)，F(t)∈C([0，+∞)，$\mathbb{R} $)且[0，+∞)上的可微函数x(t)，X(t)分别为如下两个方程的解

若对任意的t∈[0，+∞)有f(t) < F(t)，则对任意的t∈(0，+∞)有x(t) < X(t).

当定理1中条件(9) 式的不等号非严格时，有如下结论.

定理2   设f(t，x(t))，F(t，x(t))∈C([0，+∞)×$\mathbb{R} $，$\mathbb{R} $)，且[0，+∞)上的可微函数x(t)，X(t)分别是方程(7) 与(8) 的解. 若对任意取定的t，函数f(t，u)或F(t，u)关于u单调不减且满足

则有x(t) < X(t)，t∈(0，+∞).

证  令$\varepsilon = \frac{1}{2}\left| {F\left({0, {x_0}} \right) - f\left({0, {x_0}} \right)} \right|$，则由f(0，x₀) < F(0，x₀)可知ε>0. 因此存在正数δ>0，使得

当0 < t < δ时，由定理1可知x(t) < X(t). 设t₁是区间[δ，+∞)内第一个使得不等式x(t) < X(t)不成立的点，故有

利用引理1可以得到

由于当τ∈(0，t₀)时(t₀－τ)^α－1>0，因此至少存在一点ξ₁∈(0，t₀)使得

利用引理1类似可得

由τ∈(0，t₁)时(t₁－τ)^α－1>0及(16) 式，存在一点ξ₂∈(0，t₁)使得

由(15) 式，有x(ξ₂) < X(ξ₂). 不妨设取定参数t时函数f(t，u)关于u单调不减，则有

结合(17) 式便有f(ξ₂，X(ξ₂))>F(ξ₂，X(ξ₂)). 这与假设中的条件f(t，u)≤F(t，u)矛盾. 因此当t∈(0，+∞)时有x(t) < X(t).

推论2   设h(x(t))∈C([0，+∞)×$\mathbb{R} $，$\mathbb{R} $)，f(t)，F(t)∈C([0，+∞)，$\mathbb{R} $)且[0，+∞)上的可微函数x(t)，X(t)分别为方程(12) 与(13) 的解. 若f(0) < F(0) 且当t∈(0，+∞)时f(t)≤F(t)，h(u)关于u单调不减，则有x(t) < X(t)，t∈(0，+∞).

定理1与定理2中的结论，将整数阶导数意义下常微分方程的比较定理推广到了Caputo意义下分数阶微分方程的比较定理. 利用引理3，类似于上述结论可以得到Riemann-Liouville意义下分数阶微分方程的比较定理.

定理3   设f，F∈C([0，+∞)×$\mathbb{R} $，$\mathbb{R} $)且[0，+∞)上的可微函数x(t)，X(t)分别满足方程

若对任意的(t，x)∈[0，+∞)×$\mathbb{R} $有

则有x(t) < X(t)，t∈(0，+∞).

类似于定理2，可将定理3进行推广如下.

定理4  设f，F∈C([0，+∞)×$\mathbb{R} $，$\mathbb{R} $)且[0，+∞)上的可微函数x(t)，X(t)分别满足方程(19) 与(20). 若对任意取定的t，函数f(t，u)或F(t，u)关于u单调不减且满足

则有x(t) < X(t)，t∈(0，+∞).

推论3   设h(x(t))∈C([0，+∞)×$\mathbb{R} $，$\mathbb{R} $)，f(t)，F(t)∈C([0，+∞)，$\mathbb{R} $)且[0，+∞)上的可微函数x(t)，X(t)分别满足如下两个方程

若对任意的t∈[0，+∞)有f(t) < F(t) 或f(0) < F(0) 且当t∈(0，+∞)时f(t)≤F(t)，h(u)关于u单调不减，则有x(t) < X(t)，t∈(0，+∞).

利用定理1与定理3，考虑一类分数阶微分方程解的稳定性.

定理5  设t∈[0，+∞)，ax < f(t，x) < bx，其中a < 0，b < 0. 若[0，+∞)上的可微函数x(t)为如下方程的解

则方程(25) 的解x(t)是全局Mittag-Leffler渐近稳定的.

证  设x₁(t)与x₂(t)分别为如下两个方程的解

则由文献[24]知x₁(t)=x(0) E_p(at^p)，x₂(t)=x(0) E_p(bt^p)，其中E_p(at^p)与E_p(bt^p)为Mittag-Leffler函数.

由定理1可知x₁(t) < x(t) < x₂(t). 根据Mittag-Leffler函数的渐近性质^[4]，有$\mathop {\lim }\limits_{t \to + \infty } {E_p}\left({b{t^p}} \right) = \mathop {\lim }\limits_{t \to + \infty } {E_p}\left({a{t^p}} \right) = 0$. 所以方程(25) 的解x(t)是全局Mittag-Leffler渐近稳定的.

类似可得如下结论：

定理6  设t∈[0，+∞)，ax < f(t，x) < bx，其中a < 0，b < 0. 若[0，+∞)上的可微函数x(t)为如下方程的解

则方程(26) 的解x(t)是全局Mittag-Leffler渐近稳定的.

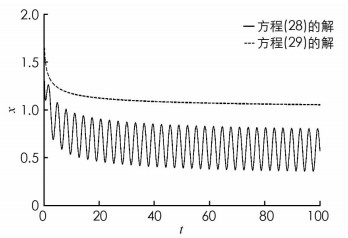
例1  考虑分数阶松弛-振动方程

其中：0 < α≤2，A为松弛系数，x(t)为应力，f(t)为弹性模量与应变率的乘积或者是外部激励. 为保持整数阶松弛-振动方程对初值的要求，方程中采用的是Caputo分数阶导数定义. 此方程为分数阶松弛-振动现象的控制方程^[25-26]. 当0 < α < 1时，方程表现为记忆性的慢速耗散现象，是分数阶松弛方程；当1 < α < 2时，方程表现为阻尼振动，是分数阶振动方程；α=1，2时方程分别表示整数阶的松弛方程和振动方程. 考虑松弛方程

记x(t)与X(t)分别表示方程(28) 与(29) 的解. 显然f(t，x(t)) < F(t，x(t))，故由定理1可得x(t) < X(t). 利用文献[11]中的方法可得方程(28) 与(29) 的数值解曲线，如图 1所示. 图 1的结果显示系统(28) 的应力x(t)从初值x(0) =2开始衰减并呈现出周期震荡. 系统(29) 的应力X(t)从初值X(0) =2开始呈现出应力松弛，且应力X(t)的曲线始终在应力x(t)的曲线上方. 这与理论结果相吻合.

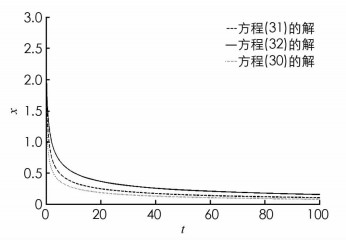
例2  考虑如下3个方程

由文献[22]，方程(30) 与(32) 具有解析解且全局Mittag-Leffler渐近稳定，方程(31) 难以得出其解析解. 但显然当x>0时－2x < －x－0.5|sin(x)| < －x，当x < 0时－2x>－x－0.5|sin(x)|>－x，故由定理5可知方程(31) 的解曲线是全局Mittag-Leffler渐近稳定的. 方程(30) -(31) 的数值解曲线如图 2所示. 图 2中，点线、虚线、实线分别表示方程(30)，(31) 与(32) 的解曲线，图中解曲线相对位置与变化趋势与理论结果相符.

本文基于函数在某点处分数阶导数符号的判定以及分数阶微分方程与Volterra积分方程的等价性，得到了一类分数阶微分方程的比较定理. 定理的结果表明，对于Caputo导数(或Riemann-Liouville导数)意义下的微分方程来说，不同的方程在满足一定条件时，相应方程的解曲线之间是不相交的.