MapReduce是一个编程范例，用于在分布式环境中处理大数据集，MapReduce框架为大数据提供了一个可扩展的容错环境. 在MapReduce范例中，Map阶段执行过滤和排序，Reduce阶段执行分组和聚合操作.

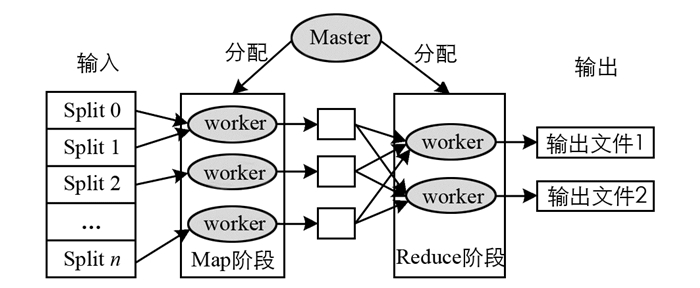
图 1给出了MapReduce框架流程. 一个节点被选为负责分配工作的Master，其余的都是Worker，输入数据分为多个Split，Master设备分配给Map Worker. 每个Worker处理相应的输入Split，生成<键/值>对并将其写入中间文件(在磁盘或内存中). Master通知Reduce阶段Worker关于中间文件的位置和读取数据，根据Reduce阶段处理它. 最后，将数据写入输出文件.

MapReduce范例的主要贡献是可扩展性，因为MapReduce允许在大量节点上进行高度并行化和分布式执行任务. 在MapReduce范例中，Map或Reduce任务分成多个作业，这些作业被分配给网络中的节点，通过将任何失败节点的作业重新分配到另一个节点来实现可靠性. 开源MapReduce在Hadoop分布式文件系统(HDFS)之上实现.

Hadoop MapReduce的主要优点之一是允许非专家用户轻松地对大数据运行分析任务. Hadoop MapReduce使用户可以完全控制输入数据集的处理方式，用户使用Java编写查询代码，便于多数没有数据库背景，只需具备Java基础知识的开发人员使用.

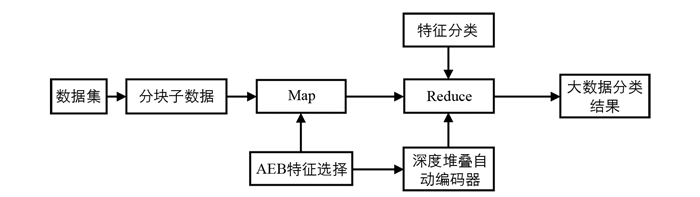
本文基于自适应指数蝙蝠和SAE的并行大数据分类方法，Map阶段使用AEB算法从数据库中选择特征. 然后，将选定的特征提供给Reduce进行大数据分类，Reduce阶段使用深度堆叠自动编码器进行大数据分类，该编码器由AEB算法选择特征训练而成. 图 2给出了基于AEB堆叠自动编码器算法进行大数据分类的框图.

将输入的大数据集合视为H，并将多个属性表示为H=x_nm，1≤m≤G，1≤n≤q. 其中，x_nm表示第m个数据的第n个属性的大数据，所有数据均由G个数据点和q个属性组成.

特征提取是Map阶段的重要功能，其中选择相关特征通过减小维度来最大程度地提高分类精度. Map阶段使用AEB算法选择特征.

AEB算法是将指数加权移动平均值(Exponential Weighted Moving Average，EWMA)和自适应权重策略引入到蝙蝠算法中得到的.蝙蝠算法作为一种著名的启发式算法，模拟了蝙蝠回声定位的行为，具有模型简单，收敛速度快，分布均匀等特点. 对于第a个蝙蝠在第h+1次迭代中的蝙蝠速度v_a^h+1和位置A_a^h+1，表示为：

其中，A_a^h+1表示第a个蝙蝠在第h+1次迭代中的位置，A_a^h表示第a个蝙蝠在第h次迭代中的位置，A_bat^*表示蝙蝠的最佳位置，v_a^h表示蝙蝠在第h次迭代中的速度，f_α表示第a个蝙蝠的频率，f_α=f_min+(f_max－f_min)×ω，ω∈[0, 1]是遵循正态分布的随机数. 蝙蝠算法的位置更新公式为：

ε∈[-1, 1]是一个随机数，L_mean^h表示第h次迭代中所有响度的平均值. 随着蝙蝠接近其目标，响度L和发射速率r，如以下公式进行更新.

其中，r_a⁰为初始发射速率，γ和ψ是一个常数，γ表示脉冲频数增加系数，γ>0，ψ表示脉冲响度减弱系数，0 < ψ < 1. 将式(1)中两个式子融合得到蝙蝠算法表达式为：

指数加权移动平均值(EWMA)是平均数据的过程，以获得较少的权重随时间而被删除的数据，可表示为：

A_EWMA^h和A_EWMA^h－1表示当前和上一次迭代的记录，β为常数，取值范围为0到1. 当前的预测取决于历史值乘权重，变化的采样间隔会迅速生成有关过程的信息，可以防止连续产生不良结果. 指数蝙蝠算法是将EWMA融合进蝙蝠算法，可表示为：

AEB算法是通过引入自适应速度的概念而得到的，蝙蝠个体继承上一代的速度，并获得最佳个体飞行，当算法进行到后期时，大多数蝙蝠个体都会陷入局部优化，而蝙蝠的速度无法使其逃脱局部优化，为了解决这个问题，本文提出了自适应蝙蝠速度算法. 该算法基于每个蝙蝠的适应度(距离越近适应的最佳距离值越高，距离越远值越低)，给其速度加上权重，如果个体比其他个体更接近最优解，则其适应价值更高，此时迅速放慢个体速度，使个体收敛到最优解，在这种情况下给出较小的权重值. 相反，如果个体的适应价值非常低，则意味着个体距离最佳解决方案还很远，需要给它更大的权重值. 权重计算方法设计为：

e_a^score_ah定义为：

大数据被分为数据子集，表示为x_nm={q_e}，1≤e≤F，数据子集的总数等于Map阶段中的映射器数量，表示为D={D1，…，DF}，其中F是从大数据开发的总子集数. Map的输入由E个总属性组成，表示为：

其中，M < G表示第e个子集的总数据点. 本文所提出的AEB算法在Map阶段用于选择最佳特征. 将数据输入到Reduce阶段，使用AEB算法处理生成最优特征. 为了提供更好的性能，选择具有最大值的适应度输出作为最佳解. AEB特征选择被描述为：

其中，选择特征的总数表示为l. 解向量是特征尺寸为[1×l]的向量.

在MapReduce处理框架中，首先对大数据集进行不同子集的划分，每个子集对应不同的Split，然后在Map进行特征选择，输出键值对为<分类准确率，特征>，对所有分类准确率进行排序，选择最大的分类准确率，其对应的特征即为最终特征，所有特征以集合形式输入Reduce阶段.

在Map阶段将获得的AEB算法用于从数据库中选择特征. 并且在Reduce阶段使用的深度堆叠自动编码器由AEB训练而成.

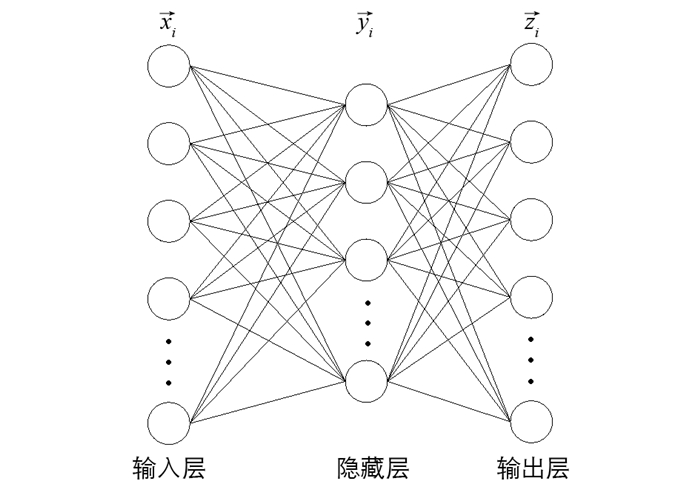
使用最常用的深度学习方法深度堆叠自动编码器对Map中选定的特征进行分类，深度堆叠自动编码器是一个对称的神经网络，用于无人监督方式学习数据集的特征，分为3层：输入层、隐藏层和输出层. 输入层完全连接到隐藏层，隐藏层进一步连接到输出层，如图 3所示.

给定一组训练样本$\{ {{\vec x}_1}, {{\vec x}_2}, {{\vec x}_3}, \cdots \} $，其中${{\vec x}_i} \in {R^n}$，n表示输入层的大小. 堆叠自动编码器首先通过应用线性映射和非线性激活函数f(x)将输入向量${{\vec x}_i} $编码为隐藏表示${{\vec y}_i} $，其中${{\vec y}_i} \in {R^m} $，m表示隐藏层的大小. 然后，通过应用线性映射和非线性激活函数g(x)将${{\vec y}_i} $解码重建为${{\vec z}_i} $，这两个步骤可由式(11)和式(12)表示为：

其中，W₁是编码权向量，b₁是编码偏置向量，W₂是解码权向量，b₂是解码偏置向量. f(·)和g(·)表示非线性的输入和输出映射函数，采用Sigmoid函数可表示为f(x)=1/[1+exp(－x)]. 深度自动编码器为了使隐藏层稀疏，使用稀疏约束最小化重构误差，这种架构被称为稀疏自编码器.

其中，α表示惩罚系数，ρ表示稀疏参数(通常是一个非常小的值，接近零). ${{\hat \rho }_j} = \sum\nolimits_{i = 1}^N {{{\vec y}_i}\left[ j \right]/N} $表示第N个训练样本上第j个隐藏单元的平均激活度.${KL(\rho \left\| {{{\hat \rho }_j})} \right.} $表示Kullback-Leibler (KL)散度，KL是用来测量两个不同分布之间差异的标准函数，可表示为：

其中，ρ被设置为接近0的值.$KL(\rho \left\| {{{\hat \rho }_j})} \right. $随着ρ和${{{\hat \rho }_j}} $之间的差减小而单调减小，如果$\rho = {{\hat \rho }_j} $，则$KL(\rho \left\| {{{\hat \rho }_j})} \right. = 0 $.

多层自动编码器是多个自动编码器的串联，是将连续层输入与堆叠在该层上的自动编码器输出连接的过程. 对于第p层，激活输出为：

式(15)中，g_p－1，m^G为p-1层的输出，M_p-1表示p-1层的权重，d_p－1^G表示p-1层的偏置. 式(16)中，K表示神经网络层数. C_M，A(·)表示多层稀疏自动编码器函数，g_1，m=q_m. 考虑到C_M，A(q_m^G)=g_ap，m^G，成本函数可以表示为：

深层自动编码器包含3个过程. ①初始化成本函数局部最小值附近的各个自动编码器参数. ②学习到下一个自动编码器隐藏层的输入. ③执行反向传播进行微调，通过同时更改所有模型参数，可以改善整体分类性能.

将本文所提AEB堆叠自动编码器的大数据分类方法进行实验，并通过现有方法对本文方法进行比较分析，以证明本文方法的有效性. 本文所有实验在Windows 10操作系统的电脑中运行. MapReduce实验环境由6台集群结点组成，选取1台作为主节点，另外5台作为从节点，每个节点的配置如下：Intel Core i5-8GB，RAM为64 G，硬盘容量为1 T，软件配置为CentOS 6.5，Hadoop版本为5.4.5，6个节点都连接在100 Mb的交换机上.

本文采用准确度(Accuracy)和真正例率(TPR)这两个指标评估模型的性能，数学定义为：

当一个样本为正类，且被预测为正类时，称为真正类(TP)；假若负类被预测为正类，称为假正类(FP)；假若是负类被预测成负类，称为真负类(TN)；假若正类被预测为负类，称为假负类(FN).

本文使用的两个标准数据集分别是加州大学欧文分校(UCI)机器存储库中Cleveland数据集和Pima India数据集. 对比算法有：文献[11]中的KNN大数据分类方法，文献[13]中SVM分类方法，文献[14]中蚁群优化-人工神经网络联合算法以及文献[15]中蝙蝠算法+人工神经网络. 对比实验通过改变组合数据集中训练数据的百分比来对不同方法进行分析. 经过多次实验，本文对于自适应蝙蝠算法的参数设置为：种群200，迭代次数70，初始发射速率0.95，响度衰减系数0.95，频度增加系数0.5.

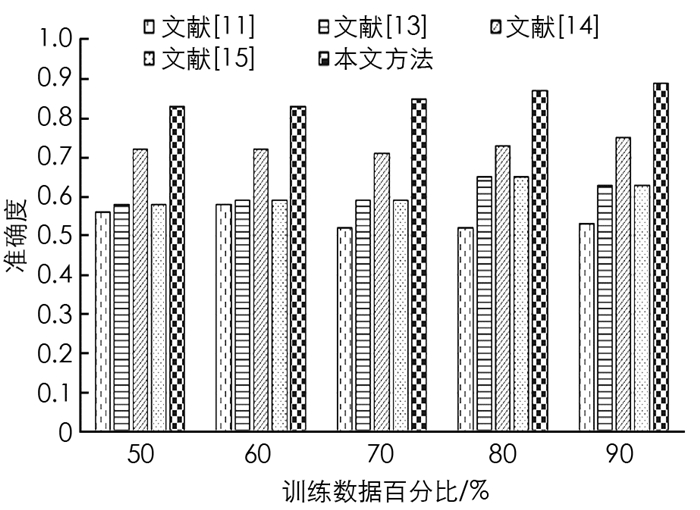
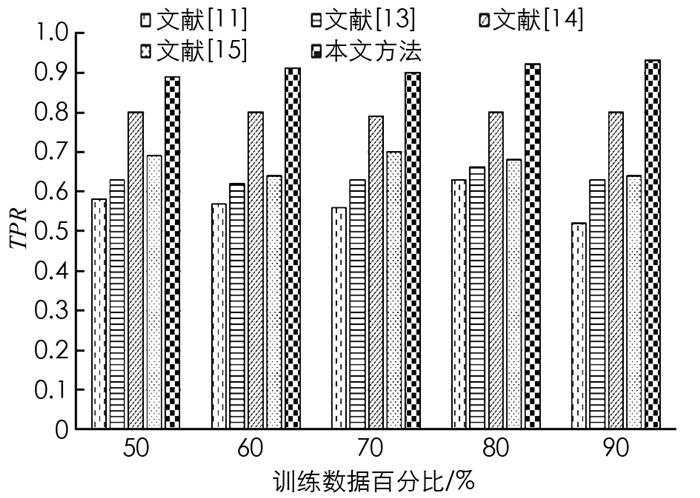
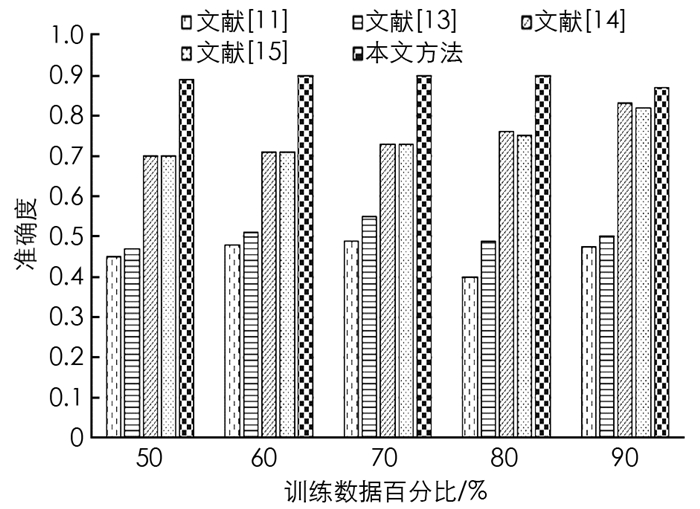
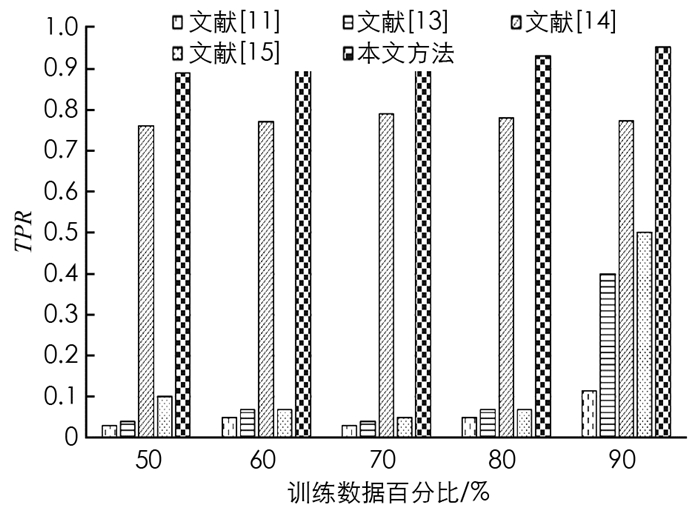
图 4和图 5给出了Cleveland数据集中不同训练数据在百分比条件下准确度和TPR的对比结果.

从图 4和图 5中的对比数据可以看出，在Cleveland数据集上针对不同训练数据百分比，本文所提算法的准确度都优于其他4种方法. 在训练数据百分比为90%时，本文所提算法具有最高的准确度，达到0.887 5，这是因为本文所提算法设计了自适应指数蝙蝠算法来选择最优特征，增加了分类准确度，同时深度堆叠自动编码器通过AEB训练得到的分类结果更加准确. 文献[14]中蚁群优化-人工神经网络联合算法准确度次之，这是因为使用了深度人工神经网络，并进行了蚁群优化，提升了分类准确度. 文献[15]中蝙蝠算法+人工神经网络算法使用了蝙蝠算法优化人工神经网络，但是由于蝙蝠算法的局限性，导致其分类准确度与SVM分类性能接近. 在Cleveland数据集上，针对不同训练数据百分比，本文所提算法的TPR都优于其他4种方法，在训练数据百分比为90%时，本文所提算法具有最高的真正例率，达到0.928 9. 这是因为本文AEB+堆叠自动编码器对分类性能的提升.

图 6和图 7给出了Pima India数据集上不同训练数据在百分比条件下准确度和TPR的对比结果.

从图 6和图 7中数据可以看出，当训练数据百分比达到80%时，Pima India数据集上本文所提算法的准确度最高；当训练数据百分比达到90%时，TPR最高. 而且，在所有不同训练数据百分比条件下，本文所提算法的性能都比其他算法高，说明了本文方法的有效性.

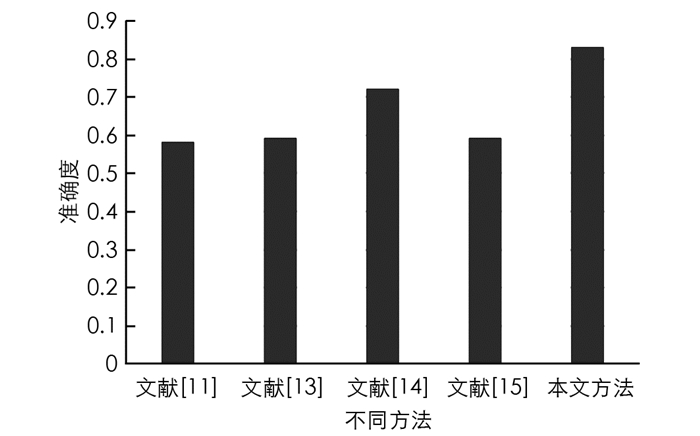
为了验证本文方法在大数据集上的优越性能，在Higgs大数据集上给出性能对比结果. Higgs大数据集样本数量为11 000 000，特征向量28，标签数量42.

从图 8中可以看出，本文方法在Higgs大数据集上的准确度能够达到0.83，比文献[14]算法准确度提高了0.11. 针对不同的大数据集，本文所提方法能够以高精度实现大数据分类，且分类性能优于其他方法，说明了本文方法的普适性和优越性.

针对大数据分类性能低的问题，本文提出一种自适应指数蝙蝠和SAE的并行大数据分类方法，该方法在Map阶段使用设计的自适应指数蝙蝠算法进行特征选择；在Reduce阶段使用经过AEB算法训练的深度堆叠自动编码器进行分类，进一步提升了分类性能. 使用不同的实验数据集对本文所提方法进行实验，不同百分比条件下的分类性能结果显示，本文所提方法能够以高精度实现大数据分类，且在准确度和TPR性能方面都优于现有其他方法，说明本文方法的有效性和优越性. 未来的工作将通过扩展本文所提出的方法来处理安全约束.