高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

有机材料中激子裂变过程的演化模型

,  , 

上一篇

下一篇

刘玲, 曾俊杰, 张勇. 有机材料中激子裂变过程的演化模型[J]. 西南师范大学学报(自然科学版), 2022, 47(10): 1-6. doi: 10.13718/j.cnki.xsxb.2022.10.001
引用本文: 刘玲, 曾俊杰, 张勇. 有机材料中激子裂变过程的演化模型[J]. 西南师范大学学报(自然科学版), 2022, 47(10): 1-6. doi: 10.13718/j.cnki.xsxb.2022.10.001
shu
LIU Ling, ZENG Junjie, ZHANG Yong. On Evolution Models of Exciton Fission in Organic Materials[J]. Journal of Southwest China Normal University(Natural Science Edition), 2022, 47(10): 1-6. doi: 10.13718/j.cnki.xsxb.2022.10.001
Citation: LIU Ling, ZENG Junjie, ZHANG Yong. On Evolution Models of Exciton Fission in Organic Materials[J]. Journal of Southwest China Normal University(Natural Science Edition), 2022, 47(10): 1-6. doi: 10.13718/j.cnki.xsxb.2022.10.001
shu

有机材料中激子裂变过程的演化模型

  • 西南大学 物理科学与技术学院/微纳结构光电子学重庆市重点实验室, 重庆 400715

  • 基金项目: 国家自然科学基金资助项目(61475126)
详细信息
    作者简介:

    刘玲, 硕士研究生, 主要从事有机发光材料与器件研究 .

    通讯作者: 张勇, 博士, 教授, 硕士研究生导师

  • 中图分类号: O571.43+1

On Evolution Models of Exciton Fission in Organic Materials

  • School of Physical Science and Technology, Southwest University/Chongqing Key Laboratory of Micro and Nano Structure Optoelectronics, Chongqing 400715, China

  • 摘要: 采用耦合的微分方程组对具有激子裂变特性的红荧烯材料的瞬态发光衰减过程进行理论拟合. 其中一组微分方程组来源于传统的两步三状态演化模型, 另一组则来源于新确立的三步四状态演化模型. 通过方程组的迭代运算可以反映材料中单重态激子裂变过程的动态变化. 拟合结果显示, 四状态模型对激子裂变过程的描述较之三状态模型更加合理, 拟合曲线与实验曲线符合度更好. 另外, 对曲线拟合所用的速率参数随温度的变化进行了指数拟合, 进而得到红荧烯材料激子裂变过程的能量差值. 拟合结果同样显示, 相较于三状态模型, 四状态模型拟合得到的能量差更接近准确值.
    Abstract: The coupled differential equations have been utilized to fit the transient fluorescence decay from rubrene material, which had the property of singlet exciton fission. One set of coupled differential equations was derived from a traditional two-step/three-state evolution model. Another set of coupled differential equations was derived from a newly established three-step/four-state evolution model. The dynamic change of singlet exciton fission process could be depicted by the iterative operations of the above two set of equations. The simulated results show that four-state model was more reasonable than three-state model for the description of singlet exciton fission. The simulating curves were more coincide with experimental curves. In addition, we adopted the exponential laws to fit the variation of rate constants at different temperatures. Furthermore, the energy difference of fission process in rubrene could be obtained. Similarly, the simulating results showed that the value of energy difference obtained by using four-state model was more accurate than that from three-state model.
  • 加载中

  • 图 1  红荧烯薄膜的光致发光谱

    下载: 全尺寸图片 幻灯片

    图 2  掺杂薄膜的瞬态发光衰减

    下载: 全尺寸图片 幻灯片

    图 3  不同温度下的瞬态发光衰减曲线及其拟合结果

    下载: 全尺寸图片 幻灯片

    图 4  速率k-2-1/T与k2-1/T的指数拟合图

    下载: 全尺寸图片 幻灯片
  • [1] SHOCKLEY W, QUEISSER H J. Detailed Balance Limit of Efficiency of P-n Junction Solar Cells [J]. Journal of Applied Physics, 1961, 32(3): 510-519. doi: 10.1063/1.1736034
    [2] PACI I, JOHNSON J C, CHEN X D, et al. Singlet Fission for Dye-Sensitized Solar Cells: Can a Suitable Sensitizer Be Found?[J]. Journal of the American Chemical Society, 2006, 128(51): 16546-16553. doi: 10.1021/ja063980h
    [3] HANNA M C, NOZIK A J. Solar Conversion Efficiency of Photovoltaic and Photoelectrolysis Cells with Carrier Multiplication Absorbers [J]. Journal of Applied Physics, 2006, 100(7): 074510-1-074510-8. doi: 10.1063/1.2356795
    [4] SMITH M B, MICHL J. Singlet Fission [J]. Chemical Reviews, 2010, 110(11): 6891-6936. doi: 10.1021/cr1002613
    [5] 杨小丽, 何丽红, 连亚军, 等. 基于长链胺及聚合物的高效蓝色发光器件[J]. 西南师范大学学报(自然科学版), 2021, 46(9): 43-49. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xsxb.2021.09.006
    [6] SCHOLES G D. Correlated Pair States Formed by Singlet Fission and Exciton-Exciton Annihilation [J]. The Journal of Physical Chemistry A, 2015, 119(51): 12699-12705. doi: 10.1021/acs.jpca.5b09725
    [7] PENSACK R D, OSTROUMOV E E, TILLEY A J, et al. Observation of Two Triplet-Pair Intermediates in Singlet Exciton Fission [J]. The Journal of Physical Chemistry Letters, 2016, 7(13): 2370-2375. doi: 10.1021/acs.jpclett.6b00947
    [8] BREEN I, TEMPELAAR R, BIZIMANA L A, et al. Triplet Separation Drives Singlet Fission after Femtosecond Correlated Triplet Pair Production in Rubrene [J]. Journal of the American Chemical Society, 2017, 139(34): 11745-11751. doi: 10.1021/jacs.7b02621
    [9] MA L, ZHANG K K, KLOC C, et al. Singlet Fission in Rubrene Single Crystal: Direct Observation by Femtosecond Pump-Probe Spectroscopy [J]. Physical Chemistry Chemical Physics: PCCP, 2012, 14(23): 8307-8312. doi: 10.1039/c2cp40449d
    [10] 田恪明, 吴健荣. 模糊拟度量在复杂性分析中的应用[J]. 西南大学学报(自然科学版), 2021, 43(10): 110-116. doi: https://www.cnki.com.cn/Article/CJFDTOTAL-XNND202110015.htm
    [11] PILAND G B, BURDETT J J, KURUNTHU D, et al. Magnetic Field Effects on Singlet Fission and Fluorescence Decay Dynamics in Amorphous Rubrene [J]. The Journal of Physical Chemistry C, 2013, 117(3): 1224-1236. doi: 10.1021/jp309286v
    [12] LI J, CHEN Z H, ZHANG Q M, et al. Temperature-Dependent Singlet Exciton Fission Observed in Amorphous Rubrene Films [J]. Organic Electronics, 2015, 26: 213-217. doi: 10.1016/j.orgel.2015.07.035
  • 加载中
图( 4)
计量
  • 文章访问数:  1496
  • HTML全文浏览数:  1496
  • PDF下载数:  239
  • 施引文献:  0
出版历程
  • 收稿日期:  2021-11-02
  • 刊出日期:  2022-10-20

有机材料中激子裂变过程的演化模型

    通讯作者: 张勇, 博士, 教授, 硕士研究生导师
    作者简介: 刘玲, 硕士研究生, 主要从事有机发光材料与器件研究
  • 西南大学 物理科学与技术学院/微纳结构光电子学重庆市重点实验室, 重庆 400715
  • 收稿日期:  2021-11-02
基金项目:  国家自然科学基金资助项目(61475126)

摘要: 采用耦合的微分方程组对具有激子裂变特性的红荧烯材料的瞬态发光衰减过程进行理论拟合. 其中一组微分方程组来源于传统的两步三状态演化模型, 另一组则来源于新确立的三步四状态演化模型. 通过方程组的迭代运算可以反映材料中单重态激子裂变过程的动态变化. 拟合结果显示, 四状态模型对激子裂变过程的描述较之三状态模型更加合理, 拟合曲线与实验曲线符合度更好. 另外, 对曲线拟合所用的速率参数随温度的变化进行了指数拟合, 进而得到红荧烯材料激子裂变过程的能量差值. 拟合结果同样显示, 相较于三状态模型, 四状态模型拟合得到的能量差更接近准确值.

English Abstract

    全文HTML

1.   理论模型

  • 在光伏器件中，通常材料吸收一个光子可激发一个激子，如果这个激子解离成自由载流子并被电极收集，则该器件的光电转化效率即为100%. 考虑到各种损耗，理论上可以估算出光伏器件能量转化效率的Shockley-Queisser极限约为34%[1]. Paci等[2]在2006年提出，可以利用单重态激子裂变(简称激子裂变)特性来进一步提高有机光伏器件的光电转化效率. 如果将具有激子裂变特性的材料作为新型敏化剂添加到器件的功能层中，理论估算有望将器件的光电转化效率提升至45%左右[3]，由此引发了国内外研究者对激子裂变材料和激子裂变过程的普遍关注. 激子裂变过程是一种在某些特殊有机材料中激子数倍增的现象，在这些材料中由光或电激发产生一个具有较高能态的单重态激子S1，而后S1态激子将其一半的能量转移给另一个处于基态的分子S0，因而S1态激子和S0态分子就快速转变为两个具有较低能态的三重态激子T1. 此前，激子裂变的演化过程通常用一个传统的两步三状态演化模型来描述[4]：

    其中：1(TT)i态是由两个T1态激子耦合形成的中间过渡态；k-2，k2，k-1，k1是不同状态间相互转化的速率. 由公式(1)可见，激子裂变过程是可逆的，其逆过程被称为三重态激子的聚变(简称激子聚变)，一般情况下这两种过程共存.

    Paci等[2]提出的策略利用了有机材料的两个特点：首先，材料吸收一个光子后可通过激子裂变过程产生两个T1态激子，从而实现激子数量的倍增；其次，有机材料中一般T1态激子比S1态激子的寿命更长[5]，这非常有利于激子扩散到界面附近进行拆分解离. 然而，有一些理论和实验研究表明[6-8]，当中间过渡态1(TT)i态向(T1+T1)态转变时，其转变过程并非如公式(1)那样简单直接. 与公式(1)不同的是，两个T1态激子最初经过空间上的分离令其空间波函数的交叠解除，但此时二者间仍然保持一定强度的自旋相互作用，形成另一个中间过渡态1(T…T)，而后再经过退相干过程令其自旋相互作用消失，最终使两个T1态激子转变为相互独立的T1激子，即公式(1)中的(T1+T1)态. 因此，新的激子裂变演化过程可以用一个改进的三步四状态演化模型来描述[6]：

    其中：k-2，k2，kD，kC，k-1，k1为不同状态间相互转化的速率. 值得注意的是，对公式(2)中新增的中间过渡态1(T…T)，已有的实验报道不多，所涉及的材料种类也比较少，尚缺乏更多、更广泛的实验证据支持.

    在有机半导体分子上，由于电子和空穴之间存在自旋交换相互作用，导致三重态激子的能量低于单重态激子的能量. 而在某些特殊的有机分子上，特别是多并苯及其衍生物材料，三重态激子的能量刚好非常接近于单重态激子能量的一半，研究发现这类分子都能发生激子裂变过程[2]. 故激子裂变的基本条件为：S1态激子的能量E(S1)应当与两个T1态激子的能量2E(T1)相等或相近，即E(S1) ≈2E(T1)[4]. 例如，在红荧烯(rubrene, Rub)材料中，其E(S1)=2.23 eV，2E(T1)=2.28 eV，二者间的能量差ΔE=2E(T1)-E(S1)仅有50 meV[9]. 为了验证1(T…T)中间过渡态在激子裂变演化过程中的重要性，本实验以红荧烯材料为研究对象，在不同温度下测量了红荧烯薄膜的光致发光谱及其瞬态发光衰减曲线. 而后，基于两步三状态演化模型和三步四状态演化模型，分别利用两组耦合的微分方程组对不同温度下的发光衰减曲线进行理论拟合. 曲线拟合结果显示，相较于两步三状态演化模型，三步四状态演化模型所得的拟合曲线与实验曲线的符合度更好. 进一步地，通过对拟合过程中所得的速率参数(k-2与k2)进行指数拟合，可得到前述的能量差ΔE. 速率拟合结果同样显示，相较于两步三状态演化模型，基于三步四状态演化模型所得ΔE值更接近准确值.

2.   实验结果与分析

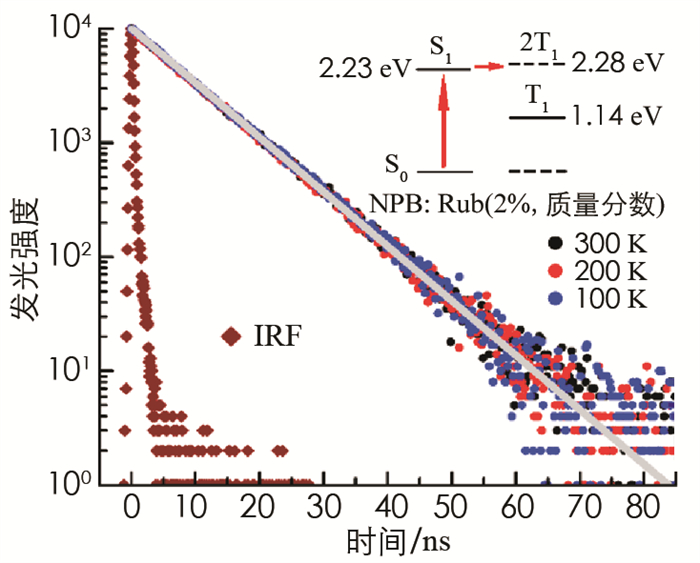
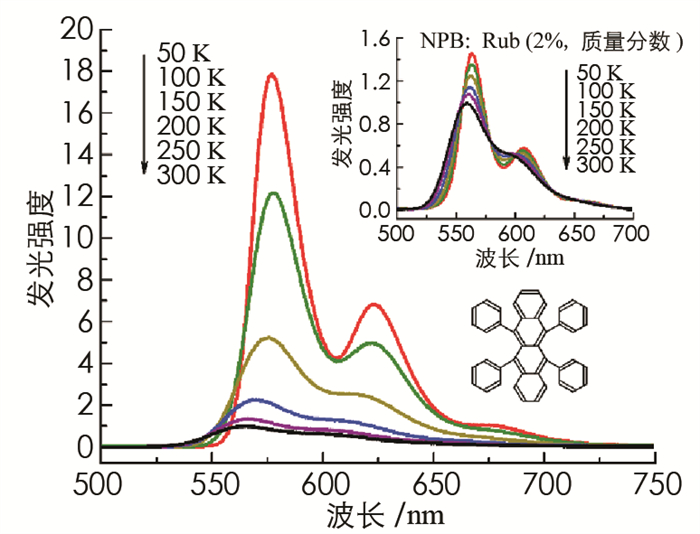
  • 使用LN-1123SC型有机/金属复合多源蒸发系统，在高真空(~1×10-5 Pa)条件下在石英玻璃衬底上蒸镀100 nm厚的纯红荧烯薄膜，在蒸发过程中衬底始终保持在室温，因此制备的薄膜样品均为非晶态结构. 样品被保存在一个低真空(~1×10-2 Pa)的容器中，并在24 h内完成实验测量. 使用Edinburgh FL920型稳态/瞬态光谱仪在不同温度下(300，250，200，150，100，50 K)分别测量了红荧烯薄膜的光致发光谱及其瞬态发光衰减曲线. 由于红荧烯分子的E(S1)<2E(T1)，故红荧烯分子间的激子裂变过程是一个吸热过程，需要吸收分子振动的能量来补偿50 meV的能量欠缺. 当温度降低时分子振动减弱，激子裂变过程被抑制，使S1态激子有更大的概率通过辐射复合方式衰减，因而造成薄膜的光致发光强度随温度降低而显著增强，图 1展示的测量结果与预期一致. 插图展示了NPB：Rub(2%，质量分数)掺杂薄膜在不同温度下的光致发光谱，虽然随温度降低发光峰与纯红荧烯薄膜一样变得更尖锐，但发光谱线下的面积基本不变.

    为了对样品的发光衰减过程进行理论拟合，需要知道红荧烯分子中S1态激子的发光速率kS，为此特别制备了NPB：Rub(2%，质量分数)掺杂薄膜，并在不同温度下测量了掺杂薄膜的瞬态发光衰减曲线. 在掺杂薄膜中，NPB分子起到间隔作用，目的是将红荧烯分子分开，由于红荧烯分子处于非常稀释的状态，相邻红荧烯分子间距离太大，不能发生激子裂变过程，光激发的S1态激子只能通过辐射复合的方式退激. 如图 2所示，掺杂薄膜发光强度的衰减正比于指数函数exp(-kSt)，由此可确定红荧烯分子S1态激子的发光速率kS，指数拟合得到kS=0.11 ns-1，对应S1态激子的平均寿命约9.1 ns. 图 2还展示了测量仪器的响应函数(instrumental response function, IRF)曲线，该曲线的半高宽仅有0.63 ns，远小于S1态激子的平均寿命，表明测量仪器的时间分辨能力对测量结果没有影响. 图 2中的插图为红荧烯分子发生激子裂变过程的能级跃迁示意图. 此前已有诸多关于红荧烯材料中激子裂变过程的实验研究，其研究对象大多为晶态红荧烯，由于晶态红荧烯的载流子迁移率高，故晶态材料中的激子裂变过程速度超快，从(S1+S0) 态向1(TT)i态的转变仅需~200 fs[9]，这远远超出了本实验所用FL920型瞬态光谱仪的响应速度(~0.63 ns). 而对于非晶态红荧烯，由于材料的载流子迁移率大大降低，激子裂变过程的所需时间延长到ns量级，已经低于光谱仪的响应速度. 故本实验以热蒸发得到的非晶态红荧烯薄膜材料为激子裂变过程的研究对象. 在科学研究中，对实验结果进行理论拟合或数值分析是一种常用的研究方法[10]. 2013年，Piland等[11]曾采用(S1+S0)↔(T1+T1)单步两状态反应模型来拟合非晶态红荧烯的激子裂变过程. 由于该模型过于简化，拟合曲线几乎完全无法和实验曲线重合，除本课题组外，其他类似的工作未见报道.

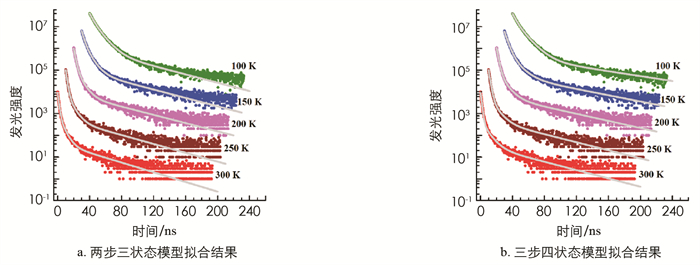
    基于两步三状态演化模型，可列出耦合的微分方程组来对发光的衰减过程进行描述.

    其中：NS为S1态激子的数量，ND为中间过渡态1(TT)i的数量，NT为(T1+T1)态激子对的数量，kS为S1态激子辐射复合的速率，kT为T1态激子非辐射复合的速率. 曲线拟合时，设定合适的初始值NS(0)，ND(0)，NT(0)和速率值(k-2，k2，k-1，k1，kS，kT)，即可根据方程组(3)进行迭代运算，得到各个时刻NS(t)，ND(t)和NT(t)的值，而薄膜的光致发光强度正比于NS(t)，即用NS(t)随时间的变化代表光致发光强度的变化. 拟合结果展示在图 3a中. 类似地，再次基于三步四状态演化模型，可列出耦合的微分方程组来对发光的衰减过程进行描述.

    其中：ND1为1(TT)i态的数量，ND2为1(T…T)态的数量，其他各相关量的设定与方程组(3)相同. 再次设定合适的初始值NS(0)，ND(0)，NT(0)和速率值(k-2，k2，kD，kC，k-1，k1，kS，kT)，拟合方法同上，拟合结果展示在图 3b中.

    在图 3a中，由方程组(3)算得的拟合曲线和实验曲线均只能在0~100 ns的时间范围内符合得很好，超过100 ns以后拟合曲线几乎都以相同的趋势快速衰减，明显偏离实验曲线. 而在图 3b中，除了300 K和250 K对应曲线较之两步三状态模型改善较小外，其余3条曲线的拟合结果都与实验曲线符合得更好. 这些差异说明，公式(1)和方程组(3)对激子裂变过程及其逆过程的描述不够细致，而公式(2)和方程组(4)对激子裂变过程的描述更加合理，中间过渡态1(T…T)的加入使得演化过程更符合实际情况，因而拟合曲线和实验曲线的符合度更好，这从实验角度证实了1(T…T)态的重要性.

    在2015年，Scholes[6]通过分支图解法(branching diagram method)对双分子态中各分子上的电子排列方式进行了描述，他对形成的各双分子态的波函数和分离后的波函数，以及双分子态能量的理论计算结果进行分析后提出，耦合形成的双分子态即1(TT)i态，可通过T1-T1能量转移机制(triplet-triplet energy transfer)先经过空间上的分离，即两个分子间电子云交叠程度开始消减直至消失，但还保持着自旋相互作用，然后再经过自旋退相干使两分子完全分离. 在2016年，Pensack等[7]从实验角度证实需要一个新的中间过渡态加入到激子裂变过程的演化模型中，并指出1(T…T)态的瞬态吸收信号与T1态激子的吸收信号很类似，而与1(TT)i态的吸收信号相异. 这是因为，在1(TT)i态中两个相互耦合的T1激子之间有较强的相互作用，而在1(T…T)态中这种相互作用由于T1激子的空间分离而大大减弱，同时分离前后分子的电子云密度也发生了明显变化，这使得裂变分子在电子振动结构部分特定波长范围内对应的吸收谱线的形状发生变化，因而可以从瞬态吸收谱中辨识出两个中间过渡态各自的吸收信号，并对他们的动态变化进行追踪.

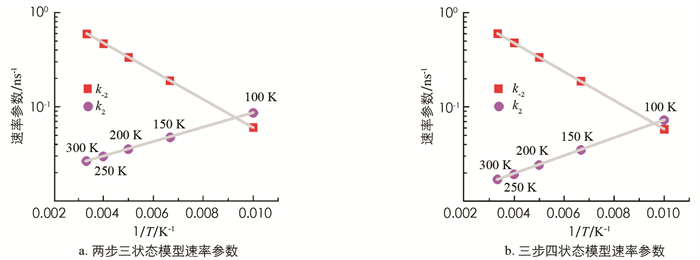
    如果采用化学反应理论对激子裂变的演化过程进行分析，对于激子裂变和激子聚变这样共存的可逆反应，根据分子反应的动力学理论，反应速率满足下述特点[12]. 一方面，由于红荧烯分子间的激子裂变为吸热过程，故速率k-2满足Arrhenius定律，即k-2=A·exp(-E-2/kBT)，其中kB为玻尔兹曼常数，T为热力学温度，参数A为频率因子，在100~300 K范围内，通过对k-2-1/T的拟合即可得到激发能量E-2. 另一方面，速率k2可表示为k2=B·exp(E2/kBT)，在100~300 K范围内，同样可通过对k2-1/T的拟合得到特征能量值E2. 根据细致平衡原理，速率k-2与k2两者间满足关系：k-2/k2∝exp(-ΔE/kBT)，其中ΔE即为能量差值2E(T1)-E(S1). 对红荧烯材料，已实验测得ΔE=50 meV[9]. 本研究对瞬态发光衰减曲线拟合使用的速率k-2和k2的值进行了指数拟合，拟合结果展示在图 4中. 由图 4a展示的拟合结果得到E-2≈29.5 meV，E2≈15.5 meV，则ΔE=E-2+E2≈45 meV. 由图 4b展示的拟合结果得到E-2≈30 meV，E2≈19 meV，则ΔE=E-2+E2≈49 meV. 由此可见，利用两步三状态演化模型对红荧烯中的激子裂变过程进行拟合，最终得到的ΔE与准确值相差5 meV，而利用三步四状态演化模型进行拟合，最终得到的ΔE与准确值仅相差1 meV，这再次说明利用三步四状态模型对激子裂变过程进行描述更加合理.

3.   结论

  • 理论上，基于激子裂变传统的两步三状态演化模型和新的三步四状态演化模型可各自列出一组耦合的微分方程组，通过各参数之间的迭代运算，得到各个激发态数量随时间的变化，再由S1态激子数量随时间的变化即可得到理论上的瞬态衰减过程. 一方面，拟合曲线和实验曲线的符合程度显示，用三步四状态演化模型来描述激子裂变的演变过程要比两步三状态演化模型更合理. 另一方面，对速率参数的指数拟合结果同样显示，相较于两步三状态模型，通过三步四状态模型得到的激子裂变能量差值更接近准确值. 这两方面的结果从实验角度证实了中间过渡态1(T…T)在演化模型中的重要性.

参考文献 (12)

目录

版权所有：西南师范大学学报(自然科学版)

地址：重庆市北碚区西南大学 电话：023-68252540，68254576，68254478 电子邮箱：xbbjb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回