-
在能源危机及环境污染日益严重的情况下,发展提高能源利用效率的应用技术愈发紧迫.石墨烯材料具有高导热、高热容等性能,作为一种超高热传导和大热容材料,在制作各类超薄型散热片和散热涂层、高蓄热等材料、器件以及可调节热管理系统等方面有广泛的应用.在应用中,都涉及到它的热容量、热导率等性能随温度变化的规律以及蓄热传热稳定性问题,目前已有不少文献对此问题进行了研究. 2008年,Balandin等[1]采用非接触的光学技术(non-contacat optical technique),用实验测得石墨烯的热导率为(4.84±0.44)×103~(5.30±0.48)×103 W/(m·K);2009年,Nika等[2]采用第一性原理计算得到石墨烯的热导率在2 000~6 000 W/(m·K)之间;2010年,Lindsay等[3]实验测出10 μm厚的石墨烯热导率随温度的变化关系.此后,Bagri等[4-6]用实验和密度泛函理论第一性原理、蒙特—卡罗法对非平衡态下晶界、应变效应以及磁场对石墨烯热容量和热导率等的影响进行了研究;Liu等[7-8]研究了石墨烯在空气中的热稳定性;2017年,Ali和Amin等[9-10]分别对纳米流体对水基石墨烯纳米片传热性能的影响和蜂蜡/石墨烯相变材料作为建筑用储能材料的热性能稳定性进行了研究;2018年,Nazari等[11]又对氧化石墨烯纳米流体对脉动热管增强传热的稳定性进行了实验研究,这些研究揭示了石墨烯蓄热和传热的一些特点,但未给出它们随温度变化规律的解析式,对热性能稳定性也仅定性提及.为了定量探讨其变化规律,2016年,Ren等[12]考虑到原子非简谐振动,用固体物理理方法,研究了石墨烯德拜温度、热容量和热导率等随温度变化规律及其影响因素,但计算中仅考虑到原子非简谐振动项对德拜温度的影响,未考虑对自由能等的影响,得到的热容量与实验有差距,而且未研究热稳定性问题. Podlivaev等在文献[13]中指出:石墨烯在能源工程传热,高效能源收集、存储和转换的应用中,形状变化和机械弯曲等必然发生而影响传热和蓄热性能的稳定性.特别是在散热蓄热设备长期暴露于温度变化的高温环境,石墨烯的比表面积很大,对温度等外界环境的变化极为敏感,从理论上深入探讨石墨烯蓄热和传热等性能随温度的变化规律和热稳定性,是理论和应用上亟待解决而至今还少见报导的重要问题.本研究将考虑到原子非简谐振动对德拜温度和自由能等的影响,用固体物理理论,研究石墨烯蓄热传热性能热稳定性随温度变化的规律,探讨原子非简谐振动对它们的影响.
全文HTML
-
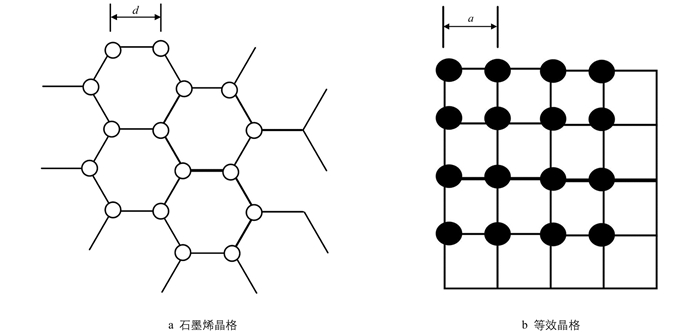
石墨烯是由碳原子构成的二维六角格子平面系统(图 1).
原子质量为M,设总原子数为N,键长为d,面积为A.考虑到原子短程相互作用,一个原子的平均相互作用能为[14]
式中:V1为金属化能,V2为共价能,d为键长;β2为结构参量,β2=2/3. R0是与短程作用有关的参量:R0=0.154×104(ћ2/2m)a012,a0为玻尔半径,m为自由电子质量.
在原子相互作用下,原子在平衡位置作非简谐振动.将φ(d)在平衡位置d0附近展开,偏离δ=d-d0很小时,有
$\varphi(\delta)=\varphi\left(d_{0}\right)+\frac{1}{2} \varepsilon_{0} \delta^{2}+\varepsilon_{1} \delta^{3}+\varepsilon_{2} \delta^{4}+\cdots, \varepsilon_{0}, \varepsilon_{1}, \varepsilon_{2}$ 分别是原子振动的简谐系数和第一、第二非简谐系数,由(1)式求得.
-
吕桂英等[15]指出,材料在热、光、化学等内外因素作用下,性能逐渐降低,甚至完全丧失使用价值,这种现象叫材料的老化(ageing).殷茜等[16]对有机PTC材料稳定性的研究表明:材料的老化一方面造成材料热阻的温度梯度增大,使加热控温性能或工作温度下降,失去使用价值,减短使用寿命;另一方面老化造成材料热阻的温度梯度减小,使材料热阻值迅速跌落,出现所谓负温度系数(negative temperature coefficient,NTC)现象,温升至一定温度时,材料热阻突然下降,可能发生烧毁材料的事故.与有机热敏电阻(positive temperature coefficient,PTC)材料类似,石墨烯在长期使用的过程中,即使没有化学反应等因素的影响,材料的老化也会造成蓄热传热的热不稳定性.
除材料老化以及材料掺杂、缺陷等会影响石墨烯蓄热传热性能的稳定性外,温度也是一个重要因素.原子的非简谐振动和温度的变化引起膨胀或收缩,使其原子组成结构和相互作用发生变化,从而导致石墨烯自由能发生改变,进而引起热容量及热阻率等蓄热传热性能发生改变.
热稳定性常用温度稳定性来描述,它反应了物理量随温度的波动情况[16].为了描述石墨烯蓄热传热性能的温度稳定性,本研究采用国外普遍采用的温度系数表示:设系统的性能参数为f,温度系数定义为αf=(1/f)(df/dT),αf愈小,性能愈稳定.
-
特性函数是指能代表系统热力学特性的函数,对面积为A、温度为T的石墨烯,自由能F(T,A)是一个特性函数.设石墨烯是2N个彼此独立的做非简谐振动的振子体系,每个自由度的振动量子化能级[17]为
这里
$\beta = {\rm{ћ}}\omega + 6{\varepsilon _2}{\left( {\frac{{\rm{ћ}}}{{2M\omega }}} \right)^2} - \frac{{30\varepsilon _1^2}}{{{\rm{ћ}}\omega }}{\left( {\frac{{\rm{ћ}}}{{2M\omega }}} \right)^3} = {\rm{ћ}}\omega + \mathit{\Delta }\beta $ ;n=0,1,2,…,∞,Δβ是非简谐项对能量量子的贡献.由(2)式求得一个自由度的振动自由能f(ω,T).蓄热传热的实际问题中,温度不太高,对石墨烯可采用二维德拜模型,晶格振动模式密度g(ω)=4N/ωD2(ω
$ \prec $ ωD);g(ω)=0(ω$ \succ $ ωD). ωD为德拜频率,与德拜温度θD关系为:ћωD=kBθD.考虑到非简谐效应后,θD与温度的关系为[12]这里θD0是T=0 K时的德拜温度,由kBθD0=ћ(8ε0/3M)1/2求得.
将g(ω)代入求自由能F的公式,得到考虑到原子非简谐振动对德拜温度和自由能的影响后,自由能为简谐近似振动自由能F0与非谐项贡献的ΔFτ以及结合能Nu(A)之和,即:
式中:
将(3)代入αF=(1/F)(dF/dT),得到石墨烯自由能热稳定性温度系数随温度等的变化.
-
石墨烯蓄热性能由热容量cV表征,由定容热容量与自由能的关系,由(4)式得
其中,cV0和ΔcV分别为简谐近似的热容量和非谐项贡献的热容量,分别表示为:
将(5)式代入
求得石墨烯蓄热稳定性的温度系数αC.
-
石墨烯传热性能由热导率K(或热阻率ρq(ρq=1/K)描述,它随温度的变化[12]为
式中:R为气体普适常数,μ为摩尔质量,v是平均声速,η是与物质有关的参数(取2),l0是平均自由程,
$ $ 是以θD/T为变量的二维德拜函数:石墨烯传热的稳定性取决于热阻率ρq的温度梯度.为了确定热阻温度梯度与温度等的关系,设热量沿平面x方向流动,热阻率为ρq,则沿热流方向x处热阻的温度梯度为:
其中dρq/dK由ρq=1/K求得.为了求得K与传热距离x的关系,引入等效晶格的概念:若边长x、晶格常数为a的正方格子,总面积和原子数与键长为d、原胞面积为Ω、原子数为N的六角形格子的石墨烯晶格(图 2a)相同,则此正方格子称为石墨烯的等效晶格.原子数N=16,面积A=16Ω的石墨烯的等效正方格子见图 2b.
由此定义,求得传热距离
$x = {(N\sqrt 3 /2)^{1/2}}d$ .由于热导率与声子平均自由程l成正比,而l与传热距离x成正比,令l0=λx,代入(7)式后再代入(8)式,求得石墨烯热阻率ρq的温度梯度$\nabla {T_x} = {\rm{d}}T/{\rm{d}}x$ 随温度的变化为式中:αl为线膨胀系数,d0为平衡时键长.
由温度系数的定义式得到描述传热性能热稳定性的温度系数
$\alpha_ {\nabla T}$ 为
3.1. 石墨烯的自由能及热稳定性系数随温度的变化
3.2. 石墨烯蓄热稳定性系数随温度的变化
3.3. 石墨烯传热稳定性系数随温度的变化
-
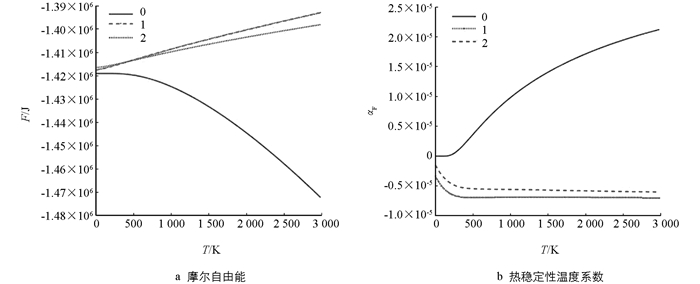
文献[14]给出:d0=1.42×10-10 m,V2=12.32 eV,V2=12.32 eV,由此求得ε0=3.257 15×102 J/m2,ε1=-1.920 15×1013 J/m3,ε2=4.919 7×1023 J/m4.碳原子质量M=1.995 017×1023 kg,求得θD0=1 660 K.取1 mol石墨烯作计算,由(1)式求得内能Nu(A)=-1.429 4×106 J.将这些数据以及普朗克常数ћ、玻尔兹曼常数kB等代入(4)式,得到石墨烯的摩尔自由能随温度的变化曲线(图 3a),图中的曲线0,1,2分别是简谐近似、考虑到第一非谐项、同时考虑到第一、二非简谐项的结果.将上述数据代入(4)式,再代入热稳定性定义式,得到自由能热稳定性温度系数随温度的变化(图 3b).
由图 3看出:①石墨烯的自由能随温度升高而增大,但变化不大,温度由0 K升高到1 000 K时,摩尔自由能只增大0.008%;②考虑到原子非简谐振动后,自由能随温度升高而增大,而简谐近似下自由能随温度升高而减小.这不仅表明原子非简谐振动是自由能随温度升高而增大的原因,还说明只有考虑到原子非简谐振动,才能得到与温度升高,振动能(相应地自由能)增大的实际相符.此外,还可看出,温度愈高,非简谐与简谐近似的差异愈显著,即非简谐效应愈显著;③简谐近似下,石墨烯自由能的热稳定性温度系数随温度升高而增大,而考虑到非简谐项后则随温度升而减小,且当温度T>500 K时,其热稳定系数趋于定值,大小为-7×10-6,表示在室温以上的非低温情况石墨烯热学性能是非常稳定的,即使升温1 000 K,热学性能只变化1‰.
-
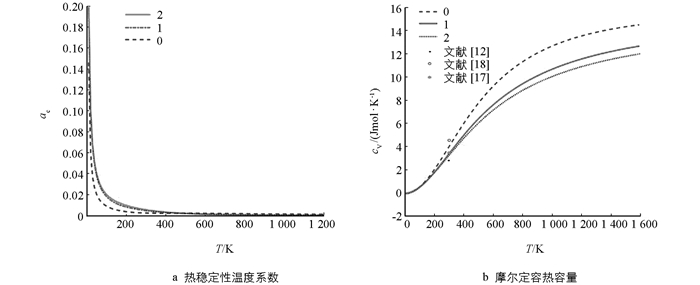
将上述数据代入(5)式和(6)式,得到石墨烯蓄热稳定性系数αC随温度的变化(表 1),其变化曲线见图 4a,图中的曲线0,1,2分别是简谐近似、只考虑第一非简谐项和同时考虑第一、第二非简谐项的结果.为了说明本研究同时考虑到非简谐振动项对自由能等的影响与文献[12]只考虑到对德拜温度θD的影响的结果的差异,图 4b给出了摩尔定容热容量(N=16)随温度的变化(表 2).图中,曲线0,1,2意义同前,而图中记号分别是文献[12]只考虑到非简谐项对德拜温度θD的影响的结果和文献[17]基于密度泛函理论的第一性原理的计算结果,以及文献[18]使用晶格动力学的结果.
由表 1、表 2和图 4看出:①石墨烯的摩尔定容热容量随温度升高而非线性增大,温度较低(如T<200 K)时增大得较快,温度较高(如T>1 300 K)时变化较慢,温度更高时,则趋于常量;②石墨烯蓄热量很大且蓄热稳定性很好.如在T=300~1 000 K的温度范围内,热容量可达4.012~12.670 J/(mol·K),而温度系数仅在0.020 0~0.001 3之间;③温度低于150 K时,石墨烯蓄热稳定性随温度升高而迅速减小;温度高于150 K时,则变化极小并趋于零.这表示:高于室温以上的温度下,石墨烯蓄热稳定性非常好,热容量几乎不随温度而变;④非简谐项对石墨烯的蓄热性质和蓄热稳定性有一定的影响:它使热容量的值稍小于简谐近似时的值,对热容量的影响|Δcv|/cv在1.2%~1.4%之间并随温度升高而增大,而对蓄热稳定性的影响只在100~300 K的温度范围较明显(1.2%~2.5%);⑤本研究得到的热容量的值比仅考虑对德拜温度影响的值更接近实验及文献[18]用晶格动力学的结果.
-
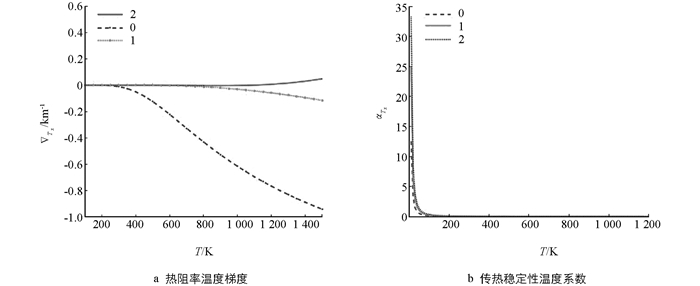
传热稳定性由热阻率温度梯度
$\nabla {T_x}$ 稳定性温度系数${\alpha _{\nabla {T}}}$ 描述.将上述数据代入(9)-(10)式,得到石墨烯的$\nabla {T_x}$ 以及${\alpha _{\nabla {T_x}}}$ 随温度的变化(图 5a和图 5b). 图 5中,曲线0,1和2分别是简谐近似、考虑到第一非简谐项和同时考虑到第一、第二非简谐项的结果.由图 5可看出:①在温度较低(T<200 K)时,石墨烯的传热稳定性差.热阻率温度梯度虽很小但传热稳定性温度系数随温度变化却较大,温度从50 K变到200 K时,传热稳定性温度系数从0.134 8变为0.036 9,减小了72.6%;而T=300~1 000 K的温度范围内,石墨烯的导热稳定性好:热阻率温度梯度和传热稳定性温度系数都几乎趋于零;②非简谐振动项对石墨烯传热稳定性有重要影响:简谐近似或只考虑到第一非简谐项时,得到的热阻率温度梯度随温度升高而减小,与事实不符,同时考虑第一、第二非简谐项时,能得到较正确的结果;考虑到非简谐项时得到的传热稳定性温度系数要比简谐近似的值稍大.
4.1. 石墨烯自由能及其热稳定性温度系数
4.2. 石墨烯蓄热稳定性温度系数随温度的变化
4.3. 石墨烯传热稳定性温度系数随温度的变化
-
本研究考虑到原子非简谐振动,用固体物理理论和方法,对石墨烯的自由能以及蓄热和传热稳定性随温度的变化规律进行研究,结果表明:①温度低于300 K时,自由能以及热容量、热导率的热稳定性温度系数都很大且随温度升高而急剧变小,石墨烯的蓄热和传热的热稳定性差;②在300~1 000 K的温度范围内,自由能以及热容量、热导率的热稳定性温度系数都很小,在0.020 0~0.001 3之间,随温度升高而缓慢地非线性变小,并随温度继续升高而趋于0,石墨烯蓄热和导热的热稳定性好;③原子非简谐振动对石墨烯自由能和它的热稳定性有重要的影响.简谐近似下,自由能随温度升高而减小,热稳定性随温度升高而增大,考虑到非简谐项后情况相反;④非简谐和简谐近似下石墨烯的蓄热和传热稳定性随温度的变化规律相似,但非简谐的值大于简谐近似的值;⑤考虑到非简谐项对自由能等的影响,其结果比文献[12]只考虑到对德拜温度影响的结果,与实验和其他文献结果更接近.



 下载:
下载: