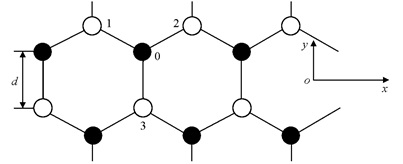
本研究采用的计算模型见图 1，图 1中黑色原子(Al原子)和白色原子(N原子)构成二维六角格子平面系统.设Al原子和N原子数均为n，最近邻原子间距离为d，取任一原子为坐标原点，平面为oxy平面(图 1)，z轴垂直纸面向外.

平衡状态下AlN单层膜中一个原子的平均相互作用能为^[15]

其中：V₁为金属化能；C=0.20 eV，用来描述短程作用^[15]；V₂和V₂^*分别为σ键和π键的共价能，V₂^*=η₂ћ²/md²，V₂^*=η_ppπћ²/md²，这城d是最近邻原子间距离，ћ是普朗克常数，m是自由电子的质量.因为AlN单层膜为典型的sp²杂化，所以η=3.22，η_ppπ=0.63^[15]. α_c和α_c^*分别是σ键和π键的共价参量，定义为：

另外，σ键和π键的极性参量定义为：

其中：V₃和V₃^*分别为σ键和π键的极化能.

T=0 K时各原子静止在平衡位置，键长为d₀.任意温度下，键长为d，对平衡位置的位移为δ=d-d₀.因热运动，原子在平衡位置沿键长方向作非简谐振动.将相互作用势展开为级数，则$\varphi (\delta ) = \varphi (0) + \frac{1}{2}{\varepsilon _0}{\delta ^2} + {\varepsilon _1}{\delta ^3} + {\varepsilon _2}{\delta ^3} + \cdots $.第2项为简谐项，第3项后各项分别称为第1、第2、……非简谐项，ε₀，ε₁，ε₂，……分别称为简谐系数和第1、第2、……非简谐系数，由(1)式可得：

一般情况下d(T)=d₀+δ(T)，其中原子平均位移δ(T)和线膨胀系数α_l=(1/d₀)(dδ/dT)分别为^[19-20]：

T=0 K时，σ键和π键的共价能、极性参量和共价参量中原子间距均取d₀.非零温情况下，因原子非简谐振动，键长变为

使得σ键和π键的共价能变为

将(10)式代入(3)式可求出极性参量和共价参量随温度的变化关系，从而由(1)式可得到类石墨烯的键能随温度的变化为

德拜温度是二维材料热学性质的一个重要特征量.文献[21]给出简谐近似下二维六角结构的德拜温度θ_D0与简谐系数ε₀的关系为

其中：M为折合原子量，M^-1=M_Al^-1+M_N^-1，M_Al和M_N分别为Al和N的原子量. (12)式中未考虑非简谐效应的影响，因而不能反映德拜温度的实际变化规律.利用振动频率ω与温度的关系式，可得到德拜温度θ_D与温度T的关系为^[19]

按照晶格热容的德拜理论，对由N个原胞组成的二维晶格，定容热容量为^[20]

而定容比热为

式中：μ为折合摩尔质量，μ^-1=μ_Al^-1+μ_N^-1，μ_Al和μ_N分别是Al和N的摩尔质量.

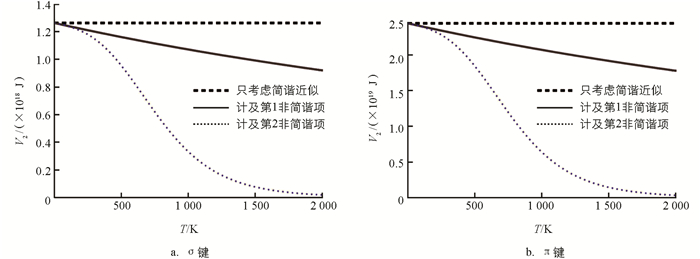
文献[15]给出了AlN单层膜T=0 K时的几个参数，分别为d₀=1.78×10^-10 m，V₁=3.15 eV，V₂=7.84 eV，V₃=1.52 eV，V₂^*=5.30 eV和V₃^*=0.98 eV.相应地，可算出T=0 K时的极性参量α_p=0.56和共价参量α_c=0.83.将这些数据以及C=0.20 eV代入(5)、(6)、(7)式，可求得AlN单层膜原子振动的几个参数：ε₀=0.507×10² J/m²，ε₁=-0.947×10¹² J/m³和ε₂=-0.225×10²² J/m⁴.将这些数据代入(10)式，可得到AlN单层膜σ键和π键的共价能随温度的变化(图 2)，图 2中虚线、实线和点线分别对应只考虑简谐近似、计及第1非简谐项、计及第2非简谐项的结果.

由图 2看出，如果只考虑到简谐项，AlN单层膜σ键和π键的共价能均与温度无关；考虑到第1非简谐项，它们随温度升高而线性减小；考虑到第2非简谐项，它们随温度升高非线性减小.在500~1 500 K的温度范围变化较快，表明温度愈高，非简谐效应愈显著.超过1 500 K，变化逐步趋缓，最终平稳.

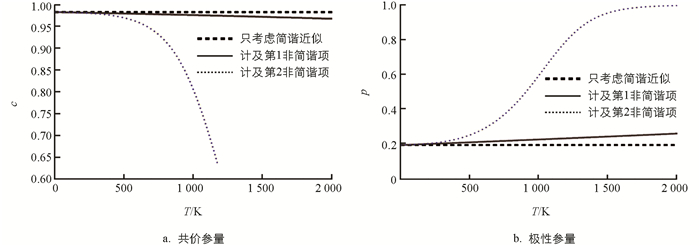
将上述数据代入(3)式，可得到AlN单层膜σ键的共价参量和极性参量随温度的变化(图 3)，图 3中虚线、实线和点线分别对应只考虑简谐近似、计及第1非简谐项、计及第2非简谐项的结果.

由图 3看出，简谐近似下，σ键的共价参量和极性参量均不变；只计及第1非简谐项时，共价能随温度升高而线性地缓慢变化；计及第2非简谐项时，共价参量随温度升高非线性减小.相反地，极性参量随温度升高而非线性增大.在400 K以下，共价参量变化极小，几乎保持为0.982，导致极性参量变化也极小，几乎保持为0.189.在400~1 500 K的温度范围变化较快，温度愈高，非简谐效应愈显著.高于1 500 K后逐步趋于稳定，T=2 000 K时共价参量约为0，从而使得极性参量接近于稳定值1.

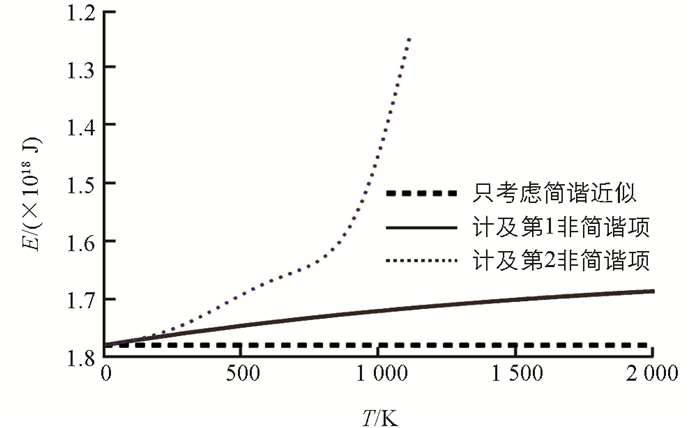
由(11)式，可得到AlN单层膜的键能随温度的变化(图 4)，图 4中虚线、实线和点线分别对应只考虑简谐近似、计及第1非简谐项、计及第2非简谐项的结果.

由图 4看出，如果只考虑到简谐项，AlN单层膜σ键的键能与温度无关，保持为-1.800×10^-18 J；考虑到第1非简谐项后，键能随温度升高而线性地缓慢增加；考虑到第2非简谐项，在极低温下(低于150 K)，键能随温度的变化与只考虑到第1非简谐项相近，表明极低温下第2非简谐效应的影响较小.高于150 K后，键能随温度升高非线性增大，且温度愈高，变化越大，表明非简谐效应愈显著.

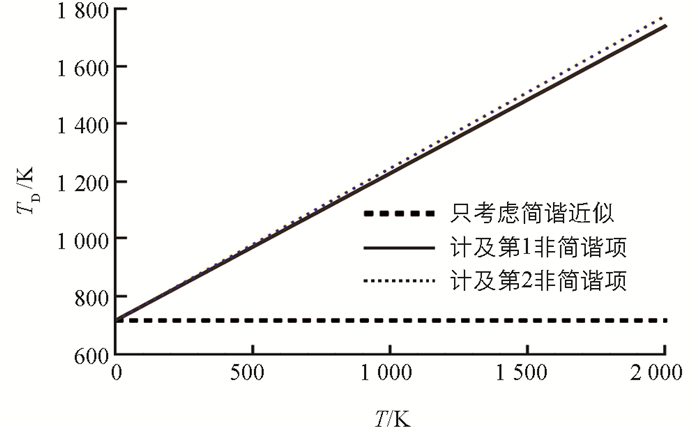
将Al和N的原子量27和14个原子量单位与ε₀，ε₁，ε₂代入(13)式，可得到AlN单层膜的德拜温度随温度的变化(图 5)，图 5中虚线、实线和点线分别对应只考虑简谐近似、计及第1非简谐项、计及第2非简谐项的结果.

由图 5看出，简谐近似下，AlN单层膜的德拜温度与温度无关，始终为716.887 K.考虑到第1和第2非简谐项后，德拜温度均随温度升高而线性增大，表明温度愈高，非简谐效应愈显著.另外，此两种情况下的德拜温度差Δθ_D=θ_D2-θ_D1随着温度升高而增大.例如，T为0，500，1 000，1 500，2 000 K时，Δθ_D分别为0.000，8.660，17.319，25.978，34.638 K，表明第2非简谐效应对德拜温度的影响略大于第1非简谐效应，且温度越高，第2非简谐效应的影响越明显.实际上，德拜温度是反映材料中原子间结合力的一个重要物理量，德拜温度和原子振动频率上限成正比.一般地，德拜温度越高，原子间作用力越大，杨氏模量越大，振动频率越高.对AlN单层膜，温度越高，原子振动越强，因此振动频率越大，原子振动时偏离平衡位置的位移越大，使得非简谐效应随温度的升高越来越明显，从而导致了德拜温度随温度的变化逐步增大.因此，考虑第1和第2非简谐效应对应的德拜温差也随温度的升高而变大.

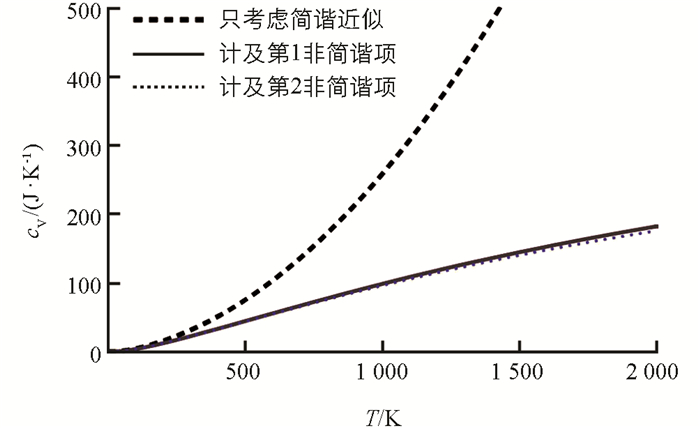
由(15)式可得到AlN单层膜定容比热随温度的变化(图 6)，图 6中虚线、实线和点线分别对应只考虑简谐近似、计及第1非简谐项、计及第2非简谐项的结果.

由图 6可看出，只考虑简谐效应时AlN单层膜的定容比热随温度的升高非线性地增大.一般地，定容热容量在温度较高时会趋于稳定，即随温度的变化逐步趋缓.因此，只考虑简谐效应，计算值与实际相差较大.当考虑到非简谐项后，AlN单层膜的定容比热在低温下与只考虑简谐效应时较为接近，但当温度高于200 K后，非简谐效应与简谐近似对应的定容比热的差Δc_v=c_v0-c_v随温度升高而增大，即非简谐效应愈显著.尤其是，温度比较高时，非简谐效应对应的定容比热随温度的变化趋缓，逐步接近稳定，与实际比较相符.例如，T=1 000 K时，考虑非简谐效应后定容比热约为99.93 J/K，与第一性原理计算的三维AlN的定容比热以及实验值极为接近^[22-23]，而非简谐效应近似对应的高达260.55 J/K则相差极大.另外，考虑到第2非简谐项对应的值总是略低于只考虑第1非简谐项.表明二阶非简谐效应对定容比热有一定影响.

基于上述研究可知，①研究相关热学参量时应考虑非简谐效应，温度越高，非简谐效应的影响越明显，第2非简谐效应的影响越显著. ② AlN单层膜的σ键和π键的共价能、共价参量和极性参量均随温度呈非线性变化，在500~1 500 K的温度范围变化较快，高于1 500 K，变化逐步变缓，最终平稳. ③在极低温下，键能随温度升高而线性地增大，高于150 K后，键能随温度升高而非线性地增大，且温度愈高，非简谐效应愈显著. ④德拜温度随温度升高而线性地增大. ⑤温度不太高时，定容比热随温度升高而线性地增大，温度较高时，定容比热随温度的升高逐步变缓.