高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

多通道特征向量的新三角距离高效推荐

,  ,  , 

上一篇

下一篇

吕亚兰, 张恒汝, 秦琴, 等. 多通道特征向量的新三角距离高效推荐[J]. 西南大学学报（自然科学版）, 2021, 43(10): 19-28. doi: 10.13718/j.cnki.xdzk.2021.10.003
引用本文: 吕亚兰, 张恒汝, 秦琴, 等. 多通道特征向量的新三角距离高效推荐[J]. 西南大学学报（自然科学版）, 2021, 43(10): 19-28. doi: 10.13718/j.cnki.xdzk.2021.10.003
shu
LYU Yalan, ZHANG Hengru, QIN Qin, et al. Efficient Recommendation of New Triangular Distance for Multi-channel Feature Vectors[J]. Journal of Southwest University Natural Science Edition, 2021, 43(10): 19-28. doi: 10.13718/j.cnki.xdzk.2021.10.003
Citation: LYU Yalan, ZHANG Hengru, QIN Qin, et al. Efficient Recommendation of New Triangular Distance for Multi-channel Feature Vectors[J]. Journal of Southwest University Natural Science Edition, 2021, 43(10): 19-28. doi: 10.13718/j.cnki.xdzk.2021.10.003
shu

多通道特征向量的新三角距离高效推荐

  • 西南石油大学 计算机科学学院, 成都 610500

  • 基金项目: 国家自然科学基金项目(61902328)；四川省科技厅应用基础研究项目(2019YJ0314)；四川省青年科技创新研究团队(2019JDTD0017)；浙江海洋大学大数据挖掘与应用省重点实验室开放课题(OBDMA202005)
详细信息
    作者简介:

    吕亚兰，硕士研究生，主要从事推荐系统的研究 .

    通讯作者: 张恒汝，教授; 

  • 中图分类号: TP391

Efficient Recommendation of New Triangular Distance for Multi-channel Feature Vectors

  • College of Computer Science, Southwest Petroleum University, Chengdu 610500, China

  • 摘要: 为同时提高推荐系统的准确度和效率，提出了一种多通道特征向量的新三角距离推荐算法. 首先从原始评分矩阵中提取多通道特征向量；其次结合三角距离和Jaccard系数构建新三角距离；最后将该距离用于k近邻算法以表征两个项目间的相似度. 在4个真实数据集上的实验结果表明：文中提出的算法推荐效率更高，并能保持较好的推荐准确度.
    Abstract: In order to simultaneously enhance the accuracy and efficiency of the recommender system, this paper designs a new triangular distance recommendation algorithm for multi-channel feature vectors. Firstly, we use item's rating matrix to extract multi-channel feature vectors. Secondly, we combine the triangular distance and Jaccard similarity coefficient to conduct a new triangular distance. Finally, we apply this distance to the k-nearest neighbor algorithm to characterize the similarity between two items. The experimental results on 4 real datasets show that the proposed algorithm is more efficient and better accuracy.
  • 加载中

  • 图 1  多通道特征向量的构建

    下载: 全尺寸图片 幻灯片

    图 2  4个数据集上的运行时间结果

    下载: 全尺寸图片 幻灯片

    表 1  符号系统

    符号 含义
    U 所有用户的集合
    T 所有项目的集合
    ui 第i个用户
    tp 第p个项目
    vp 项目tp的多通道特征向量
    Ip 对项目tp评过分的用户集合
    C 所有评分等级构成的集合
    l 通道数l
    R 评分矩阵
    Hp 项目tp的邻居集合
    G(tp，tq) 对第p，q个项目均评过分的用户集合
    P(tp，x) 项目tp的评分为x的概率
    rip 第i个用户对第p个项目的实际评分
    rip* 第i个用户对第p个项目的预测评分
    $\overline {r\left( { \bullet , {t_p}} \right)} $ 项目tp的评分向量
    $\overline {r\left( { \bullet , {t_p}} \right)} $ 项目tp的平均评分
    下载: 导出CSV

    表 2  评分矩阵(R)

    用户\项目 t1 t2 t3 t4 t5 t6
    u1 2 3 2 2 4 0
    u2 2 0 4 1 5 0
    u3 0 0 4 5 0 0
    u4 4 2 5 4 0 5
    u5 0 4 1 2 0 4
    下载: 导出CSV

    表 3  不同距离公式

    距离 公式 时间复杂度
    Cosine[5] ${\mathop{\rm Cosine}\nolimits} \left( {{t_p}, {t_q}} \right) = \frac{{\overrightarrow {r\left( { \cdot , {t_p}} \right)} \cdot \overrightarrow {r\left( { \cdot , {t_q}} \right)} }}{{\left| {\overline {r\left( { \bullet , {t_p}} \right)} } \right| \times \left| {\overline {r\left( { \bullet , {t_q}} \right)} } \right|}}$ O(n)
    ED[11] ${\rm{ED}}\left( {{t_p}, {t_q}} \right) = \sqrt {\mathop \sum \limits_{{u_i} \in {G_{{t_p}, {t_q}}}} {{\left( {{r_{ip}} - {r_{iq}}} \right)}^2}} $ O(n)
    BC[12] ${\rm{BC}}\left( {{t_p}, {t_q}} \right) = \sum\limits_{x \in C} {\sqrt {P\left( {{t_p}, x} \right) \times P\left( {{t_q}, x} \right)} } $ O(l)
    PCC[6] ${\rm{PCC}}({t_p}, {t_q}) = \frac{{\sum\limits_{{u_i} \in {G_{{t_p}}}, {t_q}} {\left( {{r_{ip}} - \overline {r\left( { \bullet , {t_p}} \right)} } \right)} \left( {{r_{iq}} - \overline {r\left( { \bullet , {t_q}} \right)} } \right)}}{{\sqrt {\sum\limits_{{u_i} \in {G_{{t_p}}}, {t_q}} {{{\left( {{r_{ip}} - \overline {r\left( { \cdot , {t_p}} \right)} } \right)}^2}} } \sqrt {{u_i} \in {G_{{t_p}, {t_q}}}{{\left( {{r_{iq}} - \overline {r\left( { \cdot , {t_q}} \right)} } \right)}^2}} }}$ O(n)
    MD[13] ${\rm{MD}}\left( {{t_p}, {t_q}} \right) = \sum {\left| {\overrightarrow {r\left( { \cdot , {t_p}} \right)} - \overrightarrow {r\left( { \cdot , {t_q}} \right)} } \right|} $ O(n)
    SØrensen[14-15] ${\rm{S}}\emptyset {\rm{rensen}}\left( {{t_p}, {t_q}} \right) = \frac{{\sum {\left| {\overrightarrow {r\left( { \cdot , {t_p}} \right)} - \overrightarrow {r\left( { \cdot , {t_q}} \right)} } \right|} }}{{\sum {\left| {\overrightarrow {r\left( { \bullet , {t_p}} \right)} + \overline {r\left( { \cdot , {t_q}} \right)} } \right|} }}$ O(n)
    Canberra[16] ${\rm{Canberra}}\left( {{t_p}, {t_q}} \right) = \sum {\frac{{\left| {\overrightarrow {r\left( { \bullet , {t_p}} \right)} - \overrightarrow {r\left( { \bullet , {t_q}} \right)} } \right|}}{{\overrightarrow {r\left( { \bullet , {t_p}} \right)} + \overline {r\left( { \bullet , {t_q}} \right)} }}} $ O(n)
    Lorentzian[17] ${\rm{Lorentzian}}\left( {{t_p}, {t_q}} \right) = \sum {\ln } \left( {1 + \left| {\overrightarrow {r\left( { \bullet , {t_p}} \right)} - \overrightarrow {r\left( { \cdot , {t_q}} \right)} } \right|} \right)$ O(n)
    Divergence[18] ${\rm{Divergence}}\left( {{t_p}, {t_q}} \right) = 2\sum {\frac{{{{\left( {\overrightarrow {r\left( { \cdot , {t_p}} \right)} - \overrightarrow {r\left( { \cdot , {t_q}} \right)} } \right)}^2}}}{{{{\left( {\overrightarrow {r\left( { \cdot , {t_p}} \right)} + \overline {r\left( { \cdot , {t_q}} \right)} } \right)}^2}}}} $ O(n)
    下载: 导出CSV

    表 4  数据集

    数据集 用户个数 项目个数 评分个数
    Amazon 1 094 1 673 34 120
    MovieLens943u 943 1 684 100 000
    MovieLens706u 706 8 570 100 023
    Eachmovie 72 916 1 628 2 811 983
    下载: 导出CSV

    表 5  评价指标

    指标名称 公式
    MAE[21]↓ ${\rm{MAE}} = \frac{{\sum\limits_{i = 0}^{n - 1} {\sum\limits_{p = 0}^{m - 1} {\left| {{r_{ip}} - r_{ip}^*} \right|} } }}{{|(i, p) \in \{ 0.n - 1\} \times \{ 0.m - 1\} |{r_{ip}} \ne 0\mid }}$
    RMSE[21]↓ ${\rm{RMSE}} = \sqrt {\frac{{\mathop \sum \limits_{i = 0}^{n - 1} \mathop \sum \limits_{p = 0}^{m - 1} {{\left( {{r_{ip}} - r_{ip}^*} \right)}^2}}}{{|(i, p) \in \{ 0..n - 1\} \times \{ 0..m - 1\} |{r_{ip}} \ne 0\mid }}} $
    Accuracy[22]↑ ${\mathop{\rm Acc}\nolimits} = \frac{{\left| {\left\{ {\left\langle {{u_i}, {t_p}} \right\rangle \mid {r_{ip}} > LR, r_{ip}^* > TR} \right\}} \right| + \left| {\left\{ {\left\langle {{u_i}, {t_p}} \right\rangle \mid {r_{ip}} ＜ LR, r_{ip}^* ＜ TR} \right\}} \right|}}{{\left| {r_{ip}^*} \right|}}$
    Recall[22]↑ ${\mathop{\rm Recall}\nolimits} = \frac{{\left| {\left\{ {\left\langle {{u_i}, {t_p}} \right\rangle \mid {r_{ip}} > LR, r_{ip}^* > TR} \right\}} \right|}}{{\left| {\left\{ {\left\langle {{u_i}, {t_p}} \right\rangle \mid {r_{ip}} > LR, r_{ip}^* > TR} \right\}} \right| + \left| {\left\{ {\left\langle {{u_i}, {t_p}} \right\rangle \mid {r_{ip}} > LR, r_{ip}^* ＜ TR} \right\}} \right|}}$
    Precision[22]↑ ${\mathop{\rm Pre}\nolimits} = \frac{{\left| {\left\{ {\left\langle {{u_i}, {t_p}} \right\rangle \mid {r_{ip}} > LR, r_{ip}^* > TR} \right\}} \right|}}{{\left| {\left\{ {\left\langle {{u_i}, {t_p}} \right\rangle \mid {r_{ip}} > LR, r_{ip}^* > TR} \right\}} \right| + \left| {\left\{ {\left\langle {{u_i}, {t_p}} \right\rangle \mid {r_{ip}} < LR, r_{ip}^* > TR} \right\}} \right|}}$
    F1[22]↑ ${\rm{F1}} = \frac{{2*{\rm{ Precision }}*{\rm{ Recall }}}}{{{\rm{ Precision }} + {\rm{ Recall }}}}$
    注："↓"表示该指标"越小越好"，"↑"表示该指标"越大越好".
    下载: 导出CSV

    表 6  6个评价指标下的实验结果对比

    (a) Amazon数据集. 在该数据集上，本文提出的算法在5个指标上占优.
    F1↑ Accuracy↑ Precision↑ MAE↓ Recall↑ RMSE↓
    NTRFC 0.912 6±0.002 9(1) 0.867 4±0.003 0(1) 0.966 5±0.002 1(1) 0.236 9±0.005 2(1) 0.864 5±0.003 5(10) 0.514 8±0.011 4(1)
    Cosine 0.895 1±0.001 9(2) 0.864 8±0.002 7(2) 0.915 7±0.002 2(3) 0.440 7±0.006 5(3) 0.875 5±0.002 8(6) 0.741 4±0.007 4(2)
    ED 0.877 0±0.001 2(9) 0.846 8±0.003 3(10) 0.879 4±0.003 7(8) 0.643 6±0.006 4(10) 0.874 7±0.003 2(8) 0.934 4±0.011 2(10)
    BC 0.893 1±0.002 0(4) 0.858 9±0.003 6(4) 0.916 8±0.003 1(2) 0.432 2±0.009 1(2) 0.870 6±0.003 2(9) 0.744 1±0.013 8(3)
    PCC 0.893 2±0.002 0(3) 0.862 9±0.002 3(3) 0.912 4±0.002 8(4) 0.473 9±0.007 2(4) 0.874 8±0.001 9(7) 0.782 0±0.009 3(4)
    MD 0.877 4±0.001 2(8) 0.847 6±0.002 4(9) 0.879 3±0.003 3(9) 0.640 4±0.005 8(9) 0.875 6±0.001 5(5) 0.932 5±0.010 6(9)
    Sorensen 0.879 4±0.001 3(10) 0.851 1±0.003 2(7) 0.878 2±0.003 1(10) 0.638 0±0.007 0(8) 0.880 5±0.001 6(2) 0.928 1±0.012 1(8)
    Canberra 0.880 5±0.001 1(6) 0.853 1±0.002 3(6) 0.881 9±0.003 1(6) 0.627 4±0.006 5(6) 0.879 1±0.001 6(3) 0.916 2±0.011 1(6)
    Lorentzian 0.882 2±0.000 7(5) 0.855 6±0.001 8(5) 0.882 0±0.002 9(5) 0.620 4±0.005 3(5) 0.882 4±0.001 7(1) 0.908 3±0.009 8(5)
    Divergence 0.879 3±0.001 3(7) 0.851 0±0.002 8(8) 0.880 7±0.003 3(7) 0.634 7±0.006 9(7) 0.877 9±0.001 6(4) 0.926 2±0.012 3(7)
    (b) Movielens943u数据集. 在该数据集上，本文提出的算法在4个指标上占优.
    F1↑ Accuracy↑ Precision↑ MAE↓ Recall↑ RMSE↓
    NTRFC 0.700 6±0.010 4(1) 0.662 9±0.012 4(1) 0.778 8±0.004 1(1) 0.740 6±0.007 5(3) 0.636 7±0.015 1(1) 0.956 1±0.010 9(4)
    Cosine 0.697 6±0.013 4(3) 0.659 4±0.015 9(3) 0.775 6±0.006 9(4) 0.746 1±0.011 7(4) 0.633 9±0.017 9(2) 0.948 3±0.014 1(3)
    ED 0.692 7±0.010 5(9) 0.654 1±0.012 1(9) 0.769 6±0.005 2(9) 0.768 6±0.005 7(10) 0.629 8±0.014 2(8) 0.974 8±0.007 3(10)
    BC 0.698 2±0.010 2(2) 0.659 8±0.012 3(2) 0.777 9±0.004 0(2) 0.739 5±0.005 0(1) 0.633 4±0.014 2(3) 0.941 2±0.007 1(2)
    PCC 0.696 3±0.008 1(4) 0.657 9±0.010 0(4) 0.777 1±0.003 6(3) 0.740 4±0.002 5(2) 0.630 8±0.011 3(7) 0.940 8±0.004 9(1)
    MD 0.690 1±0.007 5(10) 0.651 3±0.009 1(10) 0.770 0±0.005 0(8) 0.761 7±0.010 9(6) 0.625 3±0.009 8(10) 0.965 1±0.015 2(5)
    Sorensen 0.694 4±0.008 7(5) 0.656 2±0.009 8(5) 0.770 4±0.005 2(7) 0.766 2±0.004 4(8) 0.632 1±0.011 4(4) 0.972 1±0.005 8(9)
    Canberra 0.694 4±0.009 0(6) 0.655 9±0.010 2(6) 0.771 3±0.004 5(6) 0.762 9±0.004 8(7) 0.631 5±0.010 2(6) 0.967 3±0.006 2(7)
    Lorentzian 0.693 4±0.010 2(8) 0.654 3±0.011 9(8) 0.773 0±0.004 0(5) 0.761 3±0.004 8(5) 0.628 7±0.014 4(9) 0.965 7±0.006 4(6)
    Divergence 0.693 6±0.008 5(7) 0.655 2±0.009 4(7) 0.769 1±0.004 7(10) 0.766 5±0.005 0(9) 0.631 6±0.011 1(5) 0.972 0±0.006 4(8)
    (c) Movielens706u数据集. 在该数据集上，本文提出的算法在3个指标上占优.
    F1↑ Accuracy↑ Precision↑ MAE↓ Recall↑ RMSE↓
    NTRFC 0.620 7±0.002 1(1) 0.577 9±0.003 3(2) 0.759 9±0.002 8(1) 0.712 4±0.004 9(1) 0.524 7±0.003 1(6) 0.918 9±0.005 9(2)
    Cosine 0.616 8±0.007 3(6) 0.573 9±0.009 4(7) 0.751 8±0.002 6(4) 0.729 6±0.033 5(3) 0.523 0±0.009 8(7) 0.941 0±0.052 8(3)
    ED 0.604 0±0.001 2(8) 0.559 5±0.001 8(8) 0.744 1±0.003 3(7) 0.787 2±0.002 6(9) 0.508 3±0.001 1(8) 1.03 0±0.005 0(10)
    BC 0.619 6±0.001 7(4) 0.576 8±0.002 7(4) 0.753 0±0.003 4(3) 0.713 7±0.002 9(2) 0.526 4±0.003 1(5) 0.916 9±0.003 2(1)
    PCC 0.620 0±0.002 5(2) 0.577 2±0.003 8(3) 0.753 3±0.003 8(2) 0.753 0±0.001 9(4) 0.526 7±0.004 3(4) 0.990 6±0.004 2(5)
    MD 0.603 0±0.001 7(10) 0.558 4±0.001 9(10) 0.744 9±0.003 4(6) 0.787 4±0.002 6(10) 0.506 4±0.001 1(9) 1.030±0.005 0(9)
    Sorensen 0.619 7±0.002 3(3) 0.578 9±0.002 6(1) 0.739 1±0.004 3(10) 0.780 5±0.002 0(6) 0.533 5±0.003 8(1) 1.019±0.004 6(6)
    Canberra 0.616 4±0.001 1(7) 0.574 0±0.002 3(6) 0.741 5±0.003 1(8) 0.780 2±0.006 5(5) 0.527 4±0.001 6(3) 1.02 1±0.011 1(7)
    Lorentzian 0.603 7±0.001 4(9) 0.559 1±0.001 8(9) 0.747 3±0.003 5(5) 0.782 3±0.002 5(8) 0.506 4±0.001 8(10) 1.024±0.004 7(9)
    Divergence 0.617 6±0.002 5(5) 0.575 6±0.003 2(5) 0.740 1±0.005 0(9) 0.782 1±0.002 1(7) 0.530 0±0.004 8(2) 1.022±0.004 6(8)
    (d) Eachmovie数据集. 在该数据集上，本文提出的算法在3个指标上占优.
    F1↑ Accuracy↑ Precision↑ MAE↓ Recall↑ RMSE↓
    NTRFC 0.654 4±0.000 8(1) 0.618 5±0.000 8(1) 0.759 3±0.000 6(5) 0.785 6±0.001 7(4) 0.575 0±0.001 0(1) 1.007±0.002 5(7)
    Cosine 0.653 2±0.000 8(2) 0.616 9±0.000 9(2) 0.761 6±0.000 8(1) 0.775 8±0.000 9(1) 0.571 8±0.001 2(3) 0.979 5±.0001 3(1)
    ED 0.631 0±0.000 5(9) 0.592 6±0.000 5(9) 0.754 1±0.000 7(9) 0.808 5±0.000 9(10) 0.542 4±0.000 6(9) 1.016±0.001 4(8)
    BC 0.653 1±0.000 8(3) 0.616 9±0.001 0(3) 0.761 2±0.000 7(2) 0.776 4±0.000 9(2) 0.571 9±0.001 1(2) 0.980 4±0.001 3(2)
    PCC 0.648 8±0.010 7(4) 0.612 1±0.011 8(4) 0.760 2±0.004 1(3) 0.783 3±0.015 4(3) 0.566 0±0.013 9(4) 0.987 4±0.017 6(3)
    MD 0.630 2±0.000 5(10) 0.591 6±0.004 7(10) 0.754 3±0.000 7(8) 0.808 4±0.001 0(9) 0.541 2±0.000 6(10) 1.016±0.001 5(9)
    Sorensen 0.634 7±0.000 6(7) 0.596 2±0.000 6(7) 0.756 7±0.000 7(7) 0.800 7±0.000 9(7) 0.546 7±0.000 7(7) 1.007±0.001 4(6)
    Canberra 0.635 9±0.000 7(6) 0.597 4±0.000 7(6) 0.756 8±0.000 7(6) 0.799 4±0.000 9(6) 0.548 3±0.000 8(6) 1.006±0.001 4(5)
    Lorentzian 0.637 3±0.000 7(5) 0.599 0±0.000 7(5) 0.760 1±0.000 8(4) 0.793 4±0.000 9(5) 0.548 6±0.000 9(5) 0.997 4±0.001 3(4)
    Divergence 0.632 4±0.000 5(8) 0.593 6±0.000 4(8) 0.753 1±0.000 6(10) 0.807 7±0.000 9(8) 0.545 0±0.000 7(8) 1.017±0.001 4(10)
    注：数据用x±s表示，括号内数字为排名.
    下载: 导出CSV
  • [1] EKSTRAND M D. Collaborative Filtering Recommender Systems[J]. Foundations and Trends © in Human-Computer Interaction, 2011, 4(2): 81-173. doi: 10.1561/1100000009
    [2] ZHANG S C, LI X L, ZONG M, et al. Efficient kNN Classification with Different Numbers of Nearest Neighbors[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(5): 1774-1785. doi: 10.1109/TNNLS.2017.2673241
    [3] ZHANG S, LIU L X, CHEN Z L, et al. Probabilistic Matrix Factorization with Personalized Differential Privacy[J]. Knowledge-Based Systems, 2019, 183: 104864. doi: 10.1016/j.knosys.2019.07.035
    [4] WEI J, HE J H, CHEN K, et al. Collaborative Filtering and Deep Learning Based Recommendation System for Cold Start Items[J]. Expert Systems With Applications, 2017, 69: 29-39. doi: 10.1016/j.eswa.2016.09.040
    [5] STRANG G. The Discrete Cosine Transform[J]. SIAM Review, 1999, 41(1): 135-147. doi: 10.1137/S0036144598336745
    [6] doi: http://downloads.hindawi.com/journals/jam/2013/248084.pdf HU J Y, GAO Z W, PAN W S. Multiangle Social Network Recommendation Algorithms and Similarity Network Evaluation[J]. Journal of Applied Mathematics, 2013, 2013: 248084.
    [7] RICCI F, ROKACH L, SHAPIRA B. Introduction to Recommender Systems Handbook[M]. Springer: Recommender Systems Handbook, 2011: 1-35.
    [8] LI R Z, ZHONG W, ZHU L P. Feature Screening via Distance Correlation Learning[J]. Journal of the American Statistical Association, 2012, 107(499): 1129-1139. doi: 10.1080/01621459.2012.695654
    [9] ZHANG H R, MIN F, ZHANG Z H, et al. Efficient Collaborative Filtering Recommendations with Multi-Channel Feature Vectors[J]. International Journal of Machine Learning and Cybernetics, 2019, 10(5): 1165-1172. doi: 10.1007/s13042-018-0795-8
    [10] ZHANG H R, MIN F, SHI B. Regression-Based Three-Way Recommendation[J]. Information Sciences, 2017, 378: 444-461. doi: 10.1016/j.ins.2016.03.019
    [11] QIAN G, SURAL S, GU Y L, et al. Similarity Between Euclidean and Cosine Angle Distance for Nearest Neighbor Queries[C] // Proceedings of the 2004 ACM Symposium on Applied Computing. New York: ACM Press, 2004: 1232-1237.
    [12] PATRA B K, LAUNONEN R, OLLIKAINEN V, et al. A New Similarity Measure Using Bhattacharyya Coefficient for Collaborative Filtering in Sparse Data[J]. Knowledge-Based Systems, 2015, 82: 163-177. doi: 10.1016/j.knosys.2015.03.001
    [13] CHANG D J, DESOKY A H, MING O Y, et al. Compute Pairwise Manhattan Distance and Pearson Correlation Coefficient of Data Points with GPU[C] //2009 10th ACIS International Conference on Software Engineering, Artificial Intelligences, Networking and Parallel/Distributed Computing. Daegu, Korea (South): IEEE, 2009: 501-506.
    [14] JIA X Y, LI W W, LIU J Y, et al. Label Distribution Learning by Exploiting Label Correlations[C] // Proceedings of the 32nd AAAI Conference on Artificial Intelligence. Menlo park, CA, AAAI, 2018: 3310-3317.
    [15] GENG X, HOU P. Pre-Release Prediction of Crowd Opinion on Movies by Label Distribution Learning[C] //IJCAI'15: Proceedings of the 24th International Conference on Artificial Intelligence, 2015: 3511-3517.
    [16] doi: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.154.8446&rep=rep1&type=pdf CHA S H. Comprehensive Survey on Distance/Similarity Measures between Probability Density Functions[J]. International Journal of Mathematical Models and Methods in Applied Sciences, 2007, 1(4): 300-307.
    [17] DEZA E, DEZA M M. Distances in Geometry[M] //Dictionary of Distances. Amsterdam: Elsevier, 2006: 62-80.
    [18] COX T, COX M. Multidimensional Scaling[M]. Chapman and Hall/CRC, 2000.
    [19] WANG J, DE VRIES A P, REINDERS M J T. Unified Relevance Models for Rating Prediction in Collaborative Filtering[J]. ACM Transactions on Information Systems, 2008, 26(3): 1-42.
    [20] SARWAR B, KARYPIS G, KONSTAN J, et al. Item-Based Collaborative Filtering Recommendation Algorithms[C] //Proceedings of the Tenth International Conference on World Wide Web. New York: ACM Press, 2001: 285-295.
    [21] WILLMOTT C J, MATSUURA K. Advantages of the Mean Absolute Error (MAE)over the Root Mean Square Error (RMSE) in Assessing Average Model Performance[J]. Climate Research, 2005, 30: 79-82. doi: 10.3354/cr030079
    [22] BERGER A, GUDA S. Threshold Optimization for F Measure of Macro-Averaged Precision and Recall[J]. Pattern Recognition, 2020, 102: 107250. doi: 10.1016/j.patcog.2020.107250
  • 加载中
图( 2) 表( 6)
计量
  • 文章访问数:  1634
  • HTML全文浏览数:  1634
  • PDF下载数:  131
  • 施引文献:  0
出版历程
  • 收稿日期:  2021-05-25
  • 刊出日期:  2021-10-20

多通道特征向量的新三角距离高效推荐

    通讯作者: 张恒汝，教授; 
    作者简介: 吕亚兰，硕士研究生，主要从事推荐系统的研究
  • 西南石油大学 计算机科学学院, 成都 610500
  • 收稿日期:  2021-05-25
基金项目:  国家自然科学基金项目(61902328)；四川省科技厅应用基础研究项目(2019YJ0314)；四川省青年科技创新研究团队(2019JDTD0017)；浙江海洋大学大数据挖掘与应用省重点实验室开放课题(OBDMA202005)

摘要: 为同时提高推荐系统的准确度和效率，提出了一种多通道特征向量的新三角距离推荐算法. 首先从原始评分矩阵中提取多通道特征向量；其次结合三角距离和Jaccard系数构建新三角距离；最后将该距离用于k近邻算法以表征两个项目间的相似度. 在4个真实数据集上的实验结果表明：文中提出的算法推荐效率更高，并能保持较好的推荐准确度.

English Abstract

    全文HTML

  • 开放科学(资源服务)标志码(OSID)：

  • 推荐系统是目前解决信息过载的有效手段. 协同过滤[1]是主流的推荐算法之一，它利用历史评分数据来获取用户对项目的偏好. 协同过滤按照不同的实现方式可以分为基于k近邻[2]、基于矩阵分解[3]以及基于神经网络的协同过滤算法[4]等. k近邻利用历史评分获取k个具有相似偏好的用户或者具有相似属性的项目[2]，常用表征用户或项目相似度的距离有：Cosine[5]，PCC(pearson correlation coefficient)[6]，Jaccard[7]和CPC(constrained pearson correlation)[8]. 然而这些算法大都采用用户或者项目的全局评分来计算相似度，导致其时间复杂度较高，推荐效率低.

    本文提出了一种多通道特征向量的新三角距离推荐算法(new triangular distance recommendation algorithm for multi-channel feature vector，NTRFC). 算法的输入为从原始评分矩阵中提取的多通道特征向量(简称特征向量)，在k近邻算法中采用新三角距离，从而提高推荐效率并保持较好的推荐准确度.

    首先，从原始评分矩阵中提取得到特征向量，其通道数目为原始评分矩阵中评分等级的数目[9]，将其作为输入，可有效降低算法的复杂度. 假定评分矩阵有n个用户，m个项目，以及l个评分等级. 以原始评分矩阵为输入，计算相似度的时间复杂度为O(nm)，而以多通道特征向量为输入，计算相似度的时间复杂度是O(lm). 评分矩阵中用户数目n远远大于评分等级数目l，故O(lm)远远小于O(nm). 例如，数据集Amazon(http://snap.stanford.edu/data/web-Amazonlinks.html)和Movielens943u (https://grouplens.org/datasets/movielens/100k/)的评分等级均为1~5分，故它们的通道数目为5，即每个项目的特征向量长度为5.

    其次，利用两个项目的特征向量构建新三角距离. 该距离将三角距离和Jaccard系数结合. 这是因为在提取特征向量后，损失了用户、项目以及评分之间的关系信息，仅保留用户对项目评分的数量信息. 若仅考虑三角距离，则无法精确判断项目之间的相似度. 考虑到Jaccard系数能充分利用共同评分项目数占所有项目数的比值信息，故结合Jaccard系数，从而在一定程度上弥补了原始评分信息.

    最后，将设计的新三角距离用于k近邻算法中，以判断两个项目的相似度. 本文提出的NTRFC算法与基于其他距离的k近邻算法在4个真实数据集上进行对比实验，利用6种准确度指标和运行时间进行评价. 实验结果表明：NTRFC算法运行时间低于已有算法，并在大部分准确度指标上占优.

1.   相关工作

  • 本节介绍评分系统[10]定义和常见的几种距离，本文使用的符号见表 1.

    • 1.1.   评分系统

  • 现回顾评分系统[10]的定义，令U={u1，u2，…，un}为一个推荐系统的用户集合，令T={t1，t2，…，tm}为推荐给用户的项目集合，由此，评分函数定义为

    其中，R为一个n×m的评分矩阵；R=(rip)n×m；C表示用户评价每个项目的评分等级构成的集合，如C={1，2，3，4，5}.

    表 2给出了一个用户数为5和项目数为6的评分矩阵. 评级为1~5分，则通道数为5. 评分反映出用户对项目的喜爱程度，分值越高表示用户越喜爱该项目，0表示用户未给项目评分. rip表示用户ui给项目tp的实际评分，G(tp，tq)表示对项目tp和tq共同评分的用户集合. 例如，r12=3表示用户u1给项目t2评分为3分，G(t1，t2)={u1，u4}表示对项目t1和t2共同评分的用户是u1和u4.

    • 1.2.   已有的距离

  • k近邻算法通常计算用户或项目之间的距离来寻找用户或项目的邻居，从而预测用户对项目的评分. 表 3列出了9个常用距离度量公式，并分析它们的时间复杂度.

    表 3中，Cosine[5]，ED[11]，BC[12]，PCC[6]，MD[13]，SØrensen[14-15]，Canberra[16]，Lorentzian[17]和Divergence[18]距离的时间复杂度均为O(n)，但BC[12]距离的时间复杂度为O(l). 其中，n表示输入向量的长度，l表示评分的等级数.

2.   NTRFC

  • NTRFC首先利用原始评分矩阵提取特征向量，然后基于特征向量设计新三角距离，最后将新三角距离应用到k近邻算法中.

    • 2.1.   特征向量的提取

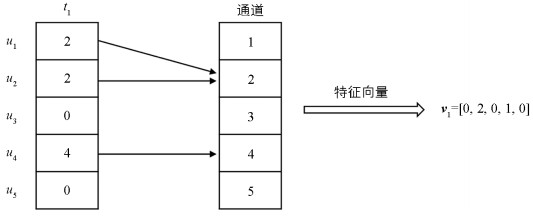
  • 项目的评分等级构成通道集合C. 例如，当评分等级为1~5分时，通道集合C={1，2，3，4，5}. 该集合包含有通道1~5，通道数l为5. 为了处理项目的离散评分，本文将每个项目的评分映射到多个通道.

    用户ui对项目tp的评分rip与通道的关系为

    其中c表示当前通道数值.

    当rip与c相等时，连接用户ui和通道c的边的数量加1. 项目tp上通道c的连接数为

    对于长度为l的通道，项目tp提取后的特征向量为

    以表 2展示的评分矩阵为例，项目t1对应的特征向量为v1= [0, 2, 0, 1 , 0]，如图 1.

    • 2.2.   新三角距离

  • 利用特征向量，设计新三角距离公式为

    其中，vp，vq分别为项目tp，tq的特征向量.NT(vp，vq)为三角距离，Jaccard(tp，tq)为Jaccard系数.

    其中‖·‖为向量的二范数. Jaccard(tp，t)为

    其中，Ip为对项目tp评过分的用户集合；Iq为对项目tq评过分的用户集合；|·|表示集合的基.

    为了更准确地描述项目之间的相似度，新三角距离引入Jaccard系数. 这是由于原始评分矩阵进行特征向量提取后，损失了用户、项目以及评分之间的对应关系信息，只保留了用户对项目评分的数量信息. 如果仅使用三角距离或其他一般距离则无法准确计算项目之间的相似度. 以表 2中项目t5和t6为例，通过提取后它们的特征向量v5和v6均为[0, 0, 0, 1 , 1] ，使用三角距离计算后相似度为1，使用Cosine距离计算后相似度也为1. 但实际上，t5和t6的评分分别来源于完全不同的用户u1，u2和u4，u5. 使用新三角距离计算得到相似度为0，更加合理.

    以表 2展示的评分矩阵为例，使用新三角距离计算项目t1和t2相似度流程如下：

    1) 提取项目t1和t2的特征向量v1=[0, 2, 0, 1 , 0]和v2= [0, 1 , 1 , 1 , 0].

    2) 计算NT距离为

    计算Jaccard系数为$\frac{{\left| {{I_1} \cap {I_2}} \right|}}{{\left| {{I_1} \cup {I_2}} \right|}} = \frac{2}{5} = 0.40$，故NTJ(v1，v2，t1，t2) =NT*Jaccard=0.29*0.4=0.116.

    • 2.3.   基于新三角距离的k近邻算法

  • 将新三角距离应用到k近邻算法[19]中，预测用户对项目的评分. 其计算公式[20]定义为

    其中，rip*表示用户ui给物品tp的预测评分；$\overline {r\left( { \bullet , {t_p}} \right)} $和$\overline {r\left( { \bullet , {t_q}} \right)} $分别为项目tp和tq的平均评分；riq为用户ui给物品tq的实际评分；Hp表示项目tp的邻居集合.

    以表 2为例，使用基于新三角距离的k近邻算法预测用户u3对t1的评分r31*流程如下：

    1) 分别提取项目t1，t3和t4的特征向量v1=[0 , 2 , 0 , 1 , 0 ]，v3= [1 , 1 , 0 , 2 , 1 ]和v4= [1 , 2 , 0 , 1 , 1 ] .

    2) 使用新三角距离分别计算项目t1和t3，t4之间的相似度NTJ(v1，v3，t1，t3)=0.11，NTJ(v1，v4，t1，t4)=0.25.

    3) 用户u3对t1的预测评分r31*=1.6+ 0.11×(4-1.6)+0.25×(5-1.6) 0.11+0.25 ≈4.69.

    • 2.4.   算法描述

  • 算法总结了NTRFC的具体步骤. 步骤1读取并初始化评分数据；步骤2根据式(2)至式(4)为每一个项目提取多通道特征向量；步骤3初始化k个邻居，并计算与邻居的新三角距离，得到最远距离D；步骤4至步骤10根据式(5)至式(7)计算与其余项目之间的新三角距离，并得到最终k个最近邻居；步骤11根据式(8)计算预测评分.

    算法  NTRFC

    输入：用户-项目评分矩阵R

    输出：预测评分rip*

    step 1：初始化评分数据

    step 2：根据式(2)至式(4)提取特征向量

    step 3：初始化k个邻居，并计算新三角距离，得到最远距离D

    step 4：for其余有评分的项目do

    step 5：根据式(5)至式(7)计算新三角距离d

    step 6：if (d＜D)

    step 7：用该项目替代最远距离项目

    step 8：D=d

    step 9：end if

    step10：end for

    step11：根据式(8)得到预测评分rip*

    算法时间复杂度分析如下：步骤1读取评分数据的时间为O(nm)；步骤2提取多通道特征向量的时间为O(nm)；步骤3初始化并计算与k个邻居的距离时间为O(kl)；步骤4至步骤10获得最近k个邻居的时间为O(ml)；步骤11预测评分的时间为O(k). 故整个模型的时间复杂度为O(nm).

3.   实验

  • 针对提出的算法进行两组对比实验，用来回答以下两个问题：1) 本文算法是否能提高推荐效率? 2) 本文提出的新三角距离能否保证较好的推荐准确度?

    问题一中采用特征向量或原始评分矩阵作为输入，使用本文提出的NTJ距离与另外9种距离计算项目间的相似度，利用k近邻算法进行协同过滤推荐，比较两者的运行时间从而判断何种输入下的推荐效率更高.

    问题二比较使用NTJ距离或其他9种距离的k近邻算法推荐准确度的高低.

    • 3.1.   数据集

  • 本文使用Amazon，Movielens943u，Movielens706u (https://grouplens.org/datasets/movielens/100k/)和Eachmovie (http://www.research.digital.com/SRC/eachmovie/)数据集. 表 4给出了它们的基本信息，前3个数据集采用的评分等级是1~5分，Eachmovie数据集采用的评分等级是0.2~1分，0分表示用户没有给项目评分. 在提取特征向量时，将Eachmovie数据集的评分等级扩展为1~5分，预测后按比例还原.

    • 3.2.   实验设计

  • 通过两组实验Exp1和Exp2分别回答本节开始提出的两个问题.

    Exp1：比较输入分别为特征向量和原始评分矩阵的算法的运行时间. 使用本文提出的NTJ距离与另外9种距离计算项目间的相似度，并将其应用于k近邻算法. 记录不同输入下，使用同样距离公式的算法在4个数据集下的运行时间，运行时间越少，表示推荐效率越高.

    Exp2：在输入为特征向量时，分别采用本文提出的NTJ距离与另外9种距离进行推荐准确度对比实验.

    在本文使用的k近邻算法中，设置两个参数LR和TR. LR表示用户是否喜欢某项目的门限值，设置为3. TR表示是否给用户推荐某项目的门限值，设置为3.5.

    采用交叉验证的方式进行实验，首先将原始评分随机分为5等份，从中选取其中4份作为训练集，1份作为测试集；其次，提取多通道特征向量，结合不同的距离预测评分；最后，通过6个指标来衡量预测评分与真实评分的差距. 上述步骤重复5次，每个指标下将得到5次不同的数据，将这些指标平均后做对比实验.

    表 5给出了6个准确度评价指标.

    • 3.3.   实验结果

    3.3.1.   Exp1的结果

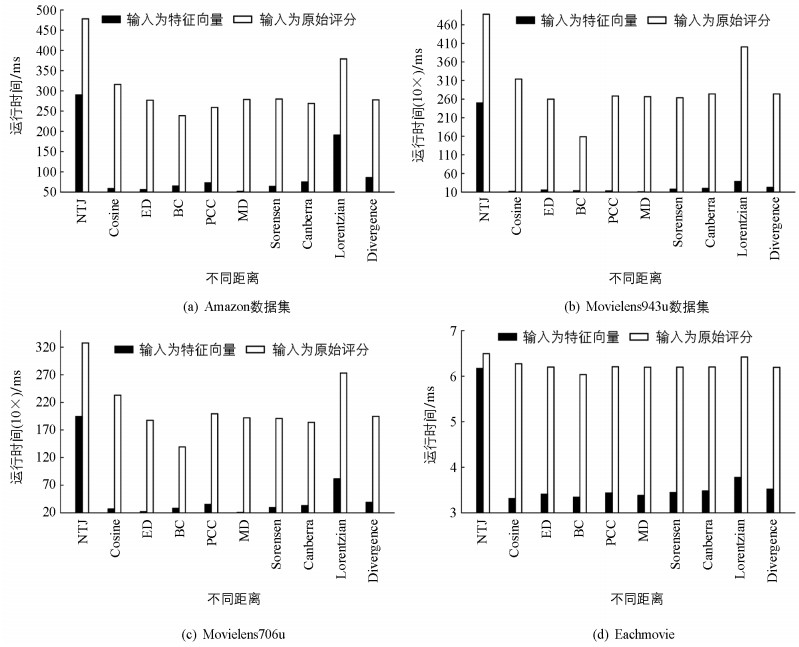
  • 在4个数据集上，分别使用特征向量和原始评分作为输入，采用本文提出的NTJ距离和其余9种已有距离计算项目相似度的k近邻算法的运行时间结果，如图 2，其中图 2(d)在Eachmovie上的运行时间进行了对数处理.

    以NTJ距离为例，对运行时间结果进行简要分析. 在Amazon数据集上，采用特征向量作为输入使得运行时间下降了39.33%，如图 2(a). 在Movielens943u数据集上，采用特征向量作为输入使得运行时间下降了48.79%，如图 2(b). 在Movielens706u数据集上，采用特征向量作为输入使得运行时间下降了40.67%，如图 2(c). 在Eachmovie数据集上，采用特征向量作为输入使得运行时间下降了52.54%，如图 2(d).

    综上所述，使用特征向量作为输入，能有效提高算法效率并大幅减少运行时间.

    • 3.3.2.   Exp2的结果

  • 不同距离在4个数据集上的准确度结果如表 6. 每一个子表包括5次实验的平均结果、标准差和平均性能排名，NTRFC为本文提出的算法，括号中的数字表示当前距离的性能排名. 若平均结果相同，则比较标准差，标准差越小，性能越好.

    在Amazon数据集上，本文提出的NTRFC算法在F1，Accuracy，Precision，MAE及RMSE评价指标上排名第一，如表 6(a)所示. 在Movielens943u数据集上，本文提出的NTRFC算法在F1，Accuracy，Precision及Recall评价指标上排名第一，如表 6(b)所示. 在Movielens706u数据集上，本文提出的NTRFC算法在F1，Precision及MAE评价指标上排名第一，如表 6(c)所示. 在Eachmovie数据集上，本文提出的NTRFC算法在F1，Accuracy及Recall评价指标上排名第一，如表 6(d)所示. 总体而言，在4个数据集上，NTRFC算法在个数准确度指标上占优.

    综上所述，本文提出的NTRFC算法能有效提高算法效率节省时间，并保持较好的推荐准确度.

4.   结论

  • 本文提出了基于多通道特征向量的新三角距离高效推荐算法. 多通道特征向量能降低算法的时间复杂度，新三角距离能更精准地描述特征向量之间的相似度. 在4个真实数据集上的实验结果表明，本文算法比已有算法在多个指标上表现得更好.

    下一步工作拟替换Jaccard系数，使用其他距离公式与三角距离结合，构建新的距离公式. 另外，考虑将新三角距离应用到可解释性推荐系统中，以期提升可解释性推荐系统的性能.

参考文献 (22)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回