-
经典的传染病仓室模型通常根据疾病痊愈后是否具有免疫阶段(即康复类仓室)分为不同研究方向[1-2],而文献[3]针对部分疫苗接种者具有暂时性免疫的实际情形,在传统无免疫阶段的SIS模型基础上加入了暂时性免疫仓室V,并引发大量研究[4-7]. 通过分析发现在疫苗接种不完全有效时,模型在一定条件下发生后向分支. 以乙型肝炎病毒为例,首先其具有垂直传染的特点;其次,可接种疫苗进行防治,但5%~10%的人群会存在疫苗无应答现象,即接种无效[8-9];同时疫苗在不同人群体内的存活时间不同[10],除新生儿外的其他易感者均可在不同阶段接种疫苗.
基于乙肝病毒的以上特点建立动力学模型,并且考虑加入由文献[11]定义的一个与病床数有关的饱和治疗函数
其中:μ0,μ1分别是最小和最大恢复率. 通过研究分析系统发生鞍结点分支、后向分支和Bogdanov-Takens分支的情况,以此推断包含病床数在内的有限医疗资源对传染病控制的影响. 此后,也有很多学者引用该治疗函数进行研究[12-15],以便更细致有效地研究与医疗资源有关的因素对传染病防治的影响.
本文基于乙肝传播特点建立一类考虑垂直传染、疫苗接种以及人均病床数量的SIVS模型,同时对易感者以及易感者和接种者的新生儿预防接种. 通过对模型进行理论研究和数值分析,总结出控制乙型肝炎疾病流的有效措施,也可进一步为进行疫苗接种的传染病防治提供了更丰富的理论基础.
全文HTML
-
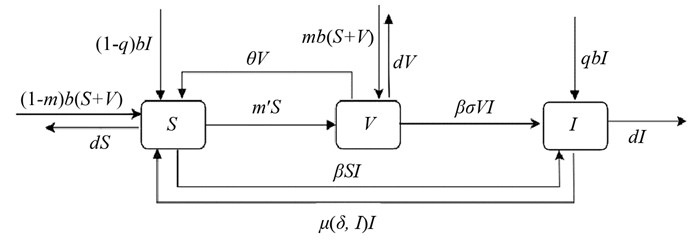
本模型将某一地区的人口共分为3个仓室:易感者、染病者以及接种者. 假设此地区不发生人口迁移和因病死亡,即环境总人口恒定,则可直接假设S(t),I(t),V(t)分别表示在t时刻环境中易感者、染病者和接种者的人口密度. 假设疾病的发生采用双线性发生率. 由于不同阶段人群染病概率不同,则设m为易感者和接种者的新生儿疫苗接种比例;m′表示易感者的接种比例;接种者与染病者接触仍有一定染病概率,这取决于疫苗的接种效率σ,σ∈(0,1),σ取0代表疫苗完全有效,取1代表疫苗完全失效;q表示疾病的垂直传染率;β表示染病者对易感者和接种者的感染率;b,d分别表示人口的出生率和自然死亡率,假设人口的出生率与自然死亡率相等,即b=d;μ为(1)式表示的治疗函数;δ为人均病床数量,可以衡量包括病床数在内的医疗资源情况;θ表示接种失效的比例. 该模型的传播流程图如下:
根据传播流程图,建立如下模型:
由于S=1-I-V,将模型进行化简降维后,模型(1)可化为:
要使模型具有实际的生物学意义,则在区域:
内考虑模型(2)的动力学性质.
-
令模型(2)的右端函数为0,可以得到该模型的无病平衡点
$\boldsymbol{E}_0=\left(0, \frac{m^{\prime}+m b}{m^{\prime}+\theta+b}\right) $ .本节将采用第二代生成矩阵法计算疾病的基本再生数R0. 那么
通过F,V在无病平衡点E0处的Jacobi矩阵得到基本再生数表达式:
注 此处R0>0恒成立. 由于模型中参数均在(0,1)范围内,则有b>(1-σ)mb.
-
模型(2)的无病平衡点
$\boldsymbol{E}_0=\left(0, \frac{m^{\prime}+m b}{m^{\prime}+\theta+b}\right) $ 始终存在. 下面着重讨论地方病平衡点的存在性.令模型(2)右端函数为0,可得
$ V(I)=\frac{\left(m b+m^{\prime}\right)(1-I)}{\beta \sigma I+m^{\prime}+\theta+b}$ ,将其代入模型中可得到I满足以下方程:其中:
由于三次方程的根较为复杂,将利用几何学的方法对其进行证明.
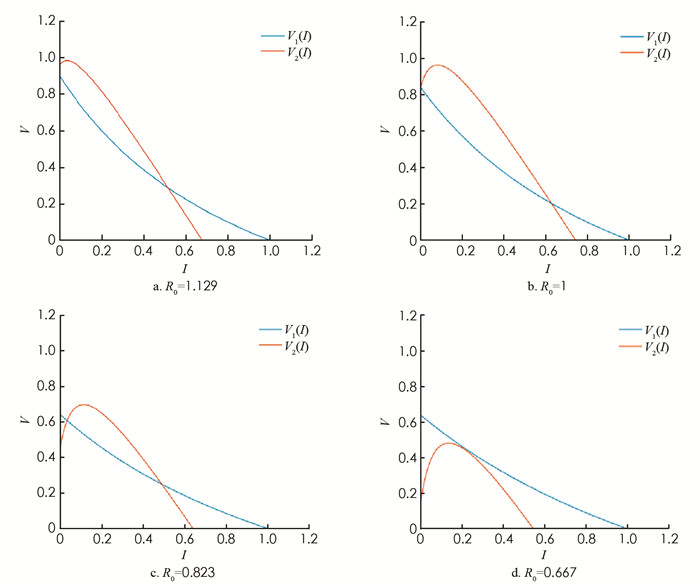
定理1 (地方病平衡点存在性) 对于模型(2)地方病平衡点E=(I,V)的存在性有以下情形:
1) 当R0>1时,模型有且仅有一个地方病平衡点
$\hat{\boldsymbol{E}}=(\hat{I}, \hat{V}) $ ;2) 当R0=1时,若
$V_1^{\prime}(0)<V_2^{\prime}(0) $ ,即此时模型有且仅有一个地方病平衡点
$ \tilde{\boldsymbol{E}}=(\tilde{I}, \tilde{V})$ ;3) 当R0 < 1时,若V′1(0) < V′2(0)且存在一点I*,使得V1(I*) < V2(I*),则模型存在两个地方病平衡点E1=(I1,V1),E2=(I2,V2);当且仅当在该点处V1(I*)=V2(I*)且V′1(I*)=V′2(I*)时两平衡点重合,仅存在一个地方病平衡点.
证 令模型(2)的右端函数为0,则有
其中
下面利用V1(I)和V2(I)的增减性及凹凸性进行分析.
由上述判断可知,V1(I)是在[0, 1]上单调递减的凹函数,V2(I)是[0, 1]上的凸函数. 又由于
则V1(0)>V2(0)等价于R0 < 1;V1(0)=V2(0)等价于R0=1;V1(0) < V2(0)等价于R0>1.
下面针对R0的3种情形(图 2)分别进行讨论:
情形1 若R0>1,有V1(0) < V2(0)且V1(1)=0,V2(1) < 0成立,则V1(I)与V2(I)在[0, 1]内有且仅有一个交点(如图 2a).
情形2 若R0=1,有V1(0)=V2(0)且V1(1)=0,V2(1) < 0成立,则当V′1(0) < V′2(0)成立时,即
$\beta\left(m^{\prime}+\theta+b\right)^2-\beta(1-\sigma)\left(m b+m^{\prime}\right) $ $\left(m^{\prime}+\theta+b\right)-\beta^2 \sigma(1-\sigma)\left(m b+m^{\prime}\right) $ <$ \frac{\left(\mu_1-\mu_0\right)\left(m^{\prime}+\theta+b\right)^2}{\delta}$ 成立时,V1(I)与V2(I)在[0, 1]内有且仅有一个交点,否则将无交点(如图 2b).情形3 若R0 < 1,有V1(0)>V2(0)且V1(1)=0,V2(1) < 0成立:
1) 当V′1(0) < V′2(0)且存在一点I*,使得V1(I*) < V2(I*),V1(I)与V2(I)在[0, 1]内存在两个交点(如图 2c);
2) 当存在一点I*使得V1(I*)=V2(I*)且V′1(I*)=V′2(I*)时,两交点重合为一个交点(如图 2d).
-
定理2(无病平衡点局部稳定性) 当R0 < 1时,模型(2)的无病平衡点E0在D内局部渐近稳定;当R0>1时,E0不稳定;当R0=1时,E0为鞍结点,其中当C>0时,E0为右鞍左结点;当C < 0时,E0为左鞍右结点.
证 模型(2)的Jacobi矩阵为:
代入无病平衡点
$\boldsymbol{E}_0=\left(0, \frac{m^{\prime}+m b}{m^{\prime}+\theta+b}\right) $ ,得到在E0点处的Jacobi矩阵为若R0-1 < 0,即R0 < 1时,J(E0)有两个负特征根,此时模型(2)在E0处局部渐近稳定;若R0-1>0,即R0>1时,J(E0)的两个特征根为异号实根,此时E0为鞍点,不稳定. 若R0-1=0,J(E0)具有一个零实部和一个负实部特征根,属于临界情形下的奇点分析. 下面利用Liapunov-Schmidt更替法进行讨论.
1) 坐标平移. 将无病平衡点E0平移至坐标原点,并作线性替换,令
$I^{\prime}=I, V^{\prime}=V-\frac{m b+m^{\prime}}{m^{\prime}+\theta+b} $ 则将模型化为2) 利用二元函数麦克劳林展式将右端函数展开,得到如下系统:
其中:
3) 判断临界情形下的奇点稳定性.
令系统(6)的第二式右端函数为0. 当|x|«1时,可利用待定系数法求解得到V′关于I′的函数. 令V′(I′)=a1I′+a2I′2+O(I′3),则
可得
则V′关于I′的函数关系为:
将V′(I′)代入系统(6)第一式中,得到降维后的系统:
其分支余维为1,它的一个普适开折拓扑等价于:
通过分析其轨线拓扑分类,可得在R0=1时,无病平衡点E0为鞍结点.
现可分析得到以下结论,令
则当C>0时,E0为右鞍左结点;当C < 0时,E0为左鞍右结点.
定理3 (地方病平衡点局部稳定性) 模型(2)地方病平衡点E =(I,V)的稳定性如下:
1) 若R0>1,模型中仅存在唯一一个地方病平衡点
$ \hat{\boldsymbol{E}}=(\hat{I}, \hat{V})$ ,且为非鞍点;2) 若R0 < 1,当满足定理2条件3时模型中存在两个地方病平衡点,其中平衡点E1=(I1,V1)为鞍点始终不稳定,平衡点E2=(I2,V2)是非鞍点.
对于所有非鞍点,在条件D>0成立时均是局部渐近稳定的.
证 模型(2)在地方病平衡点E =(I,V)处的Jacobi矩阵为:
其对应的特征方程为:
其中
同时,令D=δ[βδ(σ+1)+μ0-μ1+2(m′+θ+b)].
显然,矩阵J(E)特征根的符号由G(I)和H′(I)共同决定. 当R0>1时,由图 2a知
$ H^{\prime}(\stackrel{\Lambda}{I})>0, \stackrel{\wedge}{E}=$ $(\hat{I}, \hat{V}) $ 为非鞍点;当R0 < 1时,若满足存在两个平衡点条件,则由式(4)可知H′(I1) < 0,H′(I2)>0,此时E1=(I1,V1)为鞍点,E2=(I2,V2)为非鞍点. 对于所有的非鞍点,当D>0时是稳定的. -
定理4 在R0=1时,当条件β>βc成立,或β < βc且δ < δc成立时,模型(2)将会产生后向分支.
证 令μ1
$ =\frac{\beta\left[\theta+b+\sigma m^{\prime}-(1-\sigma) m b\right]}{m^{\prime}+\theta+b}-(1-q) b$ ,则当且仅当μ1=μ1时,有R0=1. 根据文献[16]计算决定系统零解局部动力学性质的A,B得出系统产生后向分支的条件. 现利用无病平衡点平移至原点并展开后的系统(6)进行计算.设系统(6)线性部分构成的矩阵Y在零特征根处所具有的非负左、右特征向量分别为υ,ω. 其中
求得左右特征向量分别为:
设系统(6)的右端函数各分量表示为fi(x,η)(i=1,2). 现令x1=I′,x2=V′,η=μ 1-μ1. 则右端函数展式可表示为:
其余分量二阶导结果均为0. 则
在R0=1时,若A>0,B>0,系统会产生后向分支. 由于此时B>0成立,只需
则有
从式(7)可以看出,若满足条件:
即令
则当条件β>βc时,系统可以产生后向分支.
而当β < βc时,则只需满足条件:
即当满足条件
时,系统也会产生后向分支. 令
$ \delta_c=\frac{\left(\mu_1-\mu_0\right)\left(m^{\prime}+\theta+b\right)^2}{\beta\left(\beta_c-\beta\right) \sigma(1-\sigma)\left(m b+m^{\prime}\right)} $ .综上所述,当β>βc或β < βc时,令δ < δc时,模型(2)会产生后向分支.
值得注意的是,定理2中的C>0等价于:
则在R0=1,即无病平衡点为右鞍左结点时,系统(2)会产生后向分支.
2.1. 基本再生数
2.2. 平衡点存在性
2.3. 平衡点稳定性
2.4. 后向分支
-
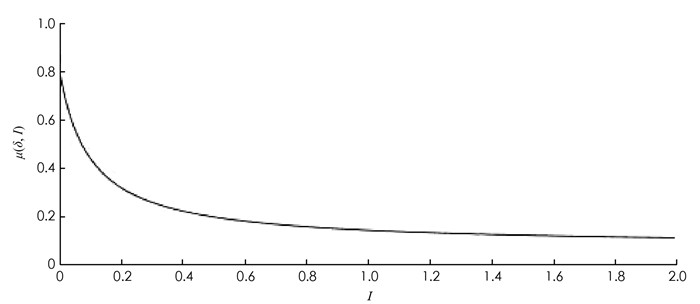
1) 固定参数μ0=0.08,μ1=0.8,δ=0.1分析了饱和治疗函数的图像(图 3). 图 3表明,对于任意的δ>0,饱和治疗函数总介于μ0与μ1之间,并且当I=δ时治疗率达到中等水平,说明包含医院人均病床数在内的医疗资源数量与治疗效果密切相关,与此同时,治疗函数μ随染病者密度I的增大而呈减小的趋势并最终趋于最小恢复率,从另一层面也表明了有限的医疗资源会限制疾病的治疗.
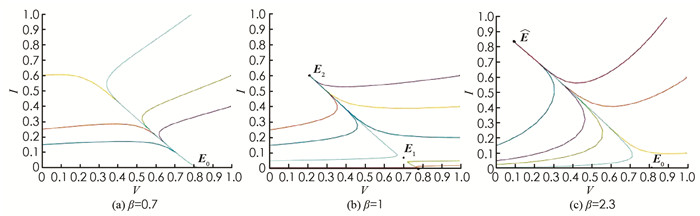
2) 固定参数μ0=0.1,μ1=0.6,θ=0.1,m′=0.4,m=0.6,σ=0.2,b=0.06,q=0.06,且令人均病床数δ=0.1不变,绘制出在β取不同值时系统(2)在相平面(V,I)内的轨迹图(图 4). 图 4表明平衡点的个数及类型会随β发生变化. 图 4(a)取参数β=0.7,系统存在唯一的无病平衡点E0且稳定;图 4(b)取参数β=1,系统存在两个正平衡点以及一个稳定的无病平衡点,其中E1为鞍点,E2为稳定的结点;图 4(c)取参数β=2.3,系统存在一个不稳定的无病平衡点和一个稳定的结点.
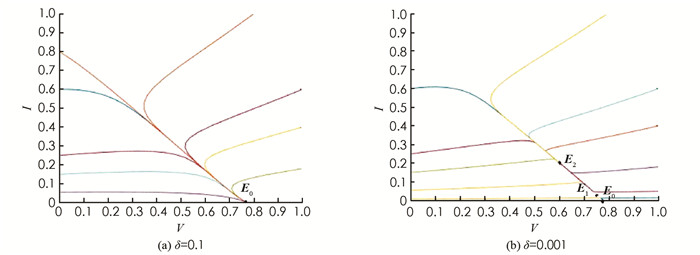
固定参数μ0=0.1,μ1=0.6,θ=0.1,m′=0.4,m=0.6,σ=0.2,b=0.06,q=0.06,令有效接触率β=0.5不变,绘制出在δ取不同值时系统(2)在相平面(V,I)内的轨迹图(图 5). 图 5表明平衡点的个数及类型会随δ发生变化. 图 5(a)取参数δ=0.1,系统存在唯一的无病平衡点E0且稳定;图 5(b)取参数δ=0.001,系统存在两个正平衡点以及一个稳定的无病平衡点,其中E1为鞍点,E2为稳定的结点.
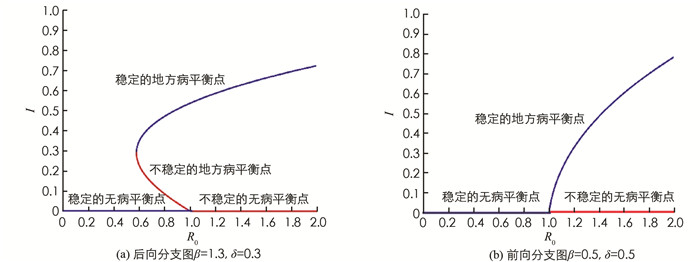
3) 固定参数σ=0.6,m′=0.4,θ=0.7,m=0.6,b=0.2,q=0.2,μ0=0.1,μ1=0.6. 图 6(a)中假设β=1.3,δ=0.3,此时模型产生后向分支,在R0 < 1时既存在局部稳定的无病平衡点,还存在两个地方病平衡点,其中不稳定的鞍点会随R0的增加最终消失,稳定的平衡点会逐渐趋于一个稳定水平. 图 6(b)中假设β=0.5,δ=0.5,此时模型发生前向分支,即R0 < 1时只存在一个稳定的无病平衡点,而R0>1时模型存在唯一一个稳定的地方病平衡点. 研究后向分支的目的就是为避免选取使模型产生后向分支的参数,以使疾病可以在R0 < 1时走向消亡.
-
根据本文得到的基本再生数式(3),相较于文献[14]得到的基本再生数:
其中d表示自然死亡率. 特殊地,当总人口恒定,即
$ \frac{\mathit{\Lambda}}{d}=1$ 时,属于文献[14]的特殊情况,此时与本文所作假设相同.对于基本再生数式(3):
1) 当q=0时,基本再生数(3)式转化为
与式(7)比较后可以看出,新生儿接种比例m与基本再生数R0(1)呈负相关,即增加对易感者和接种者新生儿的预防接种因素后,会使基本再生数减小,从而缩短疾病消失或稳定的时间.
当m=0时,基本再生数式(3)转化为:
可以看出,垂直传染率q与基本再生数R0(2)呈正相关,即增加新生儿垂直传染的传播特征后,会使基本再生数增大,从而延长疾病消失或稳定的时间.
-
平衡点的相关结论与文献[14]所得到的结果基本一致,均得到了当基本再生数大于1时系统存在一个稳定的地方病平衡点和一个不稳定的无病平衡点;当基本再生数小于1时,除稳定的无病平衡点外系统还存在一个或两个地方病平衡点,其稳定条件类似.
-
相较于文献[14]所得到的后向分支产生条件:
依据本章得到的发生后向分支的条件:
可以看出,在加入对易感者和接种者新生儿的预防接种因素后,产生后向分支的参数δ范围相对扩大,这对于控制疾病而言,参数δ在发生后向分支的范围之外选取才有显著作用.
4.1. 基本再生数
4.2. 平衡点类型
4.3. 后向分支条件
-
本文基于乙型肝炎等传染病,考虑疫苗接种存在暂时性免疫且有一定接种效率的实际情况,同时考虑到乙肝病毒可以垂直传染,建立了具有暂时性免疫仓室的一类考虑垂直传染、接种及医院病床数的SIVS传染病模型,通过理论证明和定量模拟,进一步完善具有暂时性免疫的传染病研究,并得到相关结论:
1) 当疾病的基本再生数大于1时,随时间推移疾病的染病者数量会逐渐趋于一个稳定水平;当疾病的基本再生数小于1且人均医院病床数大于一定值时,随时间推移疾病将逐渐消亡.
2) 当疾病接触率β>βc或人均医院病床数量δ < δc时,疾病会发生后向分支,此时无病平衡点在R0=1时为右鞍左结点. 这意味着在基本再生数小于1时,既存在稳定的无病平衡点也存在稳定的地方病平衡点,而控制疾病流行需要调节参数使其处于不发生后向分支的范围.
3) 通过理论研究发现,加入垂直传染的传播特点后,基本再生数会相对增大并延长疾病走向消亡的时间;而加入对易感者和接种者新生儿的预防接种措施后,可以有效缓解基本再生数的增加,控制疾病的流行,同时发生后向分支的参数δ范围也会扩大,控制疾病时应使得接触率和人均病床数处于不发生后向分支的范围内.
4) 通过以上理论证明及数值模拟的结果,可作如下解释:通过尽量减少易感者、接种者与染病者的有效接触,极大的丰富包括人均病床数在内的医疗资源,可以避免发生后向分支,从而使疾病走向消无;同时也可以通过增加对新生儿的预防接种比例和接种效率控制疾病.
在实际生活中,曾有报道乙肝患者的子代由于未接种乙肝疫苗导致多年后患病并死亡的实例,所以还可考虑对未发生垂直传播的染病者新生儿进行接种的实际情形,今后可根据这一特点继续进行研究. 同时,也可以考虑年龄结构、心理效应及媒体报道等对此类疾病的影响.



 下载:
下载: