-
本文考虑以下线性约束优化问题
其中f(x)是
$\mathbb{R}$ n1→$\mathbb{R}$ 上的非凸可微函数且g(y)是
$\mathbb{R}$ n2→$\mathbb{R}$ 上的凸可微函数,矩阵A ∈$\mathbb{R}$ m×n1,B ∈$\mathbb{R}$ m×n2. 问题(1)有着广泛的应用[1-4].当问题(1)的目标函数是凸可分时,交替方向乘子法(ADMM)是解决这类问题较为有效的方法[5-8]. 若目标函数非凸,则通过一些假设条件,ADMM仍然可以保持较好的适用性[9-14]. 其中,文献[10-11]针对非凸问题提出了Bregman ADMM并证明了其收敛性,该算法在分别求解子问题时,在原本的增广拉格朗日函数上增加了一个Bregman距离函数,通过将非凸子问题进行一个凸化处理来简化原来的子问题,进而对其进行求解. 文献[13]提出了非凸Proximal ADMM,该算法在子问题中引入了近端项,将子问题进行凸化处理,进而使用ADMM进行求解,而文献[15]在处理非凸问题上考虑的是近似二次项,近似二次项在保证问题凸化的同时还能使得迭代点不会偏离稳定点太多,这为凸化处理提供了更好的方向.
当考虑问题(1)中的有界约束时,使用ADMM直接解决是比较困难的. 幸运的是,文献[15]在处理有界多面体上的非凸优化问题时引入了梯度投影算法,对含有有界约束的单块优化问题进行了求解并取得了较好的结果. 受以上文献启发,在借鉴梯度投影和交替方向乘子法(ADMM)两种经典方法思想的基础上,本文针对具有可分结构的非凸优化问题提出了一种新的近似交替方向乘子法(P-ADMM),基于ADMM的框架在解决有界多面体上的非凸子问题时,采用梯度投影,以此简化非凸子问题的求解,降低运算成本,并且通过引入一个“平滑的”(即指数加权)原始迭代序列,并在每次迭代时,向增广拉格朗日函数中增加一个以平滑的原始迭代为中心的近似二次项,使所得到的近似增广拉格朗日函数在每次迭代时被不精确地最小化,在保证算法的收敛性的同时也能够提升算法的收敛速度. 该算法可有效应用于求解一类非凸的船舶分布式能源管理问题.
全文HTML
-
1)
$\mathbb{R}$ n1为n1维欧氏空间,$\mathbb{R}$ n2为n2维欧氏空间.2)
$\mathbb{R}$ m×n1是m×n1维实矩阵空间,$\mathbb{R}$ m×n2是m×n2维实矩阵空间.3) [·]+是约束P上的投影算子,满足
$[\boldsymbol{x}]_{+}=\operatorname{argmin}_{\bar{\boldsymbol{x}} \in P}\|\boldsymbol{x}-\bar{\boldsymbol{x}}\|$ ,特别的,[x]+的第i个坐标分量满足4) 令
${\mathit{\pmb{ω}}}=(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}, {\mathit{\pmb{λ}}}), {\mathit{\pmb{ω}}}^t=\left(\boldsymbol{x}^t, \boldsymbol{y}^t, \boldsymbol{z}^t, {\mathit{\pmb{λ}}}^t\right), \widetilde{{\mathit{\pmb{ω}}}}=(\boldsymbol{x}, \boldsymbol{y}, \tilde{\boldsymbol{y}}, \boldsymbol{z}, {\mathit{\pmb{λ}}}), \widetilde{{\mathit{\pmb{ω}}}}^t=\left(\boldsymbol{x}^t, \boldsymbol{y}^t, \boldsymbol{y}^{t-1}, \boldsymbol{z}^t, {\mathit{\pmb{λ}}}^t\right)$ . -
原问题(1)的KKT条件如下
其中:λ*,μ*,ν*,λ*为乘子;μi*和νi*表示第i个分量. 令X*×Y*为满足KKT条件的所有(x*,y*)所构成的集合,称X*×Y*为原问题(1)的稳定解集,并令W={(x,y,λ)|(x,y),λ为一对原始对偶解}.
-
(Ⅰ)
$\boldsymbol{B B}^{\mathrm{T}} \succcurlyeq \mu_0 \boldsymbol{I}$ ,其中μ0>0,即B是列满秩的.(Ⅱ) f(x)是可微的,且满足Lipschitz可微条件
则可得,存在γ < 0,使得
(Ⅲ) g(y)是强凸的,强凸系数为m,即
(Ⅳ) g(y)是可微的,且满足Lipschitz可微条件
(Ⅴ) 存在常数
$\tilde{\sigma}>0$ ,使得(Ⅵ) 函数g(y)是强制的,即
-
接下来介绍近似的交替方向乘子法(P-ADMM),问题(1)的增广拉格朗日函数为
其中常数α>0. 经典的ADMM算法处理以下两个子问题:对于固定的y,λ,在有界约束P上极小化L(x,y,λ);对于固定的x,λ,极小化L(x,y,λ). 最后,利用原始残差Ax + By = b更新乘子λ. 由于有界约束的特殊性,在求解有界非凸子问题上采用梯度投影,且考虑到f(x)是非凸的,通过引入一个指数平均(或平滑)方案来生成一个额外的序列{zt},并在增广的拉格朗日函数中插入一个额外的以zt为中心的二次近似项,在保证非凸子问题凸化的同时也能够使得原始迭代点xt不会偏离稳定迭代点太多.
注1 该算法与传统的ADMM相比的优势在于,传统的ADMM处理有界约束上的非凸子问题是十分困难的,一方面是子问题的非凸性,另一方面则是有界约束的限制,而采用梯度投影、引入近似二次项则可以简化子问题的求解,很好地处理了非凸性和有界约束,使得算法更加简便,降低了运算成本.
注2 与文献[15]算法相比,P-ADMM是投影算法和ADMM的结合,主要用于解决有界约束上的可分离的非凸优化问题,而文献[15]中的算法主要用于解决有界约束上的单块非凸优化模型,是本文模型的一种特殊情况,因此P-ADMM的应用性更加广泛.
注3 与文献[16]中算法APGMM相比,P-ADMM在解决有界约束上的非凸子问题时不是直接采用的梯度投影,而是在原本的增广拉格朗日函数上引入了近似二次项,近似二次项的引入在保证非凸子问题凸化的同时也加快了算法收敛的速度(见数值实验).
1.1. 论文的符号定义
1.2. 稳定解集合
1.3. 基本假设
1.4. 一种近似的ADMM
-
为了更加方便分析P-ADMM的收敛性,首先给出一些关键的引理.
引理1 若假设(Ⅰ),(Ⅳ)成立,那么可得
证 首先,通过假设(Ⅰ)可得
利用算法关于y在t+1步迭代式的一阶最优性条件可得
再通过算法关于λ在t+1步的迭代式可得
$\nabla g$ (yt+1)=-〈 B,λt+1〉,同理可得通过假设(Ⅳ)可知,函数g(x)是梯度Lipschitz连续的,则
结合(2),(3)式可得
$\left\|\boldsymbol{\lambda}^{t+1}-\boldsymbol{\lambda}^t\right\|^2 \leqslant \frac{L_2^2}{\mu_0}\left\|\boldsymbol{y}^{t+1}-\boldsymbol{y}^t\right\|^2$ ,故引理1成立.引理2 若假设(Ⅱ)成立,且p+γ>0,令函数
则下列结论成立:
1) 函数K(x,y,z,λ)关于x是强凸的,且强凸系数为γk=p+γ,即
2) 函数K(x,y,z,λ)关于x是梯度Lipschitz连续的,且Lipschitz系数为Lk=p+γ+ασ12,即
其中σ1为矩阵A的最大奇异值.
证 对函数K(x,y,z,λ)关于x求梯度,则
由假设(Ⅱ)知
同理可得
则引理2成立.
接下来,构造辅助函数
其中η>0,证明函数列
$ M\left(\widetilde{\boldsymbol{\omega}}^t\right)$ 的单调递减性和有界性.引理3 若假设(Ⅰ),(Ⅲ)和(Ⅳ)成立,
$\widetilde{\boldsymbol{\omega}}^t=\left(\boldsymbol{x}^t, \boldsymbol{y}^t, \boldsymbol{y}^{t-1}, \boldsymbol{z}^t, \boldsymbol{\lambda}^t\right)$ 为P-ADMM所生成的点列,那么对任意的t,若$2 c<\frac{1}{L_k}, \alpha>\max \left\{\frac{2 L_2^2}{\mu_0(m-2 \eta)}, \frac{1}{\mu_0 \tilde{\sigma}}\right\}>0$ ,有注4 当矩阵B为对称矩阵,即BT= B,且满足
$2 c<\frac{1}{L_k}, \alpha>\max \left\{\eta+\sqrt{\frac{2 L_2^2}{\mu_0}+\eta^2}, \frac{1}{\mu_0 \tilde{\sigma}}\right\}>0$ 时,将假设(Ⅲ)中函数g(y)的强凸性弱化成凸性,仍然能够保证辅助函数列$M\left(\widetilde{\boldsymbol{\omega}}^t\right)$ 的单调递减性.证 由算法关于x在t+1步的迭代式及投影定理,可得
则有
通过引理2的结论1),利用函数K(x,y,z,λ)关于x的凸性,有
结合(4),(5)式和引理2的结论2)以及
$2 c<\frac{1}{L_k}$ ,可得通过算法关于z在t+1步的迭代式得到
由假设(Ⅲ)可知
利用算法关于y在t+1步迭代式的一阶最优性条件得
再利用算法关于λ在t+2步的迭代式可得
结合(8),(9)式可得
最后,通过算法关于λ在t+1步的迭代式可得
再由引理1可得
将(6),(7),(10),(11)式相加,则有
故引理3成立.
引理4 若假设(Ⅰ)和(Ⅳ)成立,
$\widetilde{\boldsymbol{\omega}}^t=\left(\boldsymbol{x}^t, \boldsymbol{y}^t, \boldsymbol{y}^{t-1}, \boldsymbol{z}^t, \boldsymbol{\lambda}^t\right)$ ,序列$\left\{\widetilde{\boldsymbol{\omega}}^t\right\}$ 由P-ADMM产生,若α>$\max \left\{\frac{2 L_2^2}{\mu_0(m-2 \eta)}, \frac{1}{\mu_0 \tilde{\sigma}}\right\}>0$ ,那么$\left\{\widetilde{\boldsymbol{\omega}}^t\right\}$ 是有界的,且函数列$\left\{M\left(\widetilde{\boldsymbol{\omega}}^t\right)\right\}$ 有下界.证 首先,通过完全平方可得
再利用假设(Ⅰ)和(Ⅳ),可得
因此
将(13)式代入(12)式可得
由引理3可知,函数列
$M\left(\widetilde{\boldsymbol{\omega}}^t\right)$ 是单调递减的,则有由于函数f(x)是有界闭集P上的可微函数,则函数f(x)是有界的,由于
$\alpha>\max \left\{\frac{2 L_2^2}{\mu_0(m-2 \eta)}, \frac{1}{\mu_0 \tilde{\sigma}}\right\}>0$ ,结合(14),(15)式可知,序列$\left\{\boldsymbol{x}^t\right\}, \left\{\left\|\nabla g\left(\boldsymbol{y}^t\right)\right\|\right\} \text { 和 }\left\{\left\|\boldsymbol{y}^t-\boldsymbol{y}^{t-1}\right\|\right\}$ 都是有界的,通过(13)式进一步可知函数列{λt}也是有界的. 由假设(Ⅵ)可知$\inf\limits_{\boldsymbol{y}} g(\boldsymbol{y})>-\infty$ ,则序列{yt}是有界的. 因此,序列$\widetilde{\boldsymbol{\omega}}^t$ 是有界的. 由假设(Ⅵ)和(14)式有$M\left(\widetilde{\boldsymbol{\omega}}^t\right)>-\infty$ . 综上所述,序列$\left\{M\left(\widetilde{\boldsymbol{\omega}}^t\right)\right\}$ 是有下界的.将P-ADMM的迭代点
$\boldsymbol{x}^t, \boldsymbol{y}^t, \boldsymbol{z}^t, \boldsymbol{\lambda}^t$ 记为$\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}, \hat{\boldsymbol{z}}, \hat{\boldsymbol{\lambda}}$ ,并将算法中x,y,z,λ的更新变量定义为$\hat{\boldsymbol{x}}^{+}, \hat{\boldsymbol{y}}^{+}, \hat{\boldsymbol{y}}^{+}, \hat{\boldsymbol{\lambda}}^{+}$ ,则下面的引理说明,若算法停止,则可以找到一对原始对偶解.
引理5 若
那么
$(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}, \hat{\boldsymbol{\lambda}}) \in W$ 是原问题的一对解.证 由(16)式以及
$(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}, \hat{\boldsymbol{z}}, \hat{\boldsymbol{\lambda}})=\left(\hat{\boldsymbol{x}}^{+}, \hat{\boldsymbol{y}}^{+}, \hat{\boldsymbol{z}}^{+}, \hat{\boldsymbol{\lambda}}^{+}\right)$ ,可得到以下等式进一步简化得到
由于
$\hat{\boldsymbol{x}} \in P$ ,则有如下等式成立则
$(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}, \hat{\boldsymbol{\lambda}})$ 满足原问题(1)的KKT条件,即有$(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}, \hat{\boldsymbol{\lambda}})$ ∈W为原问题的一对解.推论1 若假设(Ⅰ),(Ⅲ)和(Ⅳ)成立,对于任意ε>0,存在δ(ε)>0,且
$(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}, \hat{\boldsymbol{z}}, \hat{\boldsymbol{\lambda}}), \left(\hat{\boldsymbol{x}}^{+}, \hat{\boldsymbol{y}}^{+}, \left.\hat{\boldsymbol{z}}^{+}, \hat{\boldsymbol{\lambda}}^{+}\right)\right.$ 为P-ADMM产生的相邻两个迭代点,满足我们可得
证 反证,假设存在序列
$\left\{\hat{\boldsymbol{x}}^k\right\}, \left\{\hat{\boldsymbol{y}}^k\right\}, \left\{\hat{\boldsymbol{z}}^k\right\}, \left\{\hat{\boldsymbol{\lambda}}^k\right\}$ 满足对于某个ε0>0和任意的δ>0,当成立时,即
则有
通过引理4可知,由算法P-ADMM产生的迭代序列是有界的,则存在子列
$\left\{\hat{\boldsymbol{x}}^{k_i}\right\}, \left\{\hat{\boldsymbol{y}}^{k_i}\right\}, \left\{\hat{\boldsymbol{z}}^{k_i}\right\}, \left\{\hat{\boldsymbol{\lambda}}^{k_i}\right\}$ 满足进而可以得到
则有
由引理5可得
$(\overline{\boldsymbol{x}}, \overline{\boldsymbol{y}}, \bar{\boldsymbol{\lambda}}) \in W$ ,即则有
通过(17)式可得
则有
这与(18)式矛盾,则推论1成立.
定理1 若假设(Ⅰ),(Ⅲ)和(Ⅳ)成立,序列{ ωt}为P-ADMM所产生,则下列结论成立
1)
$\lim\limits_{t \rightarrow \infty}\left(\left\|\boldsymbol{x}^t-\boldsymbol{x}^{t+1}\right\|+\left\|\boldsymbol{y}^t-\boldsymbol{y}^{t+1}\right\|+\left\|\boldsymbol{z}^t-\boldsymbol{z}^{t+1}\right\|+\left\|\boldsymbol{\lambda}^t-\boldsymbol{\lambda}^{t+1}\right\|\right)=0$ 2)
$\lim\limits_{t \rightarrow \infty}\left\|x^{t+1}-z^t\right\|=0$ 3)
$\lim\limits_{t \rightarrow \infty} \operatorname{dist}\left(z^t, X^*\right)=0, \lim\limits_{t \rightarrow \infty} \operatorname{dist}\left(\left(\boldsymbol{x}^t, \boldsymbol{y}^t\right), X^* \times Y^*\right)=0, \lim\limits_{t \rightarrow \infty} \operatorname{dist}\left(\left(\boldsymbol{x}^t, \boldsymbol{y}^t, \boldsymbol{\lambda}^t\right), W\right)=0$ 证 1)由引理3可知
由引理4知函数列
$\left\{M\left(\boldsymbol{\omega}^t\right)\right\}$ 有下界,则极数$\sum_{t=1}^{\infty} M\left(\boldsymbol{x}^t, \boldsymbol{y}^t, \boldsymbol{y}^{t-1}, \boldsymbol{z}^t, \boldsymbol{\lambda}^t\right)-M\left(\boldsymbol{x}^{t+1}, \boldsymbol{y}^{t+1}, \boldsymbol{y}^t, \boldsymbol{z}^{t+1}, \boldsymbol{\lambda}^{t+1}\right)$ 是收敛的,因此进而可得到
通过定理1可知
则可得
结论1)成立.
2) 由于
结合z的第t+1次迭代式zt+1= zt+β(xt+1- zt)可得
则结论2)成立.
3) 由1),2)两个结论可得
结合推论1有
则结论3)成立.
-
本文考虑用P-ADMM解决一类非凸的船舶分布式能源管理问题,在文献[17]中,考虑具有多个代理的船舶动力系统,且各代理根据各自的需求、供给相互协调. 首先将船舶能量管理问题以多智能体系统的形式重新制定,然后利用交替方向乘子法(ADMM)寻找模型中满足共识要求的最经济的工作点,本文考虑如下可分非凸光滑的能量成本函数
其中
F(x)为能量成本函数,xi为共识变量,D为该问题的维度,问题(19)可等价转化成如下问题
问题(20)所对应的增广拉格朗日函数为
利用P-ADMM求解问题(20).
本文实验在配置英特尔Core i5-6200U 2.30 GHz处理器、4.00 GB内存和Windows 10(64位)操作系统的计算机上进行,其中t为迭代步数. 算法的参数设置如下:p=8 000,
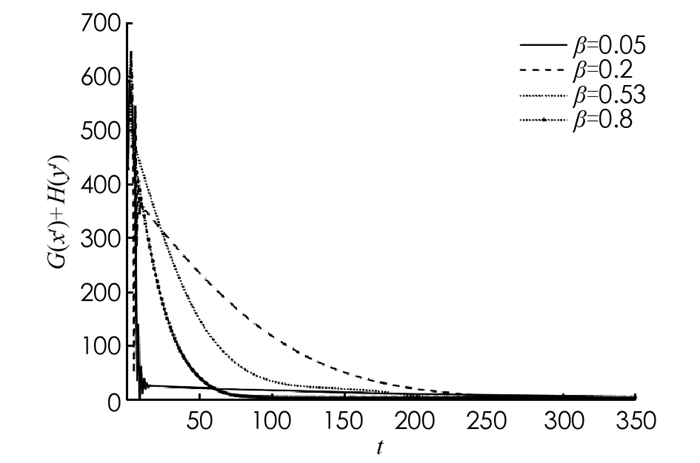
$c=\frac{1}{5000}$ ,D=50,α=100,y0,z0,λ0都是维数50的零向量,x0∈$\mathbb{R}$ 50为均匀分布在[-5.12,5.12]上的向量,终止条件图 1展示了在P-ADMM算法下船舶电力系统能量成本的走势情况,其中G(xt)+H(yt)为成本函数,t为迭代步. 通过图 1可以看出,能量成本值从开始的下降逐渐趋于稳定,最后达到收敛. 同时,观察发现选择较大的β,会使收敛速度加快,即算法可以在更小的迭代步数下完成收敛,减少了算法迭代的次数.
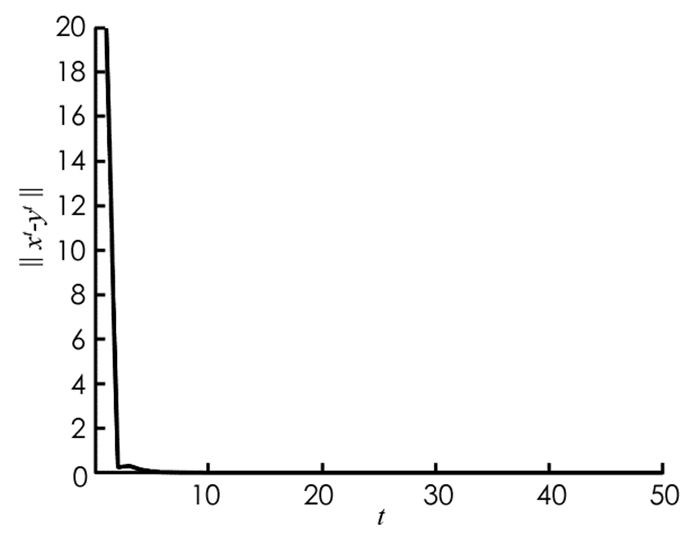
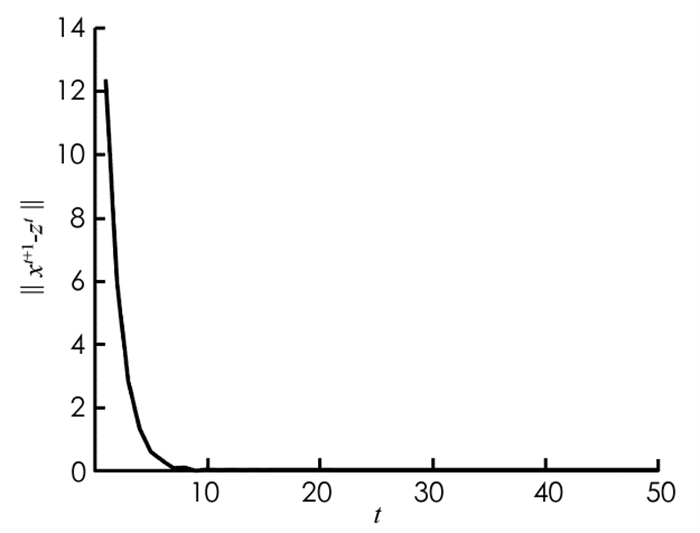
图 2和图 3分别展示了在参数β=0.2的条件下‖ xt- yt‖和‖ xt+1- zt‖的下降情况,进一步验证了算法P-ADMM解决问题(20)的可行性. 从图 2,3中可知,‖ xt- yt‖和‖ xt+1- zt‖一开始下降得非常快,再逐渐趋于平稳并达到收敛.
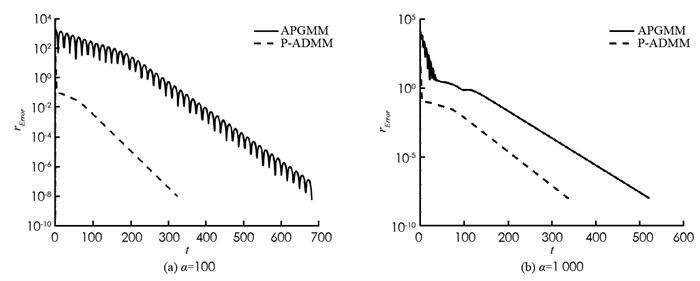
图 4是基于问题(20)将P-ADMM和APGMM[17]在参数β=0.8的条件下进行了比较. 从图 4中可以看到算法P-ADMM相对于算法APGMM在下降趋势和收敛步数上都具有较大的优势. APGMM算法开始迭代是波动的、不稳定的. 考虑到目标函数的非凸性,我们在运行算法时,选取α=100,α=1 000两种情况进行比较. 由图 4可知算法P-ADMM的下降速度快,能够在更小的迭代步达到收敛.
-
本文在梯度投影算法和ADMM基础上,针对可分结构的非凸优化问题,提出了一种新的P-ADMM,该算法具有良好的收敛性,简化了子问题的求解,降低了运算成本,且近似二次项的引入在保证算法的收敛性的同时也能够提升算法的收敛速度. 该算法在一类非凸的船舶能源管理问题中也得到了有效应用. P-ADMM在梯度投影时,选取的步长是满足条件的定值,但如何优化梯度投影的步长以提高算法速率需要进一步的研究.



 下载:
下载: