以近7届(第26~32届)夏季奥运会男子100 m成绩数据为研究对象，数据来源于中国奥运会官方网站，数据可靠.

通过中国知网查阅近20年相关文献资料50余篇为本研究提供一定的理论基础.

运用Matlab7.5统计软件对收集的数据进行处理分析.

在灰色理论中通常把X⁽⁰⁾(k)+az⁽¹⁾(k)=b称作灰色模型GM(1，1)的定义型，记为GM(1，1，D). 模型释义^[9]：①GM(1，1)灰色模型是灰色预测的基础，它是由一个包含单变量的一阶微分方程构成的模型，即含义为1阶(Order)，1个变量(Variable)的灰(Grey)模型. ②灰色模型中a的大小以及符号反映X⁽⁰⁾(及X⁽¹⁾)的发展态势，称a为灰色模型中的发展系数. ③b为灰色模型中的灰作用量，其内涵为系统的作用量，但是它不可以直接观测，可通过计算得到，是等效的作用量，是具有灰信息覆盖的作用量，故称作灰作用量. ④z⁽¹⁾(k)的序列：z⁽¹⁾=(z⁽¹⁾(2)，z⁽¹⁾(3)，…z⁽¹⁾(n))；z⁽¹⁾(k)=0.5x⁽¹⁾(k)+0.5x⁽¹⁾(k-1)，称为白化背景值序列；基于每个白化背景值z⁽¹⁾(k)都是x⁽¹⁾(k)与x⁽¹⁾(k-1)的平均值，故记z⁽¹⁾为MEAN x⁽¹⁾，即z⁽¹⁾=MEANx⁽¹⁾.

设时间序列X⁽⁰⁾有n个观测值，X⁽⁰⁾={x⁽⁰⁾(1)，x⁽⁰⁾(2)，x⁽⁰⁾(3)，…，x⁽⁰⁾(n)}，通过累加生成新序列X⁽¹⁾，X⁽¹⁾={x⁽¹⁾(1)，x⁽¹⁾(2)，x⁽¹⁾(3)，…，x⁽¹⁾(n)}，则GM(1，1)灰色模型相应的微分方程为$ \frac{d x^{(1)}}{d t}+a X(1)=b$. 式中，a为发展系数，b为灰色作用量. 设α为待估参数向$ \alpha=\left(\frac{a}{b}\right)$，利用最小二乘法可得^[9]：α=(B^TB)^-1B^TY_n，其中，$\boldsymbol{B}=\left[\begin{array}{cc} -\frac{1}{2}\left[X^{(1)}(1)+X^{(1)}(2)\right] & 1 \\ -\frac{1}{2}\left[X^{(1)}(2)+X^{(1)}(3)\right] & 1 \\ \cdots & \cdots \\ -\frac{1}{2}\left[X^{(1)}(n-1)+X^{(1)}(n)\right] & 1 \end{array}\right] $，B^T为B的转置矩阵，(B^TB)^-1为(B^TB)矩阵的逆矩阵，$ Y_n=\left[\begin{array}{c} X^{(0)}(2) \\ X^{(0)}(3) \\ \cdots \\ X^{(0)}(n) \end{array}\right]$，求解微分方程，可得GM(1，1)灰色模型的时间相应序列：$\stackrel{\wedge}{X}(k+1)=\left(x^{(0)}(1)-\frac{b}{a}\right) e^{-a k}+\frac{b}{a}, k=0, 1, 2, \cdots, n $.

本研究对近7届(第26~32届)夏季奥运会100 m冠军数据(表 1)尝试建立GM(1，1)灰色预测模型，通过统计软件计算所得到的新的时间序列称为生成列.

累加生成序列

则$ \boldsymbol{B}=\left[\begin{array}{lr} -\frac{1}{2}\left[X^{(1)}(1)+X^{(1)}(2)\right] & 1 \\ -\frac{1}{2}\left[X^{(1)}(2)+X^{(1)}(3)\right] & 1 \\ -\frac{1}{2}\left[X^{(2)}(1)+X^{(1)}(3)\right] & 1 \\ -\frac{1}{2}\left[X^{(3)}(1)+X^{(1)}(4)\right] & 1 \\ -\frac{1}{2}\left[X^{(1)}(5)+X^{(1)}(6)\right] & 1 \\ -\frac{1}{2}\left[X^{(1)}(6)+X^{(1)}(7)\right] & 1 \end{array}\right]=\left[\begin{array}{ll} -14.95 & 1 \\ -24.89 & 1 \\ -34.79 & 1 \\ -44.645 & 1 \\ -54.505 & 1 \\ -64.275 & 1 \end{array}\right] ; Y_n=\left[\begin{array}{l} 9.87 \\ 9.85 \\ 9.69 \\ 9.63 \\ 9.81 \\ 9.80 \end{array}\right]$

$ \left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}} Y_n=\left[\begin{array}{r} 0.0042 \\ 10.0214 \end{array}\right]$，即a=0.004 2；b=10.021 4

所以，GM(1，1)灰色模型的白化方程为$ \frac{d x^{(1)}}{d t}+0.0042 X(1)=10.0214$，X⁽⁰⁾(1)=9.84，$\frac{b}{a} $=2 386.047 6，时间响应式$ \stackrel{\wedge}{X}(k+1)=\left(x^{(0)}(1)-\frac{b}{a}\right) e^{-a k}+\frac{b}{a}$，即$\hat{X}(k+1)=-2376.0576 e^{-0.0042 k}+ 2 386.047 6$，即得出的预测模型为$\hat{y}=-2376.0576 e^{-0.0042 k}+2386.0476 $.

预测一般是指对未来事件的可能性和不确定性进行分析与总结叙述. 对于竞技体育成绩的预测与分析来说，其预测的精度和可靠性是至关重要的^[10]，所以还应对所建模型的相关指标进行检验以确保预测模型的精确度以及竞技体育成绩的有效性^[11].

将k=0，1，2，3，4，5，6分别代入构建的预测模型中可得序列：

累减生成$\hat{X}^{(0)} $序列：$ \hat{X}^{(0)}$=[9.990 9，9.959 4，9.936 8，9.855 2，9.833 8，9.792 6，9.751 6]

绝对误差序列：△⁽⁰⁾=[0.000 9，0.039 4，0.023 2，0.015 2，0.036 2，0.057 4，0.061 6]

相对误差序列：φ=[0.009 0%，0.397 1%，0.232 9%，0.154 4%，0.366 7%，0.582 7%，0.635 7%]

相对误差均小于0.65%，模型精确度较高.

$\eta(i)=\frac{\min \left\{\varDelta_i^{(0)}\right\}+\rho \max \left\{\varDelta_i^{(0)}\right\}}{\varDelta_i^{(0)}+\rho \max \left\{\varDelta_i^{(0)}\right\}}, i=1, 2, 3 \cdots, n $，ρ=0.5. 式中，ρ为分辨率，0 < ρ < 1，一般取ρ=0.5，当ρ=0.5时，关联度大于0.6，预测模型即为满意^[11].

本例中，min{Δ_i⁽⁰⁾}[0.000 9，0.039 4，0.023 2，0.015 2，0.036 2，0.057 4，0.061 6]= 0.000 9，max{Δ_i⁽⁰⁾}=[0.000 9，0.039 4，0.023 2，0.015 2，0.036 2，0.057 4，0.061 6]= 0.061 6，关联系数：η(k)=[1，0.451 56，0.587 03，0.689 13，0.773 13，0.359 41，0.343 07].

关联度计算公式$ \gamma=\frac{1}{n} \sum_{i=1}^n \eta(k)$，本例中关联度结果为r=$\frac{1}{7} $(1+0.451 56+0.587 03+0.689 13+0.773 13+0.359 41+0.343 07)=0.600 47. 满足关联度r＞0.6的检验准则.

利用SPSS17.0统计软件计算出原始序列的标准差S₁=0.098 80，绝对误差序列的标准差S₂=0.022 09. 根据方差比公式$C=\frac{S_2}{S_1} $可以计算出C值，为0.223 58；小误差概率计算公式P=p{|Δ⁽⁰⁾(i)- Δ⁽⁰⁾|＜0.674 5 S₁}，令e_i=|Δ⁽⁰⁾(i)-Δ⁽⁰⁾|，S₀=0.674 5 S₁，则小误差概率S₀=0.674 5×0.098 80=0.066 64，e_i=[0.033 28，0.010 98，0.030 246，0.018 98，0.002 02，0.023 22，0.027 42]，可以看到，所有的e_i值都小于S₀，故P=1，C＜0.35. GM(1，1)灰色模型精度级别分级标准见表 2.

经过残差检验、关联度检验和后验差检验后，结果表明该模型均达到了模型检测的统计参考标准，具有良好的精度和一定的实用价值，可以用模型$\hat{y}=-2376.0576 e^{-0.0042 k}+2386.0476 $对第33届奥运会男子100 m金牌成绩进行预测，还原值为y=2 376.057 6 e^{-0.004 2k}(e^{0.004 2}-1)，当k=7时，y=9.700 7 s，即第33届夏季奥运会男子100 m金牌的预测成绩为9.700 7 s.

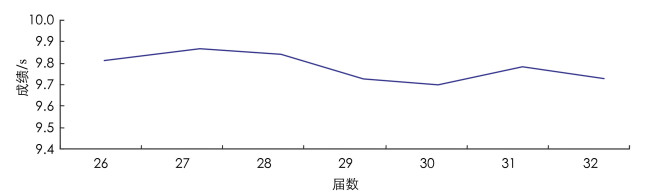
在竞技体育比赛中，运动员的成绩是现场比赛的水平体现，是运动员竞技能力最直接最有效的反映，更是对运动员训练成效的检验与客观评定^[12]. 本研究以近7届奥运会男子100 m金牌比赛成绩为原始数据，绘制金牌成绩变化折线图. 从图 1可知，第26~32届奥运会男子100 m的金牌成绩曲线呈波浪式摆动，随时间序列的动态变化呈一定的变化趋势. 整体上来看，第26~32届奥运会男子100 m金牌成绩呈小周期性逐步提高. 据该走向分析，第33届夏季奥运会男子100 m金牌成绩很有可能呈现“回冷期”，也就是说第33届奥运会男子100 m金牌成绩要比伦敦奥运会上牙买加选手博尔特创造的9.63 s还稍差一些. 当然这是一场理论上的预测，仅能说明本研究奥运会100 m金牌成绩的预测结果在某种程度上遵循了竞技成绩变化发展的一般规律. 运动员的成绩变化与走向在理论研究上能较精确地加以预测分析，但随着训练技术的突破和训练器材与科技装备的日益发展，在某个时期或阶段运动员的成绩有可能成爆发式的增长与突破. 比如在北京奥运会上，美国游泳运动员菲尔普斯由于最新科技的比赛装备再结合自身优异的竞技水平，在该奥运会上共荣获7枚金牌，打破了多项世界记录创造了多项历史. 理论上预测分析竞技运动员成绩变化与走向，是一种常规化状态下的考量与分析，并不包括特殊情况，这也是以后体育学者进行研究探讨时需要综合考虑的. 奥运会运动成绩的变化与走向是各国体育科研工作者长期跟踪与关注的重点，能否精确地预测和分析成绩的变化与发展趋势，对各教练员、运动员目标战略的实施有着重要的参考意义，所以通过奥运项目的成绩尤其是金牌成绩的准确预测与分析对未来该项目的发展至关重要.

每一届奥运会成绩深受人们的关注，尤其是100 m金牌成绩，对其成绩的预测和分析也是该项目工作者的重点研究方向之一. 在进行竞技体育成绩预测时，要根据项目的属性进行定性与定量的多方面考虑，不能仅仅为了预测而预测^[13]. 众所周知，运动员的竞技成绩尤其是奥运会成绩，受到很多因素的影响，比如运动员个人的竞技能力、赛事心理状态、赛事环境以及裁判的裁定水平等. 在对成绩进行预测时，灰色模型理论中对这些因素及其相互关系要求并不高，在进行理论建模时只要把这些能影响成绩的综合因素作为在一定时间与范围内的有关灰色量，用这些数据列建立预测模型即可^[14]. 需要说明的是灰色系统理论研究的是已知或未知部分信息，运动员成绩的影响因素并非确定的，在进行数据建模时可将它们视为一个灰色系统. 本研究结合实际情况，对夏季奥运会男子100 m金牌成绩(为减少计算误差，取小数点后4位)进行了灰色理论的GM(1，1)模型预测. 从表 3可知，夏季奥运会的预测精度中，第32届100 m成绩的预测精度位列第一，达到99.9%；第29届奥运会成绩的预测精度最弱，为99.3%，与前几届成绩的精度相比，起伏相对较大. 第29届奥运会100 m决赛由于牙买加选手博尔特的超常发挥，大大影响了统计学的预测效果. 这也说明了当某个项目有重大技术突破或超级天赋运动员出现时，统计预测学会存在相对较大的误差. 当然这只是研究事件的偶然性与特殊性，并不代表研究的常态化情况. 从本研究预测与分析精度的整体上来看，第26~32届奥运会男子100 m的平均预测精度为99.6%，说明预测模型具有足够的精度，具有一定的预测应用价值.

在解读GM(1，1)灰色模型的定义、模型的构建等基础上，建立了奥运会男子100 m金牌成绩GM(1，1)灰色预测模型，并对模型进行了残差检验、后验差检验，模型精度均为一级. 模型关联度大于0.6，精度高，为奥运会男子100 m金牌成绩的预测与发展规律提供了积极的理论参考.

运用GM(1，1)灰色预测模型对第26~32届夏季奥运会的成绩进行了预测，预测精度平均为99.6%，说明模型有较高的精度，具有一定的实用价值. 对第33届奥运会男子100 m成绩进行预测，结果为9.700 7 s.