-
开放科学(资源服务)标识码(OSID):

-
灾害种类多、发生频率高、分布地域广、受灾损失重是我国的基本国情之一[1]。随着我国城市群建设的快速推进,重特大安全风险呈逐年增加趋势。在重特大安全风险转化为灾害过程中,除灾害本身直接造成损失外,缺乏有效、恰当的应对策略也是造成损失的重要原因[2],例如:应急物资调度因层级间和层级内协作缺乏优化而应急响应效率低下,灾害管理社会目标因应急资源分配不公而难以实现等。应急物资在突发事件应对中极其重要,我国政府高度重视应急物资储备保障工作,目前已经形成了中央、省、市、县、乡镇5级政府应急物资储备体系。然而,“新冠”疫情表明,应急物资储备不足、调配效率偏低、储备库网络协同水平不佳仍是应急物资保障的突出问题。2014年,京津冀协同发展作为重大国家战略被提上日程, 完善各项安全监管措施,健全各种应急救援手段,构建城市应急物资储备库网络,成为京津冀城市群综合竞争力提升和发展的重要保障。
全文HTML
-
城市群应急物资储备库网络是由城市群内应急物资储备库以及应急物资调配通道共同构成的网络状结构,常常表现出等级性特征。表 1描述了一个3等级的城市群应急物资储备库网络。
城市群应急物资储备库网络等级优化问题本质上属于设施选址问题中的等级设施选址问题。设施选址问题是有关一系列设施(如基础设施、交通站点等)如何做出合理位置选择的问题[3]。等级设施选址问题是设施选址问题研究中极具复杂性、挑战性,且与现实联系密切的一个领域[4-5],对于公共设施网络优化有重要指导意义[6-8]。学者们从等级设施网络优化中的单流与多流模式划分[9]、服务可用性考察中的嵌套和非嵌套特征[10]、空间优化中的同调性和非同调性结构[11],以及整体优化中的单目标与多目标实现[12]等维度展开了研究。陈志宗[13]探索了城市防灾减灾设施的等级网络优化问题;杨珺等[14]构建了碳排放政策影响的多容量等级设施选址模型;陆相林等[15]基于等级设施选址模型,对北京房山应急物资储备库网络优化问题进行了实证研究;常征等[16]对内陆港等级选址问题展开研究;Yavari等[17]提出了考虑不确定性、覆盖半径扩展和容量受限的重构型等级设施选址问题,并设计启发式算法求解;Chouksey等[18]基于印度产妇保健设施可获得性有限的困境,从用户和政府角度规划所需的产妇保健设施,构建了容量受限的等级设施选址配置模型,并设计了序贯算法加以求解;霍非舟等[19]构建了考虑需求等级与距离损失的消防站选址模型。
在应急物资储备库优化模型方面,项寅[20]构建了社会环境以及需求特征限制型应急物资储备模型;胡建华等[21]、罗振敏等[22]综述了我国应急物资储备研究主要领域及趋势;常征等[23]基于引力模型原理改进最大覆盖模型,构建了多目标海上应急物资储备库等级选址模型,设计了蝙蝠算法进行求解。
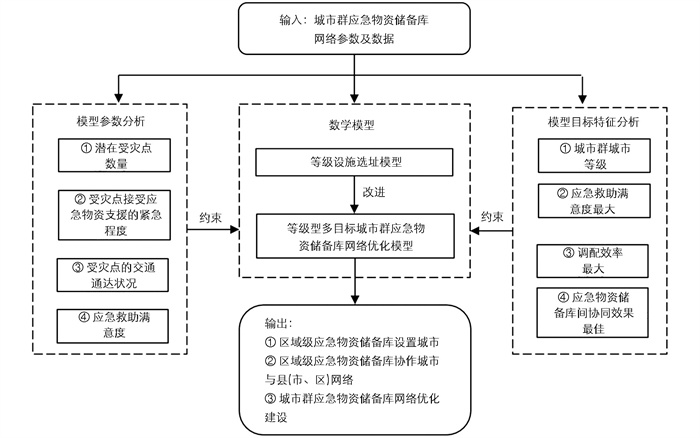
等级设施选址和应急物资储备库优化模型相关研究已经取得了丰硕成果,但是对应急物资储备库网络中的等级多目标优化问题缺乏充分关注,实证中鲜有定量探讨城市群应急物资储备库网络等级配置合理性的成果。基于上述考虑,本研究构建了综合体现城市群纵向“府际合作”等级性、实现城市群内受灾点民众接受应急物资配置总满意度最大、使得应急物资储备库之间总关联度最高和应急物资储备库建设与储存成本最小的应急物资储备库网络等级型多目标优化模型,并以京津冀城市群为例进行实证,具体研究思路如图 1所示。
-
网络由节点和线组成。城市群应急物资储备库网络作为网络设施中的一种类型,其节点通常划分为2种类型。其中,接受应急物资服务的点定义为应急物资需求点,又称为潜在受灾点;具有应急物资储存以及供给功能的点,定义为应急物资储备库。对于等级型应急物资储备库网络而言,进一步考虑了应急物资储备库的等级性(亦称为层级性,或者多水平性等)特征。城市群应急物资储备库网络中的线,可以表现为实际的交通线,也可根据优化需要抽象为欧氏距离、交通时间等,本质体现了城市群应急物资储备库网络中各点之间的供需联系。
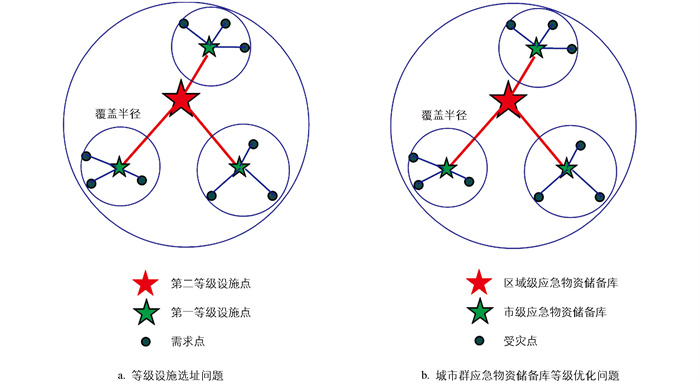
城市群应急物资储备库网络本质上等同于设施选址问题中的设施点与需求点所形成的等级网络,图 2显示了等级设施选址问题与城市群应急物资储备库网络等级优化问题的相似之处。由图 2可知,城市群应急物资储备库网络等级优化问题本质上等同于等级设施选址问题。因此可以初步判断,选用等级设施选址模型解决城市群应急物资储备库网络等级优化问题是合适的。
-
本研究的假设如下:①依据文献[15]的方法,假设城市群应急物资储备库、潜在受灾点在网络优化分析中表现为点状特征,交通线(运输线)在网络中表现为线状特征,其中潜在受灾点的实体形态设定为县(市、区),应急物资储备库的实体形态设定为地市级以及京津2个直辖市。②依据文献[16]的方法,假设将城市群应急物资储备库设定为高低2个等级,低级应急物资储备库标号为第一等级(在实证中对应市级应急物资储备库);高级应急物资储备库标号为第二等级(在实证中对应区域级应急物资储备库);把潜在受灾点标号为第0等级。③依据文献[15、19]的方法,用交通距离远近体现应急物资储备库与潜在受灾点的空间联系密切程度。④基于成本节约原理,城市群应急物资储备库数量不能无限制增加,故假设城市群应急物资储备库总数量有限。⑤依据文献[15]的方法,假设1个潜在受灾点最多接受1个应急物资储备库的应急物资调拨服务即能满足其需求;限定城市群应急物资储备库选址位于各地级市以及京津2个直辖市市域内,其功能包括:应急物资储存、调拨以及响应区域级乃至国家级城市群应急物资储备库的指示与指导。⑥考虑到城市群内城市、县(市、区)人口众多,需要建设多个应急物资储备库才能够满足应急物资需求,故假设城市群应急物资储备库在多个城市内分布,以保证其应急物资调拨服务可用性的空间均衡性。⑦依据文献[15]的方法,假设城市群潜在受灾点接受应急救助满意度遵循距离(时间)衰减规律,即接受应急救助距离越远(所需救助时间越长),其满意度越低。⑧依据文献[16, 19]的方法,假设城市群高等级应急物资储备库具有嵌套性特征,除了具备低级应急物资储备库服务可用性之外,还具备其他应急服务救助功能。
-
为了方便分析,本研究进行如下符号的定义。
-
i表示城市群潜在受灾点,I表示全部城市群潜在受灾点,故存在i∈I;j表示低级城市群应急物资储备库(即第一等级应急物资储备库,也即实证中的市级应急物资储备库),J表示低级城市群应急物资储备库的全体,故存在j∈J;k表示高级城市群应急物资储备库(即第二等级应急物资储备库,也即实证中的区域级应急物资储备库),K表示高级城市群应急物资储备库的全体,故存在k∈K。
-
pl表示低级城市群应急物资储备库的建设总量;ph表示高级城市群应急物资储备库的建设总量;VAi表示城市群潜在受灾点i的受灾人口数量;mj表示第j个城市下辖的县(市、区)个数;Rij表示潜在受灾点i至低级城市群应急物资储备库j的交通距离;Rjk表示低级城市群应急物资储备库j至高级应急物资储备库k的交通距离;Rijk表示城市群潜在受灾点i至低级应急物资储备库j,然后再至高级应急物资储备库k的总交通距离;Ei表示受灾点i接受应急物资支援的紧急程度,取值范围设定为[0, 1],越接于1,需要得到应急物资支援的紧急程度越高,反之则越低;Cjk表示k等级应急物资储备库j的建设成本;Qjk表示k等级应急物资储备库j的应急物资储备量;fjk表示k等级应急物资储备库j的单位存储成本。
Gi表示受灾点i交通通达状况的参数,取值范围设定为[0, 1];ci表示受灾点i的平均拥堵延时指数。Gi的计算公式如下:
SDij表示潜在受灾点i由低等级应急物资储备库j服务时的需求满意度,用下式计算:
SDjk表示高级应急物资储备库k调拨应急物资至低级应急物资储备库j时的应急救助满意度,用下式计算:
SDijk表示高级应急物资储备库k调拨应急物资至其责任区内的低级应急物资储备库j并使潜在受灾点i的居民获得的应急救助满意度,用下式计算:
TCjk表示k级应急物资储备库中第j个储备库的对外关联指数,用下式计算:
式中:G为引力常数;Zj、Zk为应急物资储备库保障能力,其评价指标体系及计算方法参见文献[24]。
-
xijk表示潜在受灾点变量,当潜在受灾点i被高级应急物资储备库k职责范围内的低级应急物资储备库j提供应急物资调拨服务时,令其值为1,反之取值为0;yjk表示城市群应急物资储备库指派变量,当低级应急物资储备库j接受高级应急物资储备库k应急物资调拨时,令其值为1,反之取值为0;wj表示低级城市群应急物资储备库选址变量,低级应急物资储备库选址于j点时,令其值为1,反之取值为0;zk表示高级城市群应急物资储备库选址变量,高级应急物资储备库选址于k点时,令其值为1,反之取值为0。
-
在文献[24]的目标函数基础上,进一步考虑了受灾人口、受灾点接受应急物资支援的紧急程度、受灾点交通通达状况对灾民应急救助整体满意度最大化的影响,得目标函数f1:
上述目标函数中,式(6)用于最大化评价潜在受灾点居民接受应急物资调拨所获得的整体满意度f1;式(7)用于实现应急物资储备库建设和存储成本f2的最小化;式(8)用于最优化城市群各应急物资储备库之间,以及城市群各应急物资储备库至潜在受灾点的空间联系f3。
-
约束条件仍选用文献[24]模型中的约束条件,具体如下:
约束条件中,式(9)实现了任何1个潜在受灾点最多仅可由1个应急物资储备库提供应急物资调拨服务;式(10)表示潜在受灾点只有接受某低级城市群各应急物资储备库应急物资调拨时,才取值为1,否则取值为0;式(11)、式(12)用于限定低级城市群各应急物资储备库j只有接受其高级应急物资储备库k应急物资调拨指派时,才能取值为1,否则取值为0;式(13)表示低级应急物资储备库j最多只能接受1个高级应急物资储备库k的应急物资调拨指派;式(14)、式(15)依次限定了低级、高级城市群各应急物资储备库的预定建设数量;式(16)实现了高级城市群各应急物资储备库对其职责内低级城市群各应急物资储备库指派关系的同调性;式(17)保证了xijk,wj,zk,yjk取值为0或1。
2.1. 方法选取的适用性分析
2.2. 模型假设
2.3. 符号定义
2.3.1. 模型集合符号
2.3.2. 模型参数符号
2.3.3. 模型决策变量符号
2.4. 模型构建
2.4.1. 目标函数
2.4.2. 约束条件
-
等级型城市群应急物资储备库网络模型优化问题属于分层整数规划的范畴,其求解类属于NP-hard问题[26-27],只能通过启发式算法(近似算法等)来完成近似求解。本研究的启发式算法设计分为3个阶段,包括总目标函数加权求解阶段、分目标函数求解优化阶段和分目标函数值迭代阶段。
-
此阶段完成对等级型城市群应急物资储备库网络模型总目标函数的加权求解。参考文献[28]的方法,赋予目标函数f1、f2、f3权重,对三者的值进行加权处理,即有目标函数总值
$f=\sum\limits_{i=1}^3 \varphi_i \boldsymbol{\cdot} f_i$ ,其中φi是第i个目标函数值的权重。由于目标函数f1、f2、f3有不同计量单位,故对原始数据进行归一化处理。其中f1、f3为正目标,处理公式为:$x_{i j}^{\prime}=\frac{x_{i j}^{\prime \prime}-x_{\min }^{\prime \prime}(j)}{x_{\max }^{\prime \prime}(j)-x_{\min }^{\prime \prime}(j)}$ ;f2为负向目标,处理公式为:x′ij=$\frac{x_{\text {max }}^{\prime \prime}(j)-x_{i j}^{\prime \prime}}{x_{\max }^{\prime \prime}(j)-x_{\text {min }}^{\prime \prime}(j)}$ 。式中:x′ij是无量纲化后的新数据;x″ij是原始数据;x″min(j)为第j个评价指标所有取值中的最小值;x″max(j)为第j个评价指标所有取值中的最大值。 -
本阶段基于Berman等[29]提出的有关分层整数规划的求解思路,利用目标函数公式计算f1、f2、f3的值并选定应急物资储备库,具体步骤如下:
步骤1 模型参数初始化设置。
对VAi、Ei、Gi、Cjk、fjk、Qjk赋初值,并利用极差标准化对数据进行归一化处理;根据所测得的受灾点至应急物资储备库距离矩阵,求得SDijk值。
步骤2 各分目标函数值优化求解。
① 对于目标函数值f1,通过以下过程求解:对任一潜在受灾点i,计算其接受各应急物资储备库应急物资调拨服务时所有可能的VAi·Ei·Gi·SDijk取值,并由大到小降序排列。选取其最大值对应的应急物资储备库(设为j),验证是否满足模型约束条件,如果满足则赋值xijk=1,否则选取VAi·Ei·Gi·SDijk值排序中位列第2的应急物资储备库(设为j′)。同样验证是否满足约束条件,如果满足则赋值xij′k=1,否则选取VAi·Ei·Gi·SDijk值排序中位列第3的应急物资储备库,依次完成类似操作直至目标函数值f1在满足模型约束条件下达到最优。②对于目标函数值f2,通过以下过程求解:对任一应急物资储备库j,计算其所有可能的(Cjk+fjk·Qjk)取值,并由小到大升序排列。选取其最小值对应的应急物资储备库(设为j),验证是否满足模型约束条件,如果满足则赋值yj′k=1,否则选取(Cjk+fjk·Qjk)值排序中位列第2小的应急物资储备库(设为j′)。同样验证是否满足约束条件,如果满足则赋值yj′k=1,否则选取(Cjk+fjk·Qjk)值排序中位列第3小的应急物资储备库,依次完成类似操作直至目标函数值f2在满足模型约束条件下达到最优。③对于目标函数值f3,通过以下过程求解:对任一应急物资储备库j,计算其所有可能的TCjk取值,并由大到小降序排列。选取其最大值对应的应急物资储备库(设为j),验证是否满足模型约束条件,如果满足则赋值yjk=1,否则选取TCjk值排序中位列第2的应急物资储备库(设为j′)。同样验证是否满足约束条件,如果满足则赋值yj′k=1,否则依次完成类似操作直至目标函数值f3在满足模型约束条件下达到最优。
步骤3 重复执行步骤2,直至所有的城市群潜在受灾点和应急物资储备库都完成选定。需要说明的是,本阶段的计算结果是总目标函数加权求解阶段求解的基础。
-
考虑到模拟退火算法具有参数少、鲁棒性强、适用于求解复杂整数规划问题的优点,因此本阶段选择模拟退火算法作为核心算法对目标函数f1、f2、f3的取值进行迭代优化,确定城市群应急物资储备库选址点集合P。模拟退火算法基本步骤如下[24, 30-31]:
步骤1 在候选新建应急物资储备库点中随机选择p个新建应急物资储备库点,构成集合P,利用Vogel配置算法,配置各潜在受灾点,计算目标函数值F(P),作为当前最优解。设置初始点温度T=T0,初始迭代次数为0。
步骤2 在P中随机选一应急物资储备库点j,j∈P,同时在集合P选择一应急物资储备库点
$j^{\prime}, j^{\prime} \notin P$ ,移出j并移入j′,构成集合定义为P′。步骤3 通过前面设计的配置启发式算法,计算目标函数F(P′)的值。
步骤4 当F(P′)≥F(P)时,使P=P′,接受本次移动(move),转至步骤6。
步骤5 当F(P′)<F(P)时,计算δ=(F(P)-F(P′))/T,若有δ≥e-δ,则接受移动,令P=P′,转向步骤6;如不接受移动,则保持原有P,转向步骤7。
步骤6 把当前解代入F(P′),如有必要,更新最优解。
步骤7 逐一增加迭代次数,用T乘以f。如果迭代次数超过L,迭代终止,以最优解作为算法的解,否则返回步骤2。
整个算法求解过程取n≤300,T0=0.1,
$N=250 n \sqrt{p}$ ,f=1-5/N。需要说明的是,本阶段的计算结果是分目标函数求解优化阶段运算求解的基础。通过启发式算法3个阶段的联合操作,即可得到城市群应急物资储备库等级优化后的xijk和yjk值,明确城市群应急物资储备库应急物资调拨服务范围内的潜在受灾点与服务半径,也即得到了等级型城市群应急物资储备库网络的优化结果。需要说明的是,传统单目标等级设施选址优化问题只需考虑整数规划特征和等级特征即可完成启发式算法设计,故采用两阶段启发式算法(两阶段分别对应整数规划特征和等级特征)即可求解,如文献[29]即采用了两阶段启发式算法,文献[25]利用MATLAB的YALMIP工具箱进行求解。由于本研究属于等级多目标设施选址优化问题,需要在传统两阶段算法基础上进一步考虑模型的多目标特征(即需要增加一个阶段),故设计了三阶段启发式算法(三阶段分别对应整数规划特征、等级特征和多目标特征)进行求解。
3.1. 总目标函数加权求解阶段
3.2. 分目标函数求解优化阶段
3.3. 分目标函数值迭代阶段
-
本研究选择京津冀城市群为例进行实证,该城市群由北京市、天津市2个直辖市和河北省的11个地级市所构成,总面积约占全国的2.3%。受快速城市化进程以及地缘相接的特殊地理环境影响,京津冀一直面临地震、极端天气、大气污染、消防等各种突发事件威胁,且各类突发事件具有整体连锁效应。2016年至今京津冀三地相继签署了《北京市天津市河北省应急救援协作框架协议》《京津冀救灾物资协同保障联席会议制度(试行)》《京津冀救灾物资协同应急保障预案》《京津冀毗邻地区救灾和物资保障互助合作指南》等重要合作文件,旨在有效整合京津冀三地应急资源,进一步提高协同处置自然灾害和事故灾难能力,提出建立三地救灾物资协同保障组织运行机制,为京津冀协同发展保驾护航。当前,京津冀城市群尚无应急物资储备库网络的整体协同规划,由“重文件”合作到“重落实”构建高效的应急物资储备库网络仍有很长的路要走。因此,选取京津冀为实证区域,探索在京津冀城市群内建立若干应急物资协作区,统筹优化城市群内应急物资储备,实现城市群内区域级、市级应急物资高效低费用联动调配具有重要现实意义。
-
通过收集京津冀三地统计部门的数据得到2021年度13个城市常住人口、各类灾害损失情况、发生频率等信息,从而确定各城市可能受灾人口数量;查询13个城市建安成本作为应急物资储备库单位建设成本;通过高德地图网站的测距功能得到京津冀城市群13个城市两两之间的交通距离;受灾点的平均拥堵延时指数由高德地图城市交通中的城市详情查询得到,然后计算得到受灾点交通通达状况指数;利用式(5)计算得到应急物资储备库的对外关联指数。如前所述,京津冀城市群应急物资储备库划分为区域级应急物资储备库和市级应急物资储备库2类。其中,区域级应急物资储备库是城市群应急物资储备库网络的核心节点,其数量要有所限定以提高建设效率,依据优化模型多次测算和专家咨询意见确定为6个。
-
利用MATLAB R2014a软件编写三阶段启发式算法程序,运行求得优化结果(表 2)。
由表 2第1列可知,京津冀城市群6个区域级应急物资储备库的选址点分别为:北京市、天津市、石家庄市、邯郸市、张家口市、承德市,即此6个城市应当成为京津冀城市群应急物资储备库网络整体优化的关键节点,是实现京津冀城市群内潜在受灾点民众接受应急物资配置总满意度最大、应急物资储备库之间总关联度最高和应急物资储备建设与储存成本最小的关键节点。
由表 2第2列可知,与6个区域级应急物资储备库形成协作的市级应急物资储备库分别为:北京市的协作城市为廊坊市、沧州市;天津市的协作城市为唐山市、秦皇岛市;石家庄市的协作城市为保定市、衡水市;邯郸市的协作城市为邢台市;而张家口市和承德市则作为独立区域级应急物资储备库服务自身所在区域。
由表 2第3列可知,京津冀城市群各城市下辖县(市、区)的应急物资储备库优化配置情况为:①北京市作为区域级应急物资储备库所在地,为廊坊市、沧州市提供高等级应急物资调配服务,与2市形成“京廊沧”应急物资调配协作区;而且,北京市除了服务于廊坊市、沧州市外,也服务于其自身下辖16个县(市、区),最大服务半径为96 km,对应县(市、区)为延庆区。②天津市作为区域级应急物资储备库所在地,为唐山市、秦皇岛市提供高等级应急物资调配服务,与2市形成“津唐秦”应急物资调配协作区;而且,天津市除了服务于唐山市、秦皇岛市外,也服务于其自身下辖16个县(市、区),最大服务半径为120 km,对应县(市、区)为蓟州区。③石家庄市作为区域级应急物资储备库所在地,为保定市、衡水市提供高等级应急物资调配服务,与2市形成“石保衡”应急物资调配协作区;而且,石家庄市除了服务于保定市、衡水市外,也服务于其自身下辖22个县(市、区),最大服务半径为84 km,对应县(市、区)为深泽县。④邯郸市作为区域级应急物资储备库所在地,为邢台市提供高等级应急物资调配服务,二者形成“邯邢”应急物资调配协作区;而且,邯郸市除了服务于邢台市外,也服务于其自身下辖18个县(市、区),最大服务半径为105 km,对应县(市、区)为涉县。⑤张家口市作为独立区域级应急物资储备库服务自身所辖县(市、区),最大服务半径为156 km,对应县(市、区)为沽源县。⑥承德市作为独立区域级应急物资储备库服务自身所辖县(市、区),最大服务半径为171 km,对应县(市、区)为丰宁满族自治县。
-
将模型中2021年度的实证数据,替换为2019年度和2020年度的数据,得到优化结果如表 3所示。
由表 3对比可知,替换为其他年度数据后,2020年度中秦皇岛市取代承德市成为区域级应急物资储备库选址点,被取代的承德市成为天津市的协作城市,其他城市及优化结果无变化;2019年度的模型优化结果均未产生变化,故模型健性较强。
-
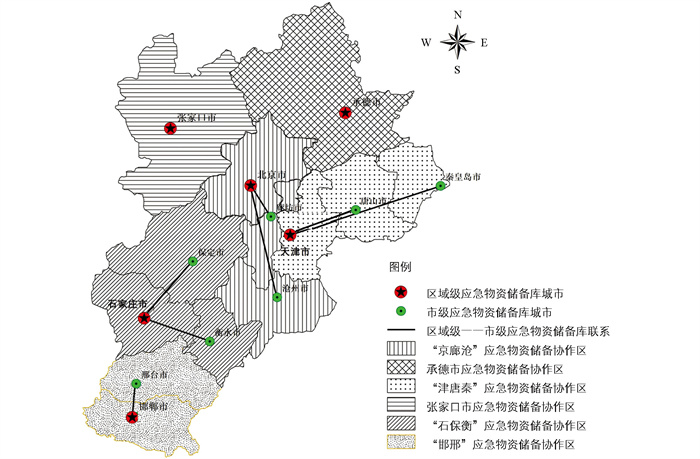
为了更为直观地体现优化结果,利用ArcGIS 10.2软件绘制京津冀城市群应急物资储备库网络等级优化示意图(图 3)。由图 3可知,本研究所构建的优化模型可以较好地实现京津冀城市群应急物资储备库网络的空间结构优化,形成了以北京市、天津市、石家庄市、邯郸市、张家口市、承德市为区域级应急物资储备库,以唐山市、保定市、廊坊市、衡水市、秦皇岛市、邢台市、沧州市为市级应急物资储备库,以京津冀城市群所有县(市、区)为外围的6大应急物资调配协作区。该结构可以实现京津冀城市群整体应急物资调配满意度的最大化、建设与存储成本的最小化和空间联系的最大化,保证京津冀城市群应急物资储备库调配网络的高效运行。
-
① 成立京津冀城市群应急物资储备库网络统一管理协调机构,要明确北京市、天津市、石家庄市、邯郸市、张家口市、承德市作为区域级应急物资储备库的核心地位,以6个区域级应急物资储备库为核心节点,构建分等级、多中心协同发展网络。②以“京廊沧”“津唐秦”“石保衡”“邯邢”合作为重点,实现区域级应急物资储备库协作区内部的密切联合。③以应急物资调配互动、共享为抓手,优化区域级应急物资储备库—市级应急物资储备库—受灾点的链接(如交通线路),进一步强化京津冀城市群应急物资储备库网络等级优化的效果。
4.1. 研究区域概况
4.2. 数据收集与区域级应急物资储备库数量确定
4.3. 优化结果
4.4. 模型稳健性检验
4.5. 京津冀城市群应急物资储备库网络等级优化示意图与优化建议
4.5.1. 等级优化示意图
4.5.2. 等级优化建议
-
由区域级、市级、县(市、区)级应急物资储备库组成,具有等级性特征的城市群应急物资储备库网络体系,对于实现城市群应急物资调配的良性互动,以及城市群公共安全与协同发展具有重要现实意义。本研究立足于解决城市群应急物资储备库网络优化问题,基于等级设施选址理论,以受灾点民众接受应急物资配置总满意度最大、应急物资储备库之间总关联度最高和应急物资储备建设与储存成本最小为目标,对传统的等级设施选址模型加以改进,构建了适用于城市群应急物资储备库网络优化的等级型设施选址模型,设计了三阶段启发式算法加以求解,并以京津冀城市群为例进行实证,确定了京津冀城市群内6个区域级应急物资储备库的选址点,优化了由区域级、市级、县(市、区)级3个等级构成的应急物资储备库网络结构,绘制了优化示意图,提出了协同发展的对策建议。
本研究只考虑了静态特征下的城市群应急物资储备库网络等级优化问题,今后可以考虑应急物资存在动态需求、应急物资储备库建设与运营受时间的动态影响、受灾点与应急物资储备库之间联系表现为不确定性、应急物资储备库库容量限制等复杂情景的等级设施选址问题,并且可以用于验证本研究模型实证结果的合理性。同时,相较于传统的NP-hard问题,本研究所构建模型的求解过程更为复杂,今后还可以探索更优的启发式算法。



 下载:
下载: