-
预应力撑杆钢柱是通过在细长受压钢柱中引入撑杆和预应力索,来提高其稳定承载能力的钢结构构件.对拉索施加预应力后,撑杆会对中心柱形成侧向支撑,从而减小中心柱的计算长度,以提升其稳定性能[1].由于稳定性好、造型美观、用料节省,预应力撑杆钢柱在国内外的工程实践中得到广泛地应用.
自上世纪70年代以来,国内外学者对预应力撑杆钢柱展开了大量的研究.文献[2]对预应力撑杆钢柱的屈曲荷载进行了研究,分析表明,预应力撑杆钢柱在仅沿柱高布置一层撑杆的情况下,其屈曲荷载可以达到相应普通受压钢柱欧拉荷载的7倍以上.文献[3]推导了单层预应力撑杆钢柱屈曲荷载和拉索初始预张力的关系.文献[4]对沿柱高设置多层撑杆的预应力撑杆钢柱进行了研究,其研究表明,增加撑杆层数可以提升此类构件的屈曲荷载,但也使得其屈曲模态更加复杂.文献[5]研究了初始几何缺陷对预应力撑杆钢柱承载能力的影响.文献[6-7]研究发现,预应力撑杆钢柱不同阶屈曲荷载可能相当接近,并会发生不同屈曲模态之间相互影响的相关屈曲现象.文献[8]对设置双层撑杆的预应力撑杆钢柱相关屈曲展开了研究,结果表明此类双层撑杆结构可忽略相关屈曲影响.文献[9-10]对高性能钢材的单层预应力撑杆钢柱展开了研究,发现提高钢材强度后,预应力撑杆钢柱的稳定承载能力有所提高,但是这项研究仅是针对沿着柱高设置一层撑杆的情形展开的,且并未考虑撑杆长度、拉索直径和屈曲模态的影响.
本文以设置双层撑杆的预应力撑杆钢柱为研究对象,通过有限元软件ABAQUS进行数值分析,重点考察采用不同强度等级的钢材时,预应力撑杆钢柱的稳定性能,并分析其影响因素.
全文HTML
-
图 1为本文研究的预应力撑杆钢柱模型示意图,其中撑杆设置在柱高三等分点位置,柱和撑杆采用相同的圆管截面,其外径和壁厚分别为38.1 mm和6.35 mm.柱和撑杆采用的材料为钢材,其弹性模量为206 000 N/mm2,而拉索的弹性模量为160 000 N/mm2.本文分析时柱长设置为5 100 mm,中心柱与撑杆的连接形式为刚接,柱端约束形式为铰接约束,轴心受压荷载作用于柱上端.有限元分析时,柱和撑杆采用梁单元模拟,而预应力索采用桁架单元模拟.
根据撑杆长度和拉索直径的不同,本文共选取4个不同的模型进行研究,模型参数如表 1所示.其中,模型1和模型2的拉索直径为1.6 mm,模型3和模型4的拉索直径为8.0 mm;模型1的撑杆长度为255 mm,模型2和模型3的撑杆长度相同均为510 mm,模型4的撑杆长度为765 mm.
如前所述,本文重点研究钢材强度对预应力撑杆钢柱稳定性能的影响.为此,对于表 1所示的4种模型,本文对柱和撑杆均采用碳素结构钢Q235以及低合金高强度结构钢Q345,Q390,Q420和Q460 5种钢材进行分析,分析时钢材采用理想弹塑性模型.
-
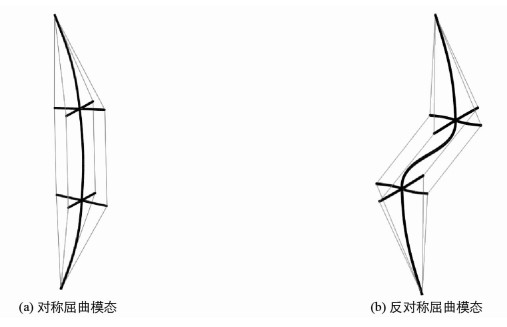
对本文研究的预应力撑杆钢柱进行线性屈曲分析表明,这类结构构件通常会呈现出图 2所示的对称和反对称屈曲模态.在对称屈曲模态中,中心柱的最大侧向挠度出现在柱跨中位置,而在反对称屈曲模态中,中心柱的最大侧向挠度出现在柱高三分之一(撑杆与中心柱交点)附近.
表 2列出了表 1所示4种模型的屈曲模态.其中,模型1和模型2为对称屈曲模态,模型3和模型4为反对称屈曲模态.由表 1可以看出,模型1和模型2的撑杆长度或者拉索直径小于模型3和模型4.因此,当撑杆长度或者拉索直径较小时,预应力撑杆钢柱呈现出对称屈曲模态,反之则为反对称屈曲模态.
-
初始缺陷是影响预应力撑杆钢柱稳定性能的一个重要因素,本文在数值分析时同样考虑了初始缺陷的影响.缺陷大小取为L/300(L为柱长),而缺陷分布假定与其最低阶线性屈曲模态相同.除了初始缺陷以外,拉索初始预应力也是影响预应力撑杆钢柱稳定性能的另一因素,本文采用文献[8]中的方法施加初始预应力.
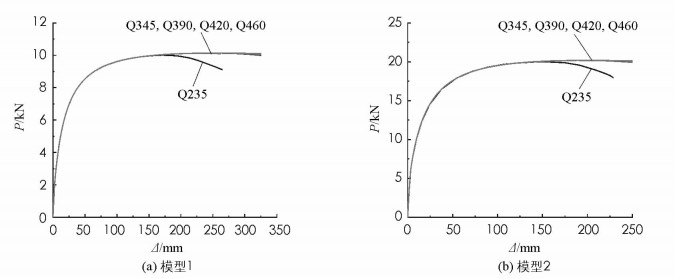
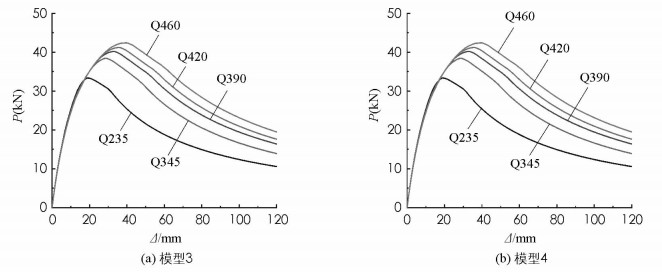
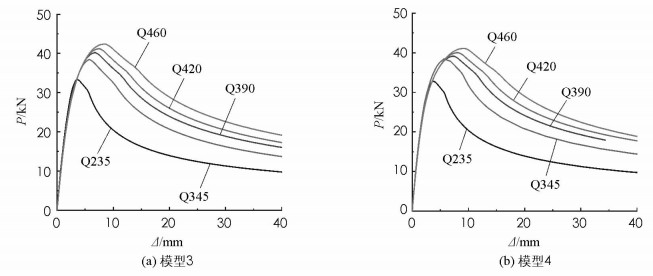
图 3和图 4所示分别为模型1和模型2、模型3和模型4在采用不同强度钢材时的荷载-挠度曲线.由于屈曲模态不同,对于图 3的模型1和模型2而言,其横轴所示的挠度表示柱中点处的挠度;而对于图 4所示的模型3和模型4而言,其横轴所示的挠度则为中心柱柱长三等分点处的挠度.可以看出,对于模型1和模型2而言,即对称屈曲模态下,提高钢材强度并不会显著提高预应力撑杆钢柱的承载能力.然而,提高钢材强度却可以显著提高模型3和模型4的承载能力.
表 3所示为4种模型在采用不同钢材的情况下结构屈曲时的挠度.与图 3和图 4相同,模型1和模型2采用的是跨中挠度作为表征指标,而模型3和模型4采用的是柱高三分之一处的挠度作为表征指标.可以看出,提升钢材强度,结构屈曲时对应的挠度随之增大.同时还可以发现,对于同一种强度的钢材而言,结构发生对称屈曲时的挠度远大于发生反对称屈曲时的挠度.
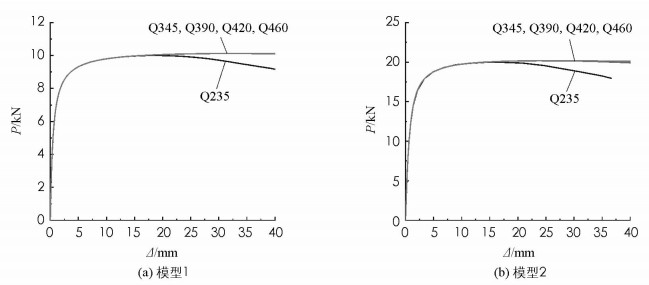
与图 3和图 4类似,图 5和图 6还给出了预应力撑杆钢柱的荷载-压缩曲线,其中横坐标所示的压缩为中心柱的轴向压缩.由图 5(a)和图 5(b)可以看出,模型2的承载能力总是高于模型1的承载能力,因此当结构发生对称屈曲时,增加撑杆长度可以提升预应力撑杆钢柱的承载能力.由图 6可以看出,当结构发生反对称屈曲时,撑杆长度的增加并不能明显提升预应力撑杆钢柱的承载能力.比较图 5(b)和图 6(a)可以发现,当撑杆长度不变增大拉索直径后,结构的承载能力显著提升.
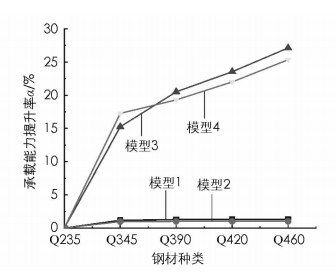
为了进一步分析钢材强度对预应力撑杆钢柱承载能力的提升作用,图 7给出了承载能力提升率随钢材强度的变化关系. 图 7纵轴所示的承载能力提升率α,表征某一强度钢材相对于Q235钢对应承载能力的提升率.可由式(1)计算:
式中,Pu表示某种钢材强度的预应力撑杆柱的承载能力,P0表示Q235钢材预应力撑杆柱的承载能力.可以看出,模型1和模型2对应的承载能力提升率不超过2%,而模型3和模型4对应的承载能力提升率最大则可以达到25%以上.因此,当结构为反对称屈曲时,提升钢材强度可以明显提高其承载能力;而当结构呈现出对称屈曲时,这种提升作用却不明显.
表 4所示为预应力撑杆钢柱发生屈曲时的轴向压缩量.显然,模型1和模型2在发生屈曲时的轴向压缩大于模型3和模型4.比较表 4和表 3还可以看出,预应力撑杆钢柱发生屈曲时的侧向挠度远大于其轴向压缩,即这类结构构件发生屈曲时的变形是以弯曲变形为主.
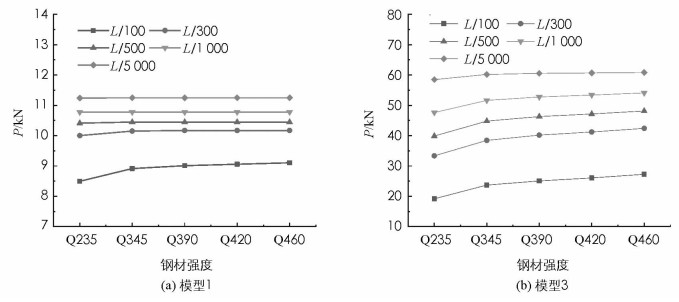
在上述分析中,初始缺陷大小取值为L/300,然而已有研究表明[5],预应力撑杆柱的承载能力受初始缺陷影响较大.为此,图 8选取了模型1和模型3,研究初始缺陷对不同钢材强度下结构承载能力的影响.缺陷大小取值分别为L/100,L/300,L/500,L/1 000,L/5 000.图中可以看出,随着初始缺陷的减小,结构承载能力显著增强,且模型3承载能力的提升程度远大于模型1,即模型3对初始缺陷更为敏感.
2.1. 线性屈曲分析
2.2. 非线性屈曲分析
-
1) 结构的屈曲模态决定了钢材强度与结构承载性能之间的关系,当结构发生对称屈曲时,提升钢材强度对结构稳定承载力并没有显著影响;当结构发生反对称屈曲时,钢材强度的提升使得结构承载性能明显增强.
2) 不同的撑杆长度和拉索直径,可能对结构的屈曲模态和承载性能产生显著影响.当撑杆长度或者拉索直径较小时,预应力撑杆钢柱呈现出对称屈曲模态,反之则为反对称屈曲模态;增大拉索直径,或当结构发生对称屈曲时增加撑杆长度,均可以有效地提升结构的承载性能.




 下载:
下载: