-
张量的特征值和特征向量是矩阵的特征值和特征向量的推广,在自动控制、数据统计、优化、图像处理、固体力学、量子纠缠和高维马尔科夫链中都有重要的应用[1-9].复数域上的m阶n维的张量定义为
矩阵伪谱是分析矩阵特征值扰动的重要工具,在控制理论、微分方程数值解等领域都有着举足轻重的应用[10-11].张量伪谱可以看成是矩阵伪谱的推广,它与齐次动力系统的稳定解息息相关[12].
令zm-1=λ,若Re(z) < 0,则齐次动力系统
存在渐近稳定解.为了进一步判断其动力系统是否存在渐近稳定解,利用张量伪谱的定义,文献[12]得到了张量伪谱的圆盘定理,张量伪谱圆盘定理中得到的区域包含所有张量伪谱中的特征值,并且经常被用来判断齐次动力系统渐近稳定解的存在性.
本文通过对张量伪谱的进一步研究,得到了包含张量伪谱的更小的新包含域,新包含域包含所有张量伪谱中的特征值.数值例子验证了结果的有效性.
令
ri(A)=∑(i2,⋯,im)≠(i,…,i)|aii2⋯im|,rji(A)=∑(i2,⋯,im)≠(i,⋯,i)|aii2⋯im|−|aij⋯j| ,可得如下张量伪谱的新包含域:定理1 设A=(ai1…im),E=(ei1…im)∈C[m,n],ε≥0.则
其中
证 令λ∈Λε(A),设非零向量x∈
C n是特征值λ对应的特征向量,即令|xp|=max{|xi|:i∈N},则|xp|≠0,其中N={1,2,…,n}.
若向量x中只有xp≠0,由(3)式可得
在等式(4)两边同时取绝对值,有
由Hölder不等式,有
由(5)式可得
即λ∈Λε(A)⊆Δ1(A)⊆Δ(A).
若向量x中至少有两个元xp≠0,xq≠0(p≠q),则有
求解xpm-1,有
在等式(6)两边同时取绝对值,有
即
即λ∈Λε(A)⊆Δ2(A)⊆Δ(A).
定理2 设A=(ai1…im),E=(ei1…im)∈C[m,n],ε≥0,则Δ(A)⊆D(A).
证 情形1 若λ∈Λε(A)⊆Δ1(A),由定理1可得
即λ∈D(A).
情形2 若λ∈Λε(A)⊆Δ1(A),由定理1知,存在p≠q,使得
又因为
则
即
若
|apq⋯q|(rp(A)+nm−12ε)=0 ,则有即有λ∈D(A).若
|apq⋯q|(rp(A)+nm−12ε)>0 ,则有即
或者
也就是说,λ∈Dp(A)或者λ∈Dq(A).即λ∈D(A).
注1 由定理2的结论可知,定理1得到的张量伪谱新包含域比文献[12]中定理3.1的包含域好,但是表达式更复杂,计算量更大.
我们用数值例子来说明结果的有效性.
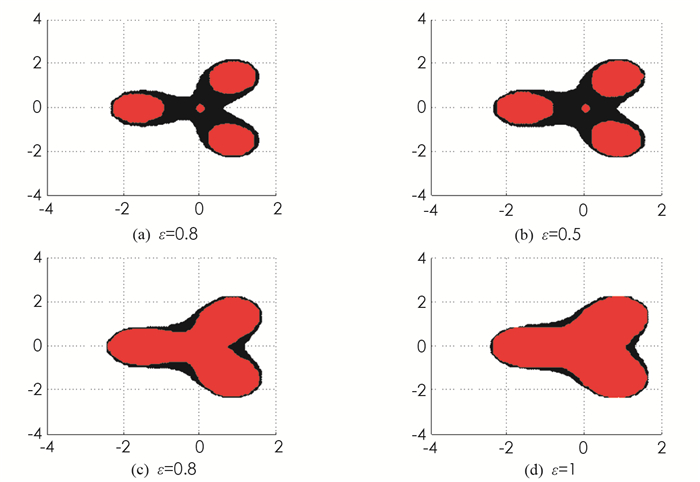
其余的aijkl=0.令zm-1=λ,ε=0.4,0.5,0.8,1,在图 1中,我们给出关于z的包含区域,文献[12]的定理3.1中张量伪谱区域D(A)用黑色表示,定理1中张量伪谱区域Δ(A)用红色表示.由图 1可以看出,定理1的结果比文献[12]中定理3.1的结果好.
Pseudo-spectrum Localization Sets of Tensors
-
摘要: 张量伪谱可以看成是矩阵伪谱的推广,它在齐次动力系统中有着重要的作用.对张量伪谱圆盘定理进一步研究.利用张量伪谱中特征向量的最大元,给出了张量伪谱的新包含域.数值例子验证了结果的有效性.Abstract: The definition of pseudo-spectrum of tensors can be seemed as a generation of the definition of pseudo-spectrum of matrices, which plays important role in the homogeneous dynamical system. The pseudospectra localization of tensors is often used to determine the existence of its asymptotically stable solution for the homogeneous dynamical system. In this paper, a new pseudospectra localization of tensors is established by the maximum element of the eigenvector. Numerical experiments are reported to show effectiveness of our results.
-
Key words:
- tensor /
- pseudo-spectrum /
- localization set .
-
植物群落的物种之间不是孤立存在的,多个物种之间或依存、或竞争,彼此共同进化最终达到相对稳定的状态[1].种间关联是群落重要的数量和结构特征之一,反映了不同物种在空间及数量分布上的彼此相关性[2].近些年来,通过探讨物种间的相互作用来分析个体生存、发展、群落稳定程度[3-4],越来越受到生物学家尤其是群落生态学家的重视[5].相对于群落的生态位分析,种间关联能更加直接地反映物种间的有机联系和群落动态,在研究物种的濒危机制、揭示群落竞争状况及演替趋势等方面具有重大意义[6-7].
缙云秋海棠(Begonia jinyunensis)为缙云山特有珍稀濒危物种,其花朵大而艳丽,叶型变异大,观赏价值较高.随着近年来缙云山旅游业的兴起,缙云秋海棠不断遭到游客的采摘和挖掘,种群呈明显衰退趋势,生境破坏日趋严重,生存现状堪忧.本研究拟以包含缙云秋海棠的7个群落为研究对象,分析缙云秋海棠在群落中的地位以及与主要伴生种的相互作用关系,试从种间关联的角度探讨并回答以下问题:一,相关群落的稳定程度对缙云秋海棠生存有何种影响?二,关联度反映的物种之间的相互作用是否是导致缙云秋海棠濒危的原因之一?本研究的开展有助于增进对缙云秋海棠濒危原因的理解,为缙云秋海棠的保护及种群恢复有重要意义.
1. 研究地自然概况
研究地位于重庆市北碚缙云山国家级自然保护区,海拔在180~951.5 m[8]之间,总占地面积76 km2[9].保护区内属典型亚热带季风湿润气候,年平均气温13.6 ℃,月平均气温最高为24.3 ℃,最低气温为3.1 ℃,年平均降水量1 143 mm[10].区内环境多样,地带性植多样,多种典型的生态系统并存,物种多样性极为丰富,森林覆盖率达96.6%[11],为长江流域保存较完好的植物种质基因库[12],形成了包括缙云秋海棠(Begonia jinyunensis)、缙云黄芩(Scutellaria tsinyunensis)、缙云卫矛(Euonymus chloranthoides)等一批特有珍稀濒危植物.本研究选择缙云秋海棠相对集中的7个群落(图 1),海拔均位于600~800 m之间,多处于相对阴暗的沟边或林下,部分样地人为干扰程度较大.
2. 研究方法
2.1 样地调查与样方设置
2017年1月中旬,在预调查的基础上,选定7个缙云秋海棠代表性群落进行结构和特征研究. 7个群落均为典型的常绿阔叶林,乔木层主要为四川山矾,灌木层物种组成及数量也较为相似.缙云秋海棠为多年生草本,株高多在20~40 cm之间.因此仅对7个群落内草本层植物(包括层间植物)进行调查,根据7个群落所处的地形、地貌、位置等差异,结合缙云秋海棠的数量及分布,以5 m×5 m为单位行样方设置.再根据Smith提出的“棋盘格子法”并将单位样方划分为1 m×1 m的小样方[13].样地环境资料如表 1所示.
表 1 样地的环境资料群落代号 样地名称 海拔/m 坡度/° 坡向/° 郁闭度 人为干扰强度 群落类型 Ⅰ 雷氏A栋 742.0 24.3 78 0.90 + 常绿阔叶林 Ⅱ 雷氏A栋Ⅰ 727.0 27.0 105 0.85 ++ 常绿阔叶林 Ⅲ 雷氏A栋Ⅱ 736.3 17.5 161 0.90 + 常绿阔叶林 Ⅳ 雷氏A栋Ⅲ 725.0 18.0 294 0.75 ++ 常绿阔叶林 Ⅴ 缙云寺 724.0 22.5 138 0.60 + 常绿阔叶林 Ⅵ 良缘山庄 725.7 15.0 30 0.80 + 常绿阔叶林 Ⅶ 缙云小学 687.0 20.0 310 0.90 ++++ 常绿阔叶林 注:(1)坡向数据是以朝东为起点(即为0°)逆时针旋转的角度表示,采取45°为1个区间划分等级制的方法,东北坡22.5°~67.5°,北坡67.5°~112.5°,西北坡112.5°~157.5°,西坡157.5°~202.5°,西南坡202.5°~247.5°,南坡247.5°~292.5°,东南坡292.5°~337.5°,东坡337.5°~382.5° (2)+,无干扰;++,轻度干扰;+++,中度干扰;++++,重度干扰 2.2 数据处理
记录7个样地各小样方所有草本层植物的种类、多度、盖度等指标,先分别计算各样地中某一种群的重要值,在此基础上再统计出7个样地的总和作为该物种的重要值.取包括缙云秋海棠在内及重要值>0.05的植物进行种间关联性分析.重要值(Importance Value)的计算公式[14-15]为:
IV=(相对密度+相对频度+相对盖度)/3
式中:相对密度(%)=100×某个物种的株数/所有物种的株数;相对频度(%)=100×某个种出现的样方数/所有种出现的样方数之和;相对盖度(%)=100×某个种的分盖度/所有种的分盖度之和.
2.3 群落中种间关联性分析
2.3.1 多物种间总体关联性检验
应用方差比率法(variance ratio,VR)进行计算[16],公式如下:
δT2=S∑i=0Pi(1−Pi);Pi=ni/NST2=S∑k=01N(Tj−t)2VR=δT2ST2 式中:S为调查区总物种数;N为总样方数;Tj为样方j内出现的研究物种总数;ni为物种i出现的样方数;t为全部样方中种的平均数,t=(T1+T2+...Tn)/N.
VR的期望值在符合独立性假设的情况下为1.若VR=1,物种间总体关联无统计学意义;若VR>1,物种间总体呈正关联;若VR < 1,物种间总体呈负关联.由于种间正负关联可以相互抵消,根据统计量W=VR×N数值的大小,结合特定的范围对VR值偏离1的显著程度进行判定[17].若种间关联无统计学意义,由W落入卡平方分布给出的界限(χ0.952(N)<W<χ0.052(N))内的概率为90%[18].
2.3.2 物种间关联性检验
根据种对在样方中出现与否的数据建立2×2列联表[19],代入χ2公式计算,检测成对物种间的种间关联性,计算公式为[2]:
χ2=N(ad−bc)2(a+b)(c+d)(a+c)(b+d) 样方数量小或取样非连续时,需用Yates的连续校正系数进行计算并取值[20],按以下公式计算:
χ2=N(|ad−bc|−N2)2(a+b)(c+d)(a+c)(b+d) 式中:N为总样方数;a为两个物种均出现的样方数;b为仅物种A出现而物种B不出现的样方数;c为仅物种B出现而物种A不出现的样方数;d为两个物种均不出现的样方数.种间关联有无统计学意义的判断标准:
2×2列联表的自由度为1,若χ2<χ0.052(1)=3.841时,各物种间是相互独立的;当χ0.052(1)<χ2<χ0.012(1)=6.635时,物种间关联性有统计学意义;当χ2>χ0.012(1)=6.635时,物种之间关联性极有统计学意义.仅根据上述规则无法判断正负关联,正负关联由ad-bc的值决定. ad-bc=0时,两物种间彼此独立无关联;ad-bc>0为正相关;ad-bc < 0为负相关.
2.3.3 物种间关联程度测定
χ2检验不能区分联结程度的大小,模糊了种间关联性的差异性[17].采用Ochiai指数(OI)、Dice指数(DI)和Jaccard指数(JI)进行种间关联程度测定,公式如下[20],其中a,b,c,d的含义与上述相同:
OI=a√a+c/¯a+bDI=2a2a+b+cJI=aa+b+c 式中:OI,DI,JI 3个指数均描述种对间同时出现的几率并以此反映关联强弱程度,实为平行验证.当a=0时,3个指数取值均为0,可能是竞争极度激烈或对生境的要求显著不同,导致物种几乎不相伴出现;当a=S(总种数)时,表明物种间呈紧密关联状态,始终同时出现[21-22].相对于应用种间联结系数(AC)测定种间关联程度,OI,DI,JI在种数较多和取样数目较大时能避免d值高而导致AC偏高的特点,能更好地反映关联性不明显的物种间共同出现的概率及联结性的强弱[5].
3. 结果与分析
3.1 群落主要物种调查
7个群落共计732个小样方(部分小样方无植物,未计入内),调查并记录152个物种.其中,除缙云秋海棠外,重要值大于0.05的植物有14种.选定的进行种间关联性分析的15个主要物种如下(表 2).为呈现缙云秋海棠在群落中的地位及重要程度,特将其列出(表 3).
表 2 缙云秋海棠群落中的15个主要物种物种代号 种名 1 缙云秋海棠 Begonia jinyunensis 2 石生楼梯草 Pellionia radican 3 斜方复叶耳蕨 Arachniodes rhomboidea 4 异药花 Fordiophyton faberi 5 常春藤 Hedera nepalensis 6 竹叶草 Oplismenus compositus. 7 过路黄 Lysimachia christinae 8 大叶仙茅 Curculigo capitulate 9 对马耳蕨 Polystichum tsus-simense 10 蝴蝶花 Iris japonica 11 寒莓 Rubus buerger 12 狗脊 Woodwardia japonica 13 透茎冷水花 Pilea pumila 14 纤细半朔苣苔 Hemiboea cavaleriei 15 紫萁 Osmunda japonica 表 3 缙云秋海棠群落中在7个群落中的重要值群落代号 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ 重要值/% 4.7 17.4 1.8 8.4 21.4 9.3 8.6 3.2 多物种间总体关联性分析
群落主要物种间总体关联性衡量的是物种之间的静态关系,与群落的稳定性密切相关[22-23],亦能反映群落的演替方向[24].研究表明,群落结构及其种类组成会随着植物群落的不断演替而逐步趋于稳固和完善,以利于物种间的稳定共存,物种之间也多呈现为正相关[25].群落间主要物种总体关联性分析计算统计结果如表 4所示.
表 4 主要物种间的整体关联性分析群落 δT2 ST2 方差比率 检验统计量 χ2临界值 测度结果 Ⅰ 2.63 0.89 2.96 739.56 (214.39,287.88) +** Ⅱ 6.91 1.15 6.00 149.94 (14.61,37.65) +** Ⅲ 1.32 0.63 2.08 416.62 (168.28,233.99) +** Ⅳ 1.70 1.33 1.28 31.99 (14.61,37.65) + Ⅴ 14.06 1.15 12.24 514.05 (28.14,58.12) +** Ⅵ 5.56 0.70 7.90 789.24 (77.93,124.34) +** Ⅶ 5.43 0.72 7.55 679.83 (69.13,113.15) +** 注:*(p < 0.05),**(p < 0.01) 结果表明,缙云秋海棠所在7个群落的方差比率(VR)均大于1,即多物种间呈正相关关系,群落演替已达到相对稳定的状态.其中除群落Ⅳ(雷氏A栋Ⅲ)之外,其余6个群落检验统计量W均未落入χ2临界值范围内,即VR值显著偏离1,多物种间整体正相关有统计学意义.
3.3 缙云秋海棠与主要伴生物种种对间关联性检验
缙云秋海棠与主要伴生物种种对间关联性检验如表 5所示.
表 5 各群落缙云秋海棠与伴生物种种间关联性χ2统计检验和关联指数群落 物种对 关联性 χ2值 χ2连续校正值 关联指数 OI DI JI Ⅰ 1-2 + 0.679 2 0.303 1 0.179 1 0.179 1 0.098 4 1-3 - 1.483 8 1.047 8 0.163 3 0.144 0 0.077 6 1-4 +** 11.032 5 9.677 0 0.356 7 0.330 1 0.197 7 1-5 + 3.598 8 2.871 7 0.295 7 0.270 3 0.156 3 1-12 + 0.459 6 0.146 9 0.130 6 0.122 4 0.065 2 Ⅱ 1-3 + 2.706 8 1.501 9 0.623 6 0.608 7 0.437 5 1-6 + 1.417 8 0.585 9 0.527 0 0.526 3 0.357 1 1-7 + 0.184 9 0.114 2 0.235 7 0.181 8 0.100 0 1-8 - 0.694 4 0.097 7 0.149 1 0.142 9 0.076 9 1-9 - 0.529 1 0.074 4 0.239 0 0.235 3 0.133 3 Ⅲ 1-2 - 0.882 0 0.219 0 0.076 2 0.060 6 0.031 3 1-10 + 0.887 9 0.309 3 0.259 9 0.135 6 0.072 7 1-11 + 1.197 4 0.178 5 0.218 4 0.152 2 0.082 4 Ⅳ 1-2 + 0.446 4 0.012 4 0.338 1 0.333 3 0.200 0 1-6 -* 5.468 8 3.513 9 0 0 0 1-10 + 0.005 2 0.142 0 0.404 1 0.381 0 0.235 3 1-11 - 1.989 6 0.896 0 0.126 0 0.125 0 0.066 7 1-15 + 1.143 2 0.213 2 0.378 0 0.363 6 0.222 2 Ⅴ 1-3 - 1.493 3 0.749 3 0.333 3 0.307 7 0.181 8 1-10 - 2.670 4 1.590 5 0.248 1 0.222 2 0.125 0 1-13 + 0.597 9 0.163 4 0.442 7 0.400 0 0.250 0 1-14 + 0.148 2 0.004 1 0.326 6 0.258 1 0.148 1 Ⅵ 1-2 + 2.150 8 1.489 2 0.693 0 0.683 8 0.519 5 1-13 - 0.275 4 0.552 7 0.457 9 0.449 4 0.289 9 Ⅶ 1-10 -** 1.550 5 22.653 5 0.353 2 0.352 9 0.214 3 1-12 + 1.500 1 0.724 9 0.272 8 0.200 0 0.111 1 注:*(p < 0.05),**(p < 0.01) 结果表明,在26对物种对中,呈正关联的有16对,其中仅1对正相关有统计学意义,呈负关联的有10对,其中1对负相关有统计学意义,1对负相关极有统计学意义.正关联的种对多于负关联的种对,与物种间总体为正关联的结果一致. 26个种对间有23个关联无统计学意义,说明缙云秋海棠群落主要伴生种种间联结相对松散,物种分布具有一定的独立性,群落处于相对稳定的状态.
3.4 物种间关联程度分析
OI,DI,JI 3个指数均能表征种间关联程度的大小且彼此具有较高的相似性,取OI值进行关联程度分析.对于正关联而言,关联指数越大,关联性越紧密,正关联性越强.负关联则相反,关联指数越小,负关联性越强[26].
在缙云秋海棠群落主要草本植物组成的16个正关联种对中,种间关联测度值均小于0.7.其中OI>0.6的种对有2对,占正关联总对数的12.5%,0.4≤OI < 0.6的种对有3对,占正关联总对数的18.7%,其余的11对物种的OI值均在0.4以下,占正关联总对数的68.8%.说明多数正关联种对间的关联性不强,联结相对较弱,物种趋于独立分布,与χ2检验所得结果一致.在10个负关联种对中,种间关联测度值均小于0.5.其中,0.4≤OI < 的种对仅1对,占负关联总对数的10.0%,0.2≤OI < 0.4的种对有5对,占负关联总对数的50.0%,OI值在0.2以下的有4对,占负关联总对数的40.0%.负关联种对对数较正关联少,但种对间联结性相对较强.其中群落Ⅳ中竹叶草和缙云秋海棠的OI值为0,表明竹叶草和缙云秋海棠的负相关性极强,不在同一个样方中出现.
4. 结论与讨论
多物种间总体关联性分析表明,缙云秋海棠所在群落表现为正相关,群落处于动态演替的稳定阶段;成对物种间关联性检验表明,正关联种对数多于负关联种对数,大多数种对间关联性无统计学意义,呈现独立分布格局;物种间关联程度分析表明,正关联种对间联结性较弱,负关联种对间联结相对较紧密,总体而言种间联结仍较为松散.
从种间关联性看,大部分群落物种正相关有统计学意义,说明群落内各种群间联结紧密,已形成多物种共存复杂而稳定的群落,利于缙云秋海棠的生存;同时,缙云秋海棠和其主要伴生种虽然有大体一致的生境需求,但相似的资源利用策略并未导致种对间强烈的竞争,目前物种间相容性良好,群落稳定发展.即群落中物种间的相互作用不是导致缙云秋海棠濒危的主要原因.
研究发现,缙云秋海棠喜阴湿,仅与异药花、蝴蝶花等少数物种间关联性极有统计学意义.群落Ⅰ中缙云秋海棠和异药花正相关极有统计学意义.异药花多生活在海拔600~1 100 m林下,沟边或遮阴灌木丛等较为潮湿的地方[27],与缙云秋海棠有着相似的生境需求和生态习性.但群落Ⅰ郁闭度较大,人为干扰程度较小,环境资源相对丰富,二者尚未出现竞争而呈现出正向关联性.群落Ⅶ的样方取样不连续,故参考χ2连续校正值进行判断.其中,蝴蝶花与缙云秋海棠负相关极有统计学意义,其生境[28]与缙云秋海棠相似,但蝴蝶花在弱光下即可很好地生长,生存能力较强.此外,群落Ⅶ有践踏的小路,遭到较为严重的人为干扰,因而在环境资源匮乏的情况下,二者之间产生激烈竞争,表现为负相关极有统计学意义.可见人为干扰不仅直接威胁其生存,使其数量骤减,也加剧了其与伴生物种间的竞争.群落Ⅳ中竹叶草也与缙云秋海棠表现出极强负相关,竹叶草多生长在山地、丘陵、疏林下阴湿处,与缙云秋海棠的生境具有一定相似性.可能在资源不充足的情况下,两者产生了较激烈的竞争,或是他感作用使两者相互排斥最终形成此种分布格局.
此外,同一种对在不同群落中的相关性和联结性均有所差异.以缙云秋海棠和斜方复叶耳蕨为例,二者在群落Ⅱ中二者呈正相关关系,且联结性较强;在群落Ⅰ、Ⅵ中则表现为负相关.原因是不同群落中温度、光照、水分、土壤等诸多环境因子存在较大差异,从而影响了物种间的相互作用[29].在群落Ⅱ中,缙云秋海棠的生长状况良好,重要值为17.4%,优势度较高,分布范围相对较广;而群落Ⅰ、Ⅵ中的缙云秋海棠的重要值分别为4.7%和8.4%,优势度相对较低,分布较为局限.笔者认为,物种间的正负关联性并不完全是生境偏好差异或种间排斥的结果,在特定的空间资源条件下,物种本身生长状况和扩散能力也会影响种间关联性结果的测定.
缙云秋海棠作为重庆缙云山发现的特有珍稀植物,研究并探索其濒危原因有重要意义.经调查发现,其目前仅在缙云山青龙寨、石华寺、园艺场等以及一些阴湿沟谷两边有居群,分布地狭窄.花期在7月份[30],仅为2周左右,自然繁殖能力较弱.调查结束时,发现群落Ⅶ的破坏程度进一步加剧,样地中缙云秋海棠的数量急剧减少.因此,缙云秋海棠种群极有可能会因为自身繁殖特性的限制和人为破坏进一步衰退.该物种亟待加强保护,一方面,建议相关部门积极采取措施,进一步展开实地考察,统计现存数量,对其生存现状和濒危状态进行评估,加大宣传和保护力度,对主要群落加强管理,严禁游客采挖;另一方面,采用多种手段展开种群扩繁研究,如探索组织培养、种子萌发的适宜条件等,以利于种群的更新和扩繁.
-
[1] QI L Q.Eigenvalues of a Real Supersymmetric Tensor[J].Journal of Symbolic Computation, 2005, 40(6):1302-1324. doi: 10.1016/j.jsc.2005.05.007 [2] doi: http://d.old.wanfangdata.com.cn/Conference/8576630 LI C Q, LI Y T, KONG X.New Eigenvalue Inclusion Sets for Tensors[J].Numerical Linear Algebra with Applications, 2014, 21(1):39-50. [3] LI C Q, CHEN Z, LI Y T. A New Eigenvalue Inclusion Set for Tensors and Its Applications[J].Linear Algebra and its Applications, 2015, 481:36-53. doi: 10.1016/j.laa.2015.04.023 [4] LI C Q, WANG F, ZHAO J X, et al.Criterions for the Positive Definiteness of Real Supersymmetric Tensors[J].Journal of Computational and Applied Mathematics, 2014, 255:1-14. doi: 10.1016/j.cam.2013.04.022 [5] BU C J, WEI Y P, SUN L Z, et al.Brualdi-Type Eigenvalue Inclusion Sets of Tensors[J].Linear Algebra and its Applications, 2015, 480:168-175. doi: 10.1016/j.laa.2015.04.034 [6] BU C J, JIN X Q, LI H F, et al.Brauer-Type Eigenvalue Inclusion Sets and the Spectral Radius of Tensors[J].Linear Algebra and its Applications, 2017, 512:234-248. doi: 10.1016/j.laa.2016.09.041 [7] 桑彩丽, 赵建兴.非负矩形张量最大奇异值的S-型上界[J].西南师范大学学报(自然科学版), 2018, 43(6):1-5. doi: http://d.old.wanfangdata.com.cn/Periodical/xnsfdxxb201806001 [8] 钟琴.非负矩阵最大特征值的新界值[J].西南大学学报(自然科学版), 2018, 40(2):40-43. doi: http://d.old.wanfangdata.com.cn/Periodical/szjsyjsjyy200204007 [9] 钟琴, 周鑫, 牟谷芳.非负矩阵谱半径的上界估计[J].西南大学学报(自然科学版), 2017, 39(6):50-53. doi: http://d.old.wanfangdata.com.cn/Periodical/xnsfdxxb201602002 [10] TREFETHEN L N. Spectra and Pseudospectra:The Behavior of Nonnormal Matrices and Operators[J].Bulletin of the American Math Society, 2005(2):277-284. [11] BOSE N. Test for Lyapunov Stability by Rational Operations[J]. IEEE Trans Automat Control, 1975, 20(5):700-702. doi: 10.1109/TAC.1975.1101045 [12] CHE M L, LI G Y, QI L Q, et al.Pseudo-Spectra Theory of Tensors and Tensor Polynomial Eigenvalue Problems[J].Linear Algebra and its Applications, 2017, 533:536-572. doi: 10.1016/j.laa.2017.07.026 -





 下载:
下载: