下面介绍符号模式矩阵和符号二部图的一些重要定义.

定义1^[3]  设A=(a_ij)是一个n阶实矩阵，以a_ij的符号{+，-，0}为元素所组成的矩阵称为A的符号模式矩阵，记为P.记与A有相同符号模式的所有实矩阵所组成的集合称为由A所决定的定性矩阵类，记为Q(A).

定义2^[4]  设P是一个n阶的符号模式矩阵，P的最小秩定义为：

其中min表示最小值.

定义3^[9]  一个图G由有限的非空顶点集V和边集E两部分组成.图G的阶数是G的顶点个数，记为|G|.一个若无重边和环的图称为简单图.

定义4^[9]  在一个无向图G=(V，E)中，边集{{i₁，i₂}，…，{i_k-1，i_k}}的各个顶点都不同称为从点i₁到点i_k的一条路，k为路长.若i₁与i_k重合则称{{i₁，i₂}，…，{i_k-1，i_k}}为圈.

定义5^[9]   不含任何圈的图称为无圈图，树就是无圈图.

定义6^[9]   一个有向图是由非空有限集合V与集合E构成，记为Γ，其中V中元素为顶点，E中元素为不同顶点的有序对，称为弧或有向边.

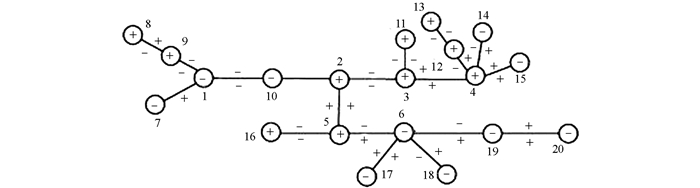
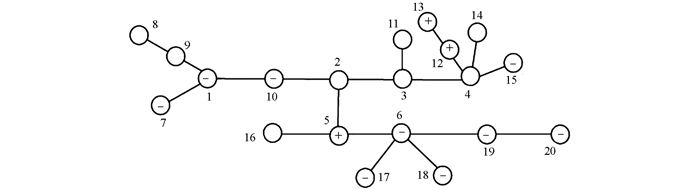
定义7^[5]  设P为一符号模式矩阵，G为P的伴随图.若图G中的每边都带有符号，则称G为符号图，记为G=(V，E，sign)，其中sign是边集E与集合{1，-1}的一个映射.若P中元素为正，则E中所对应的边为“+”，记为sign(e)=1；若P中元素为负，则E中所对应的边为“-”，记为sign(e)=-1.若G中的{i，j}与{j，i}具有相同的符号，称G为对称符号图.否则称为非对称符号图.若G为树，分别称为对称符号树与非对称符号树(图 1^[6]与图 2).

定义8^[9]  若图G的顶点集V能够被分为两个子集U，V(称为部集)，使得G的每条边必连接U中一个顶点和V中一个顶点(记边集为E(G))，称G为二部图，记为G(U，V).

定义9^[9]  设M是E(G)的子集，如果M中任意两条边在G中均不邻接，则称M是G(U，V)的一个匹配，并记M所含的边数为|M|.

定义10^[5]  设G(U，V)为二部图，P为一符号模式矩阵，其中U={1，2，…，n}(对应P的行标集)和V={1′，2′，…，n′}(对应P的列标集).若图G中的每边都带有符号，则称G为符号图，记为G=(V，E，sign). G(U，V)每边的符号由P的符号来确定，若sign(e)=1，则边{i，j′}标为“+”，i∈U，j′∈V；若sign(e)=-1，则边{i，j′}标为“-”，i∈U，j′∈V；若在P中元素为零，则在G(U，V)中不存在边.

定义11  设G(U，V)=(V，E，sign)为符号二部图.若边sign(e)=1，则有向边{i，j′}∈E，i∈U，j′∈V；若sign(e)=-1，则有向边{j′，i}∈E，i∈U，j′∈V. G(U，V)称为有向二部图.

定义12  在有向二部图G(U，V)中，若{i，j′}∈E，称j′是i的一个“外邻居”点.若{j′，i}∈E，称j′是i的一个“内邻居”点.顶点i的所有“外邻居”点的个数，称为i的出度，记为deg⁺(i)；顶点i的所有“内邻居”点的个数，称为i的入度，记为deg^-(i).在U(V)的所有顶点中，U(V)的最小出度记为δ⁺(V)(δ⁺(U))，U(V)的最小入度记为δ^-(U)(δ^-(V)).

本节结合文献[5]的符号二部图和文献[6]的算法，研究了对称符号树和非对称符号树的最小秩问题，并提供了计算符号树的有效算法，从而获得了符号对称树与符号非对称树的最小秩.

设P是一个n阶符号模式矩阵，其伴随图为符号树，P的最小秩也称为符号树的最小秩.因此，借助P的伴随图来研究其最小秩问题.

下面介绍符号模式矩阵的符号特征与其伴随图之间的关系.

定义13^[3]  设符号模式矩阵P=(p_ij)是方阵，{i₀，i₁}，{i₁，i₂}，…，{i_k，i₀}是其符号有向图Γ′中的一个圈γ，将圈γ的每条边作乘积，记为

称sign(γ)为γ的符号.若sign(γ)=+1，γ的符号为正；若sign(γ)=-1，γ的符号为负.

定义14^[5]  在符号二部图G(U，V)中，若任意两条边与V中同一顶点连接，且两条边符号相同，称这两条边为一个c-pair.若在一个圈中含有偶数(或奇数)个c-pairs，称此圈为e-圈(或o-圈).

定义15^[5]  在G(U，V)中，设M是P中主对角元素所对应的完美匹配.若一个圈的一条边在M中，此外一条边不在M中，则称为M-交替圈.

引理1^[5]  设在符号有向二部图G(U，V)中的完美匹配为M，且τ₁，τ₂，…，τ_m(τ_i=τ_i1τ_i2…τ_itiτ_i1，i=1，2，…，m)是m个不相交的M-交替圈，则

引理2^[5]  设P是n阶符号模式矩阵，其每一主对角元素非零，detP为P的行列式的展开式.设G(U，V)是P的符号二部图，M是P中主对角元素所对应的完美匹配，则：

(1) detP的非零项数t(P)等于G(U，V)中不相交M-圈的个数；

(2) 设ε为P的所有主对角元素的符号乘积的符号，则在detP中，符号为-ε的项数为所有不相交的M-交替圈中含有奇数个M-交替e圈的个数.

根据引理1和引理2，可以得到如下的推论.

推论1  设P是n阶符号模式矩阵，其每个主对角元素非零.设G(U，V)是P的符号二部图，M是P中主对角元素所对应的完美匹配，则在P的行列式的展开式中，非零项数(非零项记为x)t(P)是G(U，V)不相交的M-圈的个数.设ε为P的所有主对角元素的符号乘积的符号，则在P的行列式的展开式中，符号与ε相同的非零项的项数是所有不相交的M-交替圈中含有偶数M-交替e圈的个数.

下面由引理1、引理2和推论1提供计算符号树最小秩的算法，从而获得对称符号树与非对称符号树的最小秩.

算法1  设P为n阶符号模式矩阵，其伴随图为对称的(或非对称的)符号树T.设H为T的高度顶点集，其中，若deg(i)≥3(deg⁺(i)≥3或deg^-(i)≥3) 的顶点i称为高度顶点，将T转换为有向二部图G(U，V)

若H≠ϕ：

第一步：寻找只含有一个高度顶点的团树T_1j，P_1j为T_1j的符号模式矩阵，设高度顶点集为H₁≠ϕ；

1) 若T_1j所对应的有向二部图为G_1j(U_1j，V_1j)，M_1j为P_1j主对角元素所对应的完美匹配.

找出m个不相交的M_1j-交替圈τ₁，τ₂，…，τ_m(τ_i=τ_i1τ_i2…τ_itiτ_i1，i=1，2，…，m)，并在m个不相交圈中，计算e圈的个数k.若k为奇数，且e圈中含有T_1j的高度顶点.则删除G_1j(U_1j，V_1j)的顶点集U_1j中的高度顶点(P_1j中所对应的行).否则，转2)；

2) 若e圈中无高度顶点，删除G_1j(U_1j，V_1j)的顶点集U_ij中的非高度顶点；

3) 若在G_1j(U_1j，V_1j)的k(k为奇数)个不相交圈M_1j-交替e圈中，既含有高度顶点，也含有非高度的顶点，则删除G_1j(U_1j，V_1j)的顶点集U_1j中的高度顶点和V_1j中所对应的非高度顶点(P_1j中所对应的列)，破除e圈；

4) 若G_1j(U_1j，V_1j)中不含有不相交的M_1j-交替e圈，且T_1j的高度顶点与相邻团树的高度顶点不构成e圈，将两相邻团树构成一个新的团树.

在所有的G_1j(U_1j，V_1j)中，设删除U_1j的顶点集为R₁(对应P的行集)和V_1j的顶点集为L₁(对应P的列集).在T中，当删除这些顶点后，得到的树设为T₁，T₁所对应的有向二部图为G₁(U₁，V₁)，与之对应的符号模式矩阵为P₁；

若T₁中无高度顶点，停止；否则，转入第二步；

第二步：在T₁中找出只含有一个高度顶点的团树T_2j，P_2j为T_2j的符号模式矩阵，设高度顶点集为H₂≠ϕ.再转入第一步.在所有的G_2j(U_2j，V_2j)中，设删除U_2j的顶点集为R₂(对应P₁的行集)和V_2j的顶点集L₂(对应P₁的列集)，在T₁中，当删除这些顶点后，得到T₂；

设T₂所对应的有向二部图为G₂(U₂，V₂)，与之对应的符号模式矩阵为P₂.

第三步：在T₂中，若含有高度顶点，转入第二步.否则，在G₂(U₂，V₂)中的顶点集U₂(或V₂)中找孤立点和具有相同的“内邻居”点(或“外邻居”点)的顶点.若有，删除孤立点和其中具有相同的“内邻居”点(或“外邻居”点)的顶点.在G(U，V)中，设删除U的顶点集为R(对应的P行集)和V的顶点集为L(对应的P列集)后，得到有向二部图G′(U′，V′)，与之对应的符号模式矩阵为P′.

定理1  设P为n阶符号模式矩阵，其伴随图为(对称的或非对称的)符号树T.根据算法1，则mr(P)=n-k，其中，k=max{|R|，|L|}.

证  设H为T中高度顶点集，G(U，V)为T的有向二部图.在有向二部图为G_ij(U_ij，V_ij)中，M_ij为P_ij主对角元素所对应的完美匹配.若在m个不相交的M_ij-交替圈τ₁，τ₂，…，τ_m(τ_i=τ_i1τ_i2…τ_itiτ_i1，i=1，2，…，m)中，M_ij-交替e圈的个数为偶数，由推论1知，P_ij是非奇异的；若e圈的个数为奇数，由算法1的第一步和第二步，删除不相交的M_ij-交替e圈τ_i=τ_i1τ_i2…τ_itiτ_i1中的顶点，以致于破除e圈.在G(U，V)中，设删除U的顶点集为R(对应的P行集)和V的顶点集为L(对应的P列集)后，得到有向二部图G′(U′，V′)，与之对应的符号模式矩阵为P′.若在G′(U′，V′)中既无孤立点，也无相同的“内邻居”点(或“外邻居”点)的顶点，则在P′中既无全零的行(或列)和元素相同的两行(或列)，则P′为非奇异的符号模式矩阵.因此，mr(P)=n-k，其中，k=max{|R|，|L|}.

下面利用算法1分别计算对称符号树的最小秩(图 1)和非对称符号树的最小秩(图 2).

例1  计算图 1中对称符号树T的最小秩.

解：T中每个顶点处的符号(对应于符号模式矩阵P的主对角元素)如图 1所示，若无符号显示，则为零元素. T中每对对称边的符号(对应于符号模式矩阵P的一对对称的非主对角元素)为正，高度顶点集为H={1，2，3，4，5，6}.

将T转换为有向二部图为G(U，V)

根据算法1的第一步：仅含有一个高度点的团树为T₁₁，T₁₂和T₁₃，且H₁={1，4，6}. T₁₁，T₁₂和T₁₃所对应的有向二部图分别为G₁₁(U₁₁，V₁₁)，G₁₂(U₁₂，V₁₂)和G₁₃(U₁₃，V₁₃).在G₁₁(U₁₁，V₁₁)中有一个e圈为1-7′-7-1′-1，T中顶点1与顶点10又构成一个e圈1-10′-10-1′-1.由此，删除顶点1.在G₁₂(U₁₂，V₁₂)中有一个e圈为4-12′-12-15′-15-4′-4和另一个e圈为12-13′-13-12′-12.由此，删除顶点4和顶点13′.在G₁₃(U₁₃，V₁₃)中，在不同的完美匹配(6-17′，17-6′)，(6-18′，18-6′)，(6-19′，19-6′)和(20-19′，19-20′)中各自对应于一个e圈，分别为6-17′-17-6′-6，6-18′-18-6′-6，6-19′-19-6′-6和20-19′-19-20′-20.因此，删除顶点6与顶点20′.

当删除这些顶点后，则R₁={1，4，6}，L₁={13′，20′}，得到新的团树为T₁，它所对应的符号模式矩阵为

根据算法1的第二步，在T₁中，高度顶点集为H₂={2}.设对应的团树为T₂₁，将T₂₁转换为有向二部图G₂₁(U₂₁，V₂₁)，在G₂₁(U₂₁，V₂₁)中不含有e圈和孤立点，则P₁是非奇异的.则R₂=ϕ，L₂=ϕ.

由第一步和第二步得R={1，4，6}，L={13′，20′}.

在G(U，V)中，删除R和L后，得到有向二部图G′(U′，V′).在G′(U′，V′)中，既无孤立点，也无相同的“内邻居”点(或“外邻居”点)的顶点，则与G′(U′，V′)所对应的符号模式矩阵P′为非奇异的矩阵.则k=3，mr(T)=20-3=17.

例2  计算图 2中非对称符号树T的最小秩.

解：T中每个顶点处的符号(与之对应的符号模式矩阵P的主对角元素)如图 2所示，若无符号显示，则为零元素. T中每条边的符号(与之对应的符号模式矩阵P的非主对角元素)在图中已标识，高度顶点集为H={1，2，3，4，5，6}.

根据算法1的第一步，仅含有一个高度点的团树为T₁₁，T₁₂和T₁₃，且H₁={1，4，6}. T₁₁，T₁₂和T₁₃转换后的有向二部图分别为G₁₁(U₁₁，V₁₁)，G₁₂(U₁₂，V₁₂)和G₁₃(U₁₃，V₁₃).在G₁₁(U₁₁，V₁₁)中无e圈，但T₁₁的顶点1与其相邻团树的顶点10构成e圈1-10′-10-1′-1，由此，删除顶点1.在G₁₂(U₁₂，V₁₂)中，不同的匹配4-14′，14-4′和12-13′，13-12′所对应的e圈分别为4-14′-14-4′-4和12-13′-13-12′-12.另外，T₁₂的顶点4与其相邻团树的顶点3构成e圈4-3′-3-4′-4，由此，将顶点4和13′删除.在G₁₃(U₁₃，V₁₃)中，在不同的完美匹配(6-17′，17-6′)，(6-18′，18-6′)，(6-19′，19-6′)和(20-19′，19-20′)中各自对应于一个e圈分别为6-17′-17-6′-6，6-18′-18-6′-6，6-19′-19-6′-6和20-19′-19-20′-20.另外，T₁₃的顶点6与其相邻团树的顶点5构成e圈6-5′-5-6′-6.因此，删除顶点6与顶点19′.

由算法1第一步，G(U，V)中被删除的顶点集为R₁={1，4，6}，L₁={13′，19′}，得到新的团树T₁，T₁所对应的符号模式矩阵设为：

根据算法1的第二步，在T₁中，H₂={2}.设对应的团树为T₂₁，转换后的有向二部图为G₂₁(U₂₁，V₂₁).在G₂₁(U₂₁，V₂₁)中，不同的完美匹配(2-3′，3-2′)，(2-10′，10-2′)，(2-5′，5-2′)，(3-11′，11-3′)和(5-16′，16-5′)中各自对应于一个e圈分别为2-3′-3-2′-2，2-10′-10-2′-2，2-5′-5-2′-2，3-11′-11-3′-3，5-16′-16-5′-5，将顶点2，11′和16′删除.

由算法1第二步，G(U，V)中被删除的顶点集为R₂={2}，L₁={11′，16′}.得到新的团树为T₂，T₂中无高度点.

由第一步和第二步得R={1，2，4，6}，L={11′，13′，19′，20′}.在G(U，V)中，删除R和L后，得到有向二部图G′(U′，V′).在G′(U′，V′)中，不含有不相交的M-交替e圈.既无孤立点，也无相同的“内邻居”点(或“外邻居”点)的顶点，则与G′(U′，V′)所对应的符号模式矩阵P′为非奇异的矩阵.因此，mr(T)=20-4=16.