图 1鼓式制动器简化图制动器在工作时，制动鼓与制动蹄滑动接触产生制动摩擦力^[10].当制动器结构或材料设计不合理时会出现如尖叫噪声等各种不稳定现象，分析其原因，可以将制动鼓、制动蹄以及摩擦衬片离散化，将接触单元简化成四自由度的振动系统，如图 1所示.由于制动器属于小阻尼系统，可以忽略系统阻尼.因此，接触单元振动方程如式1所示.

其中，k_n为简化的弹簧单元刚度；x_d，s和x_d，r分别表示制动鼓表面第n个单元质心处切向t和径向r方向的位移，x_s，t和x_s，r则分别表示与之相对应制动蹄单元质心处t和r方向的位移.

若μ=0，即摩擦力为0，刚度矩阵[K]是关于k_n的对称矩阵；若μ≠0不对称，影响了其正定性，无法直接解耦，只能采用复模态解耦，通过子空间投影法，提取其复特征值.第i阶特征值可表示为

式中，α_i为实部，是系统的阻尼系数；ω_i为虚部，是系统的固有频率.与之对应的系统响应为

若α_i为负数，振幅A_ie^α_it随时间衰减，系统是稳定的，若α_i大于0，振幅则随时间不断增大.根据振动与噪声的关系，振动幅值越大，辐射声波的声压越大，声压级则越大，越容易产生制动尖叫现象.式(4)定义的不稳定性系数(Tendency of Instability，TOI)则表征了系统的不稳定程度，用T_TOI表示.

从式(4)可知，不稳定模态数目越多或实部数值越大，则T_TOI值越大，系统就变小为越不稳定，制动尖叫就越容易发生.

根据式(1)，刚度矩阵[K]的不对称是导致系统不稳定性的根本原因，它与摩擦系数μ和简化的弹簧单元刚度k_n的关系为式(5).

其中，k_dn，k_sn，k_ln分别为制动鼓、制动蹄和摩擦衬片的等效刚度，三者的等效刚度无法直接在模型中表达，而弹性模量可以度量刚度.因而，k_n大小与制动鼓、制动蹄和摩擦衬片的弹性模量有关.

系统总刚度矩阵中，k_n数量与接触单元数目有关，而接触单元又与接触面积有关.

综上所述，影响鼓式制动器不稳定性的因素有：摩擦系数、制动鼓、制动蹄和摩擦衬片的弹性模量，以及接触面积.

为研究鼓式制动器的摩擦接触导致的不稳定性，将模型简化为仅有制动鼓、制动蹄和摩擦衬片.采用Hypermesh划分网格，网格模型如图 2所示，共计23 612个单元，38 509个节点.

将网格模型导入ABAQUS软件中，对网格模型进行前处理.包括材料属性、接触设置、几何约束、载荷.具体如下：

1) 材料属性：参数如表 1所示.

2) 接触设置：定义制动蹄和摩擦衬片为面面绑定接触，二者无相对位移；摩擦衬片和制动鼓为面面滑动摩擦接触，接触约束采用罚函数法，引入罚参数α，采用虚位移原理求解出各接触点的接触力

式中${u_1} - {u_2} + \overline g $为两接触点间的距离，可以类比在物体间施加非线性弹簧.

3) 几何约束：制动鼓除绕z轴转动外其余自由度均约束；制动蹄下端除绕z轴转动、沿y轴移动外，其余自由度都要约束.

4) 载荷：制动蹄与活塞接触面上的制动压力用节点集中力代替.

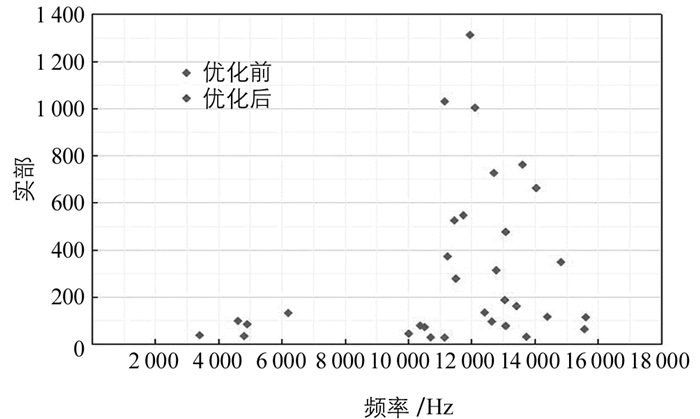
采用非对称模态求解器对建立的非线性有限元模型进行求解，提取复模态，其频率范围为0~16 kHz.实部大于零的不稳定模态如图 3所示.横坐标为虚部，纵坐标为实部.

由图 3可知，不稳定模态主要集中在3 500，4 900，6 200，10 500，11 200，11 900，12 800，13 500，14 600 Hz左右的9个频率范围.

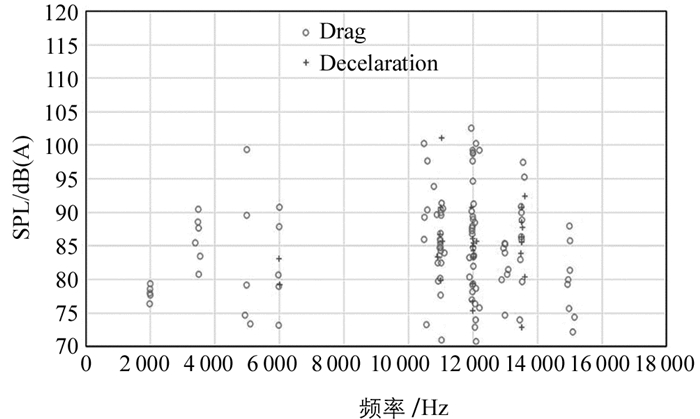
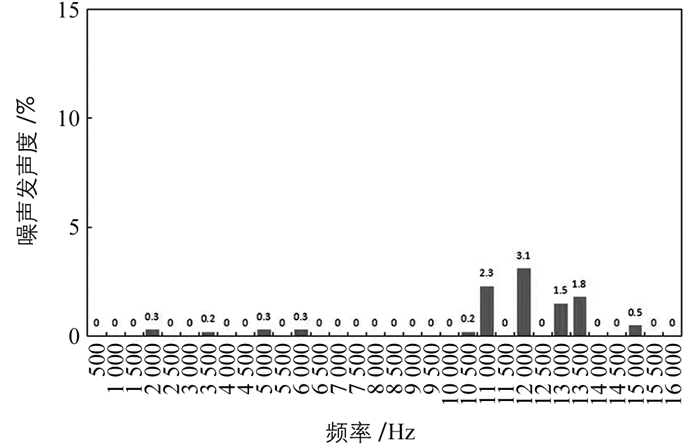
鼓式制动器NVH试验采用LMS公司的惯性制动试验台，按SAE J2521标准，试验工况为制动拖滞和减速制动工况.为减小环境噪声的影响，将制动器、悬架等放置在密闭空间，记录声压级大于70 dB的噪声发生度，结果如图 4和图 5所示.

由图 4和图 5可知，噪声发生频率基本包括不稳定模态频率，各频率下的发生度与不稳定模态实部的大小对应良好.与图 3比较发现，虽然仿真存在一定程度的低频欠预测，但其他频率范围的误差均不超过5%，说明鼓式制动器摩擦接触非线性有限元模型是有效的.

分析鼓式制动器不稳定性影响因素时，应用非线性有限元模型，考察模型的摩擦系数、材料弹性模量、接触面积等单一因素对制动不稳定性的影响.

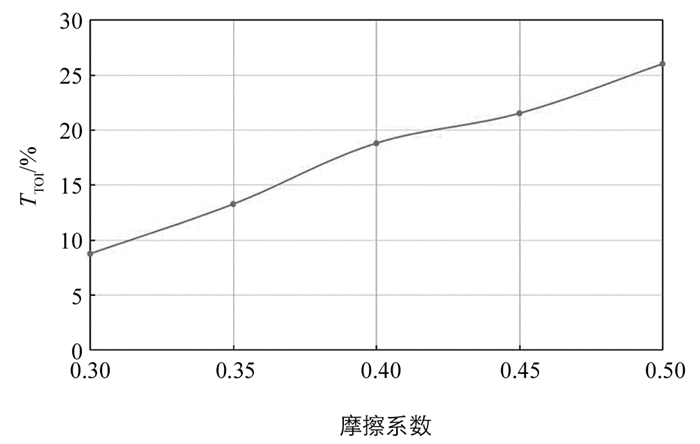
制动尖叫发生的最主要原因是制动鼓和制动蹄间耦合了摩擦力所致，对制动尖叫影响最大的因素就是摩擦系数.首先，将摩擦系数设置为0，仿真结果表明，制动器不存在不稳定模态.摩擦系数在0.3~0.5范围内时的制动器不稳定性系数如图 6所示.由图 6可知，随着摩擦系数的增加，不稳定性系数明显增加，越容易产生制动尖叫.

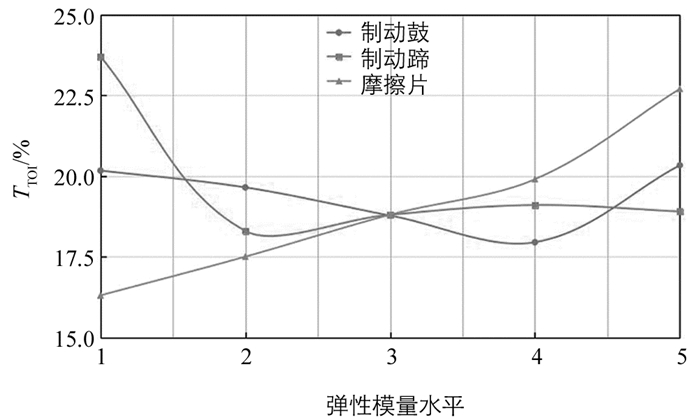
制动器在工作过程中会产生热量，弹性模量在温度的影响下会发生变化.根据制动鼓、制动蹄和摩擦衬片的材料特性，将其分别设置为5个水平(表 2)，研究各水平下制动器的不稳定性，结果如图 7所示.

由图 7可知，制动鼓、制动蹄和摩擦衬片的弹性模量对制动器不稳定性的影响各不相同，不稳定性系数随弹性模量的增加为非线性变化，其中摩擦衬片为基本正相关，其余不明显.

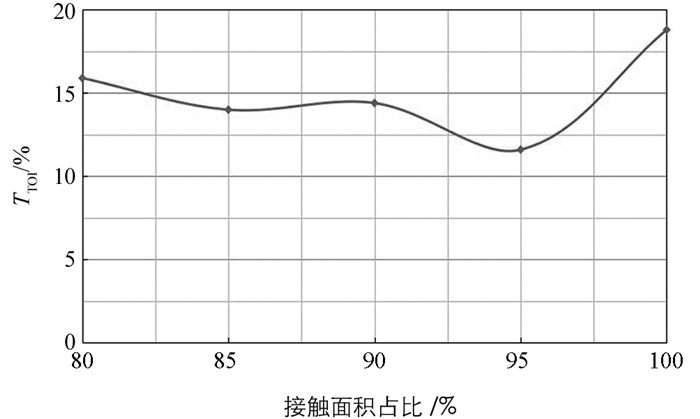
从节约材料和确保制动安全性能考虑^[11]，将摩擦片中间开槽，减小与制动鼓的接触面积，接触面积对制动器不稳定性的影响如图 8所示.

从图 8可知，开槽后的接触面积与开槽前的接触面积比值(接触面积占比)减小，不稳定性系数的变化规律不明显，但均比原模型的不稳定性有所改善，说明开槽有利于改善不稳定性.

基于制动器不稳定性的单因素影响分析，选取各影响因素为变量，不稳定性系数为目标，进行响应面设计.各因素水平如表 3所示，试验方案共有46组.拟合的回归方程为式(6).

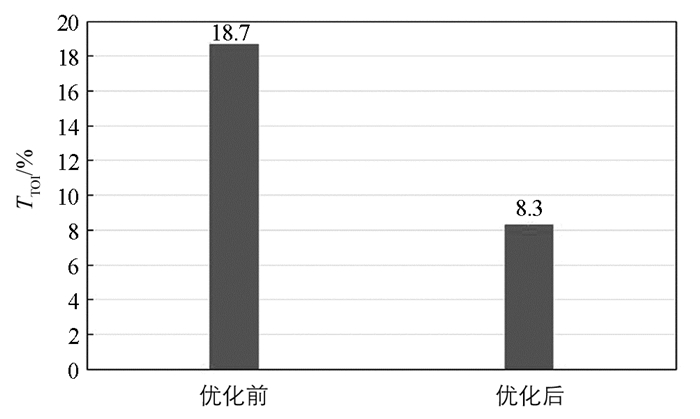
根据制动性能要求^[12-13]，摩擦系数不能小于0.35，接触面积占比不能小于0.9，经响应面法得到的优化方案是摩擦系数为0.35、接触面积为总面积的90%，制动鼓、制动蹄和摩擦衬片的弹性模量分别为1.33 GPa，2.31 GPa，369 MPa.优化前后制动器的不稳定性比较如图 9和10所示.

由图 9和图 10可知，制动器经优化后，其不稳定模态明显减少，不稳定性系数下降了55.6%，产生制动尖叫的倾向性明显下降.制动器设计部门可据此对其制动噪声进行改善.

从理论上分析了制动器不稳定性与制动尖叫的关系，总结了不稳定性的主要影响因素，应用有限元方法构建了鼓式制动器摩擦接触非线性有限元模型，并通过制动器NVH试验台架验证了模型的有效性，分析了各参数对不稳定性的影响，结论如下：

1) 理论分析和有限元仿真表明，制动器的不稳定性是摩擦耦合所致，基于摩擦接触的非线性有限元方法仿真研究有效.

2) 摩擦系数、弹性模量和接触面积对鼓式制动器不稳定性的影响较大，且为非线性的，其中摩擦衬片为基本正相关.

3) 制动器不稳定模态分布较广，实部数值较大，模态稳定性差，响应面优化改进相关参数后的不稳定性有明显改善.