-
IS-LM模型最早由希克斯提出,然后通过汉森的完善和推行,成为了较为完好的IS-LM模型.汉森在1949年提出简单的凯恩斯主义国民收入决定模型.这个模型经由萨缪尔森改进之后,形成了汉森-萨缪尔森模型,即汉森-萨缪尔森交叉图.曲线IS表述了商品市场均衡条件下,利率与产出关系的组合,曲线LM表明货币市场供需均衡条件下利率与收入关系的组合.在此基础上,经新古典综合派的共同努力,最终形成了完整的IS-LM模型.在证实了凯恩斯的国民收入决定理论正确性的同时,也在理论和方法上发展了凯恩斯学说.然而IS-LM模型中并没有对外贸易和外资方面的触及,也即该模型基本是针对封闭式经济体系的论述.在考虑对外贸易和外资等因素并加入国际收支均衡曲线(即BP曲线)后,该模型逐渐发展成为IS-LM-BP模型,它是开放经济条件下国内外经济均衡的重要经济模型之一[1-8].文献[9]探讨了动态IS-LM模型的宏观经济政策设计,设计了该模型的一个纯增益反馈控制器,并得到了可任意极点配置的闭环系统.将反馈控制器的设计方法应用到不同的经济模型当中,以达到系统的稳定[10-13],具有非常重要的意义.
本文参考文献[9]的设计方法,对文献[4]引入的IS-LM-BP模型进行反馈控制,在文献[4]的基础上,将其反馈控制的方式系统化.文献[4]对模型进行分析并对模型中的参数赋值,在参数确定的模型基础上,通过反馈控制得到一个数值确定的反馈矩阵.而本文则设计了一种纯增益反馈控制器,在参数未给定的前提下,通过反馈控制的方法得到了一个含参数的反馈矩阵.针对参数不确定的IS-LM-BP模型,对于不同的参数取值,可直接得到反馈矩阵,并利用所设计的反馈控制器使实际总供给趋于计划总供给、实际汇率趋于计划汇率.该反馈控制方法在不改变系统的能达性的前提下,使得不稳定的开环系统在选取适当的增益矩阵后,对应的闭环系统达到渐近稳定,并且能够对输出进行调节.
全文HTML
-
考虑到实际情况下,中国短期汇率相对稳定,给出了如下包括企业、消费者、政府和对外经济部门在内的经济模型.
-
在开放经济条件下的总需求或国民总收入恒等式变为:
其中:C(t)为消费需求,I(t)为投资需求,G(t)为政府支出需求,NX(t)为净出口需求.
投资需求方程为:
其中r(t)为第t个时间周期的利率水平.而投资水平依赖于收入水平,利率与投资需求量成反比.为简化,用下面的线性方程来表述式(2)各项相互间的关系[16]:
其中a,b>0.
消费与国民总收入的关系为:
其中:u>0为税率,是税收总量占国民总收入的总比重;α>0为自发消费部分;β>0为边际消费倾向.
宏观经济学将汇率和国内收入水平列为两个最重要的影响净出口的因素,因而净出口函数常被简化地表示为[1]:
其中:q,γ,n>0,γ为边际进口倾向;E是名义汇率;P和Pf分别为国内和国外价格指数.
将式(3),(4),(5)带入到收入恒等式(1)中,有:
即为所得IS曲线的方程,该曲线表示现行汇率下,总支出与总收入相等时,利率和收入水平的组合.
-
开放经济条件下,货币的总需求是民众对货币的预防动机、交易需求和投机需求的总和.汇率影响货币需求的可能性比较小,收入与货币的交易需求成正比,而利率与投机需求成反比.因此货币的总需求函数可表述为:
其中M,m和P分别表示名义货币量、实际货币量和价格指数,则货币供给量方程可描述为:
利率调节方程[16]:
其中ε>0为利率调节系数.当货币供给m(t)小于货币需求L(t)时,第t+1个时间周期利率r(t+1)上升.反之,下降.
综合货币总需求、总供给及利率调节方程,可得到开放经济条件下,货币市场的均衡方程:
即为所得LM曲线的方程,该曲线描述了开放经济条件下,货币需求与供给相等时利率和收入水平的组合.
-
在开放经济中,如果国外利率低于本国利率,外国的投资和贷款就会流入本国导致净资本流出的减少[4],反之增加.一般而言,净资本流出由本国与外国利率差额的函数来表示,且常用线性函数,则净资本流出函数为
其中:rω表示外国利率,r(t)表示本国利率,σ>0为常数.
国际收支差额体现为净出口和净资本流出的差额,用BP表示,则有:
在宏观经济学中,将一个国家的国际收支差额为0定义为外部均衡,即BP=0.那么当国际收支平衡时,则有
将式(5)和式(11)代入式(13)可得:
即为BP曲线方程,该曲线表示在给定汇率下,国际收支相一致时,利率和收入的组合.
1.1. 开放经济条件下的IS曲线方程
1.2. 开放经济中的LM曲线方程
1.3. 开放经济中的BP曲线方程
-
系统模型给出之后,首先分析系统的状态变量与目标即输出变量.在本系统中将r,Y和实际汇率
$\frac{{E{P_f}}}{P}$ 作为状态变量.一个国家期望一定时期内实际国民总收入增长率基本保持不变,同时也期望利率波动较小.因而将系统要控制的量设为输出变量:其中:i*,Y0*是计划利率和计划总供给,δ为经济增长率,i*,Y0*,δ均为给定常数.
状态变量与输出变量确定后,接下来确定系统的控制变量.在本系统中,可令政府支出G(t)与货币供给量M(t)为控制变量,它们通常被称为财政政策变量与货币政策变量[5].由于第一部分所得的IS-LM-BP模型是离散时间经济系统,故而需要将模型转换成状态空间模型.
由方程(7)-(9)可得
由方程(10)与(15)可得
令
由方程式(6),式(14)与式(16)可得
将上述系统状态方程写成矩阵形式,令状态向量
输入变量
扰动项
其中
系统中假定国外利率水平固定,为常数rω,并入扰动项.则IS-LM-BP模型的动态系统方程可表示为:
系统输出方程表示为:
扰动方程表示为:
式(18),(19),(20)中各个矩阵为:
其中:
-
对于离散时间定常线性系统
如果该系统不稳定,即A的特征值不全在复平面单位圆内,通过反馈控制选取适当的纯增益反馈控制器,能够使该系统所对应的闭环系统渐近稳定,并达到输出调节.在IS-LM-BP模型中,对参数的不同取值使得系统的稳定性无法保证,通过状态反馈使闭环系统具有事先指定的极点,并调节实际总供给和实际利率,从而达到计划的目标.
引理1(极点配置定理)[9] 离散时间定常线性系统x(t+1)=Ax(t)+Bu(t)能够任意配置极点的充分必要条件是该系统是完全能达的,即
引理2[4] 给定离散时间系统x(t+1)=Ax(t)+Bu(t)+Eω(t),并假设(A,B)完全能达,则该系统存在纯增益反馈控制器u(t)=K1x(t)+K2ω(t),使闭环系统渐近稳定并达到输出调节的充分必要条件是存在矩阵U和V满足矩阵方程
根据引理1,系统(18)完全能达的充分必要条件是rank(B,BA,…,Bn-1A)=n,此时n=3,而
由此可知
从而系统能达.
设
求解矩阵方程
由D=02×3,则
结合矩阵方程组中的第一个矩阵方程,可知矩阵U并不唯一,不妨令u31=1,u32=u33=u34=u35=0,可求得
其中
即存在满足矩阵方程(21)的矩阵U和V,由此可给出如下结论:
定理1 当系统(18)完全能达,且存在矩阵U和V满足矩阵方程(21)时,该系统存在纯增益反馈控制器
使闭环系统
渐近稳定,并达到输出调节,即有
证 由引理1及引理2分析可知,系统(18)完全能达并且存在满足矩阵方程(21)的矩阵U和V,因此设该纯增益反馈控制器为
该系统可极点任意配置,若使闭环系统的极点全在复平面的单位圆内,则闭环系统渐近稳定.
观察所得矩阵Ac,存在矩阵K1,当k13=k21=k23=k31=k32=0,
${k_{12}} = \frac{P}{\varepsilon } - hP$ ,${k_{33}} = \frac{{\rho h\varepsilon n}}{\gamma }$ 时,若要求的闭环极点为λ1,λ2,λ3,λi<1,i=1,2,3,则
由此可知矩阵Ac的特征方程为
其中
可得
其中
根据纯增益反馈控制器设计原理,可由K1得到
计算可得
其中
至此,得到系统(18)的一个反馈控制器.在复平面单位圆内任意选取的极点均能保证在该控制器下闭环系统渐近稳定;接下来根据所得控制器验证系统是否能够达到输出调节.
将K1,K2代入式(22),并结合式(15),(16)可得
由此得,
又由于
由|λ2|<1,|λ3|<1,可得
从而
且有
从而
若极限存在,令
a为任意常数,则有
$a = \frac{1}{{kP}}{k_{22}} \cdot a$ 即$\left( {1 - \frac{1}{{kP}}{k_{22}}} \right) \cdot a = 0$ ,由k22的任意性可知a=0,因而闭环系统达到输出调节,即有
-
对该模型的宏观经济政策进行分析,将所得反馈增益矩阵K1,K2代入式(22),得到的纯增益反馈控制器为:
将k11,k22代入(24)式可得
由
知
于是,由方程(25)前两式可知,货币供给的调节机制是,在实际总供给与实际利率的基础上,与实际利率偏离计划利率之差额r(t)-i*同向发生变化,与实际总供给偏离计划总供给之差额Y(t)-Yt*反方向变化,与计划总供给Yt*同方向变化,与计划利率i*反方向变化.由式(26)知,政府支出Gt的调节机制是在实际汇率的基础上,计划利率和计划总供给的关系由系数v34,v35决定,即:若v34>0则与i*反方向变化,反之,同向变化;若v35>0则与Yt*反方向变化,反之,同向变化.
-
为验证第3部分所得纯增益反馈控制器的调节效果,我们参照文献[4]的一组参数值,并结合Matlab软件进行数值模拟. ε为利率调节系数,反映了货币需求与货币供给不均衡时利率的变化,一般取值为较小的正数,故我们取ε=0.05;k为货币总需求的调节系数,反映了总供给与货币总需求间的比例关系,取k=0.1;价格指数P反映的是不同时期一组商品(服务项目)价格水平的变化方向、趋势和程度,我们期望价格处于稳定的状态,因而取P=1;r0和Y0分别表示了利率与总供给的初值,取值分别为r0=0.2,Y0=30.25,i*和Y0*则是我们计划达到的利率与总供给并取值i*=0.15,Y0*=30(表 1).
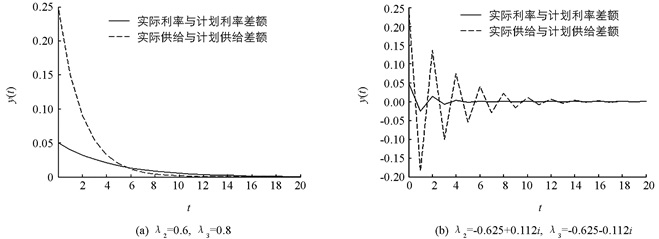
对任意的极点λ2,λ3|λ2|<1,|λ3|<1,进行纯增益反馈控制器的设计,仿真结果见图 1.
从图 1可以看到,在同一组参数之下,对不同的期望的极点,随时间推移,系统总能够达到输出调节,而经过反馈控制的系统,极点的选取保证了闭环系统是渐近稳定的.
-
本文主要对IS-LM-BP模型进行了宏观政策设计,以国民总收入Y(t)、利率r(t)与实际汇率
$\frac{{E{P_f}}}{P}\left( t \right)$ 为状态向量,第t期的名义货币量M(t)、第t+1期的名义货币量M(t+1)及第t+1期的政府支出需求G(t+1)为控制输入变量,以实际利率与计划利率的差额r(t)-i*和实际总供给与计划总供给的差额Y(t)-Yt*为输出向量,设计了一个纯增益反馈控制器,使得IS-LM-BP系统能够实现复平面单位圆内任意极点的配置,并且达到输出平衡.根据数值模拟的结果可以看到,随着时间的推移,输出量趋于0,即实际利率和总供给趋于计划利率和总供给.本文的宏观政策设计方法相较于文献[4],其创新点体现在反馈控制方式上的系统化.本文中由模型所得的含参数反馈矩阵对给定的不同的参数取值,能够直接得到不同的反馈控制器u(t)=K1x(t)+K2ω(t),而根据计算得到的含参数反馈矩阵也不唯一.根据数值模拟的结果,表明本文所选取的反馈控制器能够对IS-LM-BP模型进行控制,使得系统渐近稳定并达到输出调节.本文没有考虑实际情况下宏观政策的延迟因素,因此有必要加入更多的政策工具以实现经济的宏观调控,且在实际情况下,各变量之间的关系复杂,本文只考虑了线性关系忽略了变量间的非线性关系,所涉及的非线性控制问题有待于我们进一步研究.



 下载:
下载: