-
随着城市机动车数量的增长,交通拥堵和城市停车难问题越来越严重,传统的停车场已经无法满足停车需求,受此影响,自动化立体车库应运而生.自动化立体车库具有容量大、节约空间、自动化程度高等优点,为保证立体车库具有较高的运行效率,提高顾客满意度,在对立体车库进行设计时需考虑整体车库库位层列布局和设备服务资源配置.
以往文献主要针对库位分区、调度策略等问题进行研究分析.如刘日等人[1]以多色集为理论依据,对立体车库进行了库位分区,与就近库位分配进库方式下顾客等待时间和等待能耗进行了对比,并对车辆停留时间范围进行了预测.王小农等人[2]针对自动化立体车库车位分配时顾客排队过长以及堆垛机能耗过高等问题,提出了采用两阶段混合算法对车位进行分配.王丽杰等人[3]研究了巷道堆垛式立体车库车辆传送策略及智能测控方法.左为恒等人[4]提出了一种根据车辆到达率的变化,采用调度堆垛机数量和运行速度相结合的新调度策略.而针对自动化立体车库调度算法的研究分析,吕洪柱等人[5]设计了一种智能存取车控制算法,对车位编号采用效益优先排序算法,实现了经济效益最优.李建国等人[6-7]提出了一种基于遗传算法的堆垛机路径优化方案.张华庆[8]等人建立了车辆路径问题的数学模型,并采用改进遗传算法对路径进行优化.文献[9-11]对自动存取系统(Automated Storage/Retrieval System,AS/RS)进行了分析研究,分别就搬运器与堆垛机的动态作业问题、堆垛机与搬运器的组合数量问题等进行了分析.
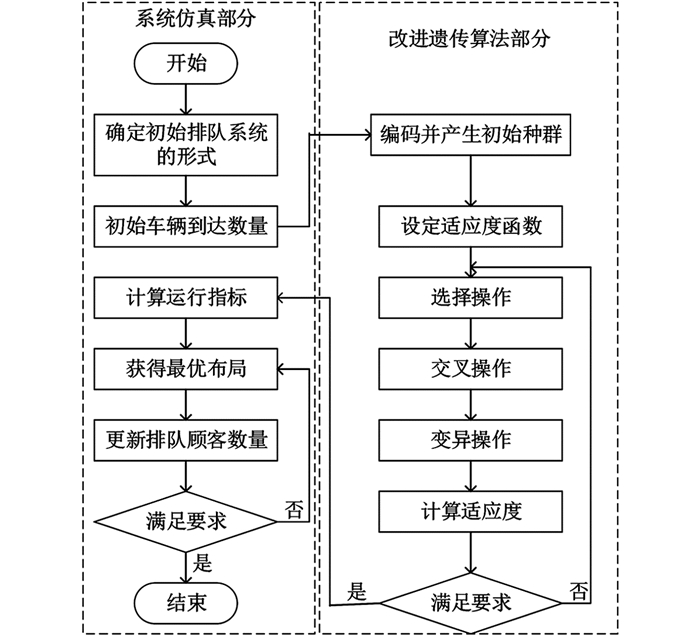
目前,针对自动化立体车库的研究主要集中在库位分区、运行效率等,而缺少根据实际运行的车库进行排队分析,不同的排队系统下不同库位层列布局、服务资源配置的立体车库运行效率存在较大差异.而改进遗传算法通过改进编码、交叉、变异等自身环节,在对堆垛机进行调度时能够很好地选择最优路径从而缩短运行时间.本研究根据前人思想及排队论基本原理,以堆垛机库内运行时间和顾客库外等待队长为目标对象,考虑车库层列不同组合以及服务资源配置数量对顾客平均等待时间和平均等待队长的影响,再利用改进遗传算法对堆垛机的运行进行优化,使堆垛机在库内运行时间最短,缩短顾客等待时间和等待队长,一方面减少立体车库能耗,降低运营成本,另一方面提高顾客满意度.
HTML
-
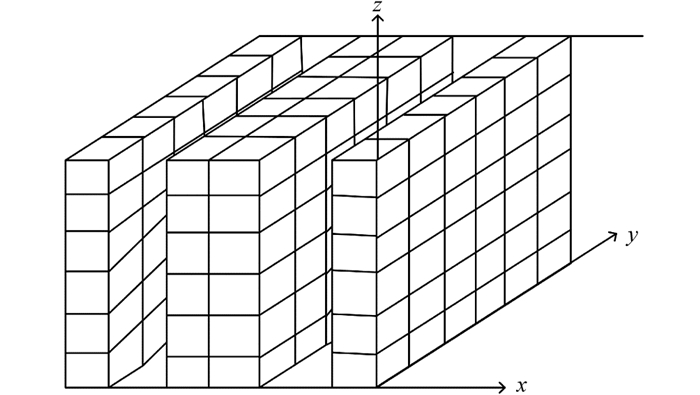
巷道堆垛式立体车库主要由车厅、巷道、停车位、堆垛机和搬运器等组成,可以根据场地和高度的不同要求建成多种结构形式[12].立体车库本身是三维实体[13],本文将堆垛机选择巷道的操作方向定为x轴方向,将堆垛机选择所要进行存取操作列的方向定为y轴方向,将选择所在层的操作方向定为z轴方向.巷道堆垛式立体车库库位模型如图 1所示.
由于存取车作业是三维运动[14],即在巷道内所进行一次存取车操作可分解为3个分方向上的运动—巷道方向上的水平运动(x),用来选择巷道,并实现存取操作;垂直方向(z)升降运动,即存取车位点所在的层j,用来选择车位所处的层;横向(y)存取运动,即存取车位点所在的列i.对于不同的车位而言,x方向上的操作相同,因此可将模型简化为单巷道内(y,z)的二维运动,即寻找存取车位点(i,j).由立体车库简化成的单巷道实体模型进行分析,将立体车库模型简化,取I/O口位置为坐标原点O,取选择存取位置所在列的方向为i轴,取选择存取位置所在层的方向为j轴,取单侧车位进行分析,单侧平面图如图 2所示.
-
一个完整的排队系统主要由输入过程、服务机构、排队规则3个部分组成[15],排队系统示意图如图 3所示.研究排队问题的目的是研究排队系统的运行效率,估计服务质量,确定系统参数的最优值,以决定系统的结构是否合理,设计改进措施等.
停车位排队过程可以描述为当车辆按照一定的概率到达车厅后,如果车库的停车位已满,则直接离去,如果有停车位,则进入服务台排队系统.由于立体车库车厅容量有限,不能无限制地容纳排队等待的车辆,当车辆进入立体车库车厅后,若排队车辆数大于车厅排队系统容量,则车辆直接离去,否则排队等待.
综上分析可知,可将立体车库停车位排队过程看成是一个排队系统容量有限型的多服务台混合损失制排队模型M/M/S/C/N/∞.
-
《车库建筑设计规范(2015)》规定,1个I/O口对应约50个停车位,I/O口处应设置不少于2个的候车位,I/O口分开设置时,候车位不应少于1个.考虑立体车库造价等问题,立体车库的最低层数为3层.堆垛机水平速度v1=80 m/min;堆垛机垂直速度v2=20 m/min;车库车位的长L0=5 m,宽W0=2 m,高H0=1.8 m,但是规范中明显缺少了对库位如何进行布局的规定.
在车库排队系统中,其运行参考指标主要包括[16]:
① 顾客的到达率服从参数为λ的泊松分布,服务时间服从参数为μ的负指数分布;
② 整个车库系统中的顾客平均等待队长Lq和等待时间Wq;
③ 堆垛机数量s对顾客必须排队等待的概率ps和平均等待时间Wq的影响.
自动化立体车库有一个排队队列,有s个堆垛机参与存取任务,而且各个堆垛机之间相互独立,定义服务强度ρs=λ/(sμ).系统内有C个服务台,如果车库内车辆已满,最新到达的车辆将直接离去,则系统内必定有m-C个可供车辆排队的位置,即车库容量为m-C.当C个服务台都处于忙碌状态时,系统的总服务率为
则停车排队系统空闲概率P0为
其中,n表示排队系统中有n个堆垛机正在参与服务,且0≤n < s,0≤i<s.
服务台排队系统主要指标的计算公式为
车辆在系统内平均等待时间Wq′为:
在排队系统中,只有当准备接收服务的车辆大于堆垛机的数量s时,才会出现车辆排队等待,所以等待服务车辆的平均数Lq为
堆垛机空闲概率ps为:
设车库巷道数为D,车辆在从服务台运送到存放位置所需时间T均为
其中,j为停车位所在的层,i为停车位所在的列,i,j均为正整数.
则系统运行时顾客的平均等待时间Wq为:
其中,k表示停放车辆数,m表示车库停车位个数.
1.1. 巷道堆垛式立体车库实体模型
1.2. 巷道堆垛式立体车库排队模型
1.3. 立体车库系统模型建立
-
根据哈尔滨某自动化立体车库实际运行数据,车辆到达率服从参数为λ=0.5(辆/min)的泊松分布,车库服务率μ=0.9(辆/min),考虑每天即1 440 min内车库运行情况,考虑设计立体车库容量为320个,车库整体构造为双排对列布设,巷道数为2,服务台数为3,再考虑整个立体车库造价等问题,给出如表 1所示的不同层、列组合.
针对表 1中的11种不同层列组合情况,对排队系统容量N分别为5,10,25,50辆时,顾客的平均等待时间Wq、平均等待队长Lq和堆垛机空闲概率ps进行计算分析,考虑堆垛机数s为5台和6台,立体车库效能对比如表 2、表 3、表 4和表 5所示.
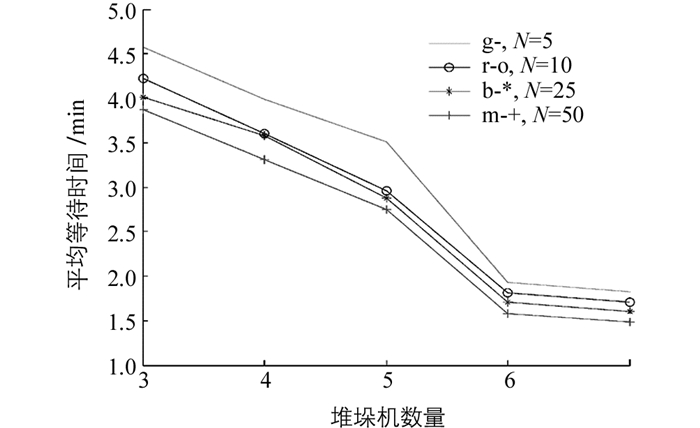
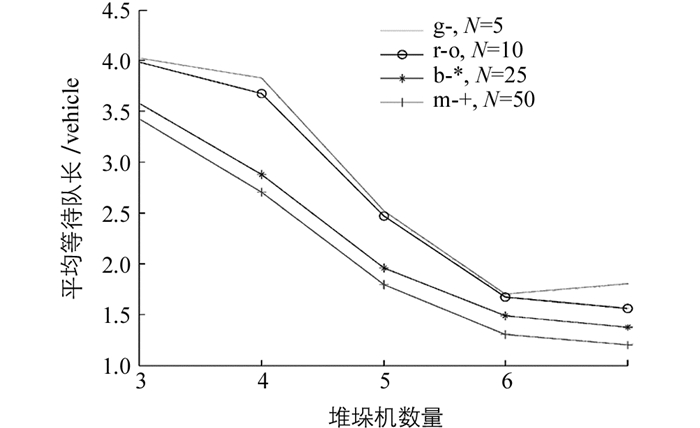
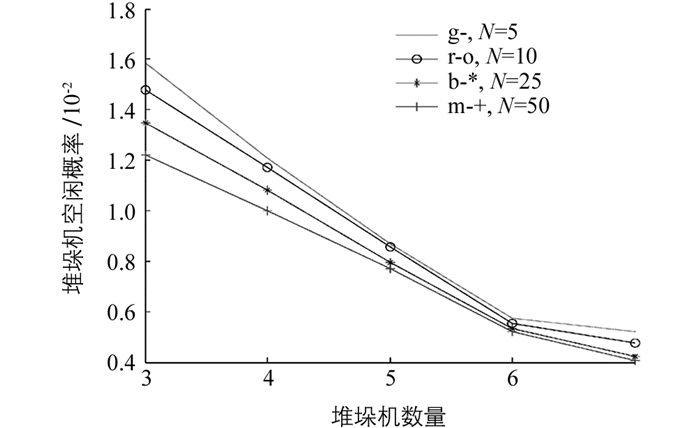
从表 2-表 5可以看出,S5情况即8层10列的库位布局下,衡量车库运行效率的3项指标均相对最优,且堆垛机数量为6台时比5台时,顾客的平均等待时间Wq缩短了约26%~30%、平均等待队长Lq缩短了约27%,堆垛机空闲概率ps下降了0.07%左右.堆垛机数量对各顾客的平均等待时间Wq、平均等待队长Lq和堆垛机空闲概率ps的影响如图 4、图 5和图 6所示.
从图 4和图 5可以看出,随着堆垛机数量的增加,各项指标值逐渐下降,并趋于一个稳定值,但是从图 6可以看出,随着堆垛机配置数量的增加,在堆垛机配置数量为6台时,堆垛机的运行效率最高,故得出结论:在堆垛机数量为6台时,车库各项运行指标相对最优.
-
传统的调度策略在对立体车库进行调度时,目标函数不明确,操作繁琐,效率低下,因此需要寻找一种高效合理的调度策略对立体车库进行模拟调度[17].遗传算法是一种全局优化算法,具有计算速度快、收敛性好、鲁棒性高等优点,这些特性已被人们广泛地应用于组合优化、自适应控制等领域.但是遗传算法实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码,因此本文针对遗传算法本身的特点进行改进,提出了一种改进的遗传算法对立体车库的调度进行优化.
-
1) 染色体编码
通常遗传算法采用二进制编码,但确定初始化排队系统后,顾客到达数量初始化后为大量浮点数,若采用二进制编码则导致位串过长,影响搜索效率,因此本文采用浮点数编码直接进行自然描述,无编码解码过程,以相对较小的长度实现足够大精度的要求,并随机产生初始种群.
2) 适应度函数[18]
适应度函数可对种群中每个个体进行估计,与性能的优良成正比,这里定义个体适应度函数为
式中,n为该个体所通过的库位数目总和,T为该个体中相邻序号库位间运行所需时间之和.
3) 交叉变异
采用Monte Carlo法选择算子[19],个体适应度越大,被选择的概率越高.设种群数量为m,个体n的适度值为F,则选中个体a的概率为
从父代里随机选择两个个体wr和wl随机独立地选连接值进行交换,其在b位的交叉操作为
其中β为[0, 1]间的随机数.
以某一较小概率完成均匀变异,使个体适应度更高,从局部角度逼近最优解.变异后的新基因值为
其中wmax,wmin分别为初始个体的最大和最小值,γ为[0, 1]间的随机数.
综上所述,通过选择、交叉、变异等操作,使个体不断地进化达到最优解,从而实现堆垛机运行效率的优化,使堆垛机在库内的运行时间最短,缩短顾客等待时间和排队队长.
-
考虑立体车库在8层10列6台堆垛机双排对列双巷道布局配置时,设定改进遗传算法种群数大小为350,最大迭代次数为350,变异概率pm=0.05,交叉概率pc=0.9,以堆垛机运行时间和顾客平均等待队长最短为目标对车库进行优化仿真.
在复合作业方式下,通过仿真得到5组符合实际运行的一天内随机存取车总数值:(317,288)、(306,253)、(296,244)、(267,207)、(281,234),由仿真模拟可知,排队系统容量N为25、50时,相对较优,因此在此处对排队系统容量N分别为25和50时,采用改进遗传算法对顾客平均等待时间Wq、平均等待队长Lq以及堆垛机空闲概率ps进行优化(表 6).
由表 6可以看出,以排队系统容量为50时为例,改进遗传算法优化效果更优,将改进遗传算法优化后的结果与蚁群算法、模拟退火算法进行对比,顾客平均等待时间Wq、平均等待队长Lq以及堆垛机空闲概率ps对比如表 7所示.
分析表 7中的数据可以看出,改进遗传算法在协调立体车库调度比蚁群算法和模拟退火算法都相对较优,其中顾客平均等待时间Wq缩短了约29.1%,平均等待队长Lq缩短了约47.8%以及堆垛机空闲概率ps降低了约0.31%.
实验仿真是在电脑配置为CPU Intel i7处理器,MATLAB-2014a运行环境下进行的.考虑各算法的复杂度,主要从时间复杂度和迭代次数两方面进行对比,如表 8所示.
从表 8可以看出,改进遗传算法无论在算法执行时间还是迭代次数上均优于其他两种算法,因此,采用改进遗传算法对立体车库调度分析具有一定的优越性.
对表 7和表 8中的数据进行分析,从仿真结果来看,采用改进遗传算法对立体车库整体进行调度优化,可以缩短顾客平均等待时间、平均等待队长,提高整体运行效率.
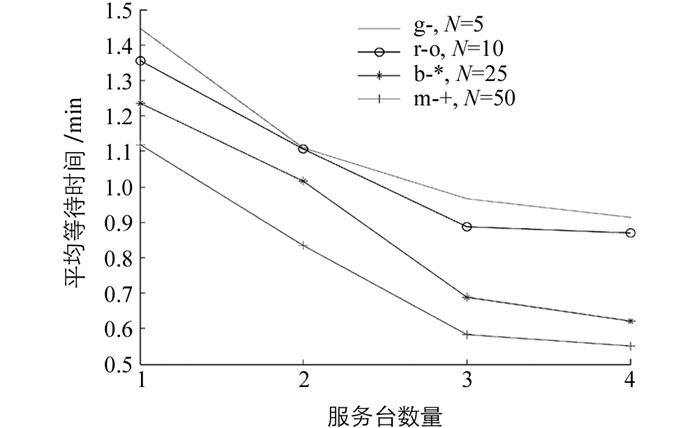
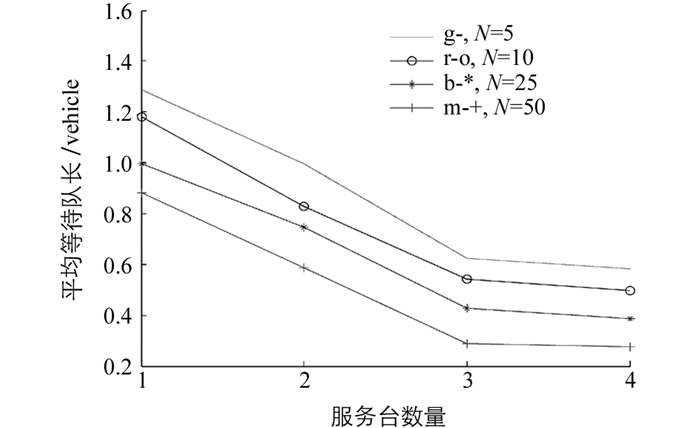
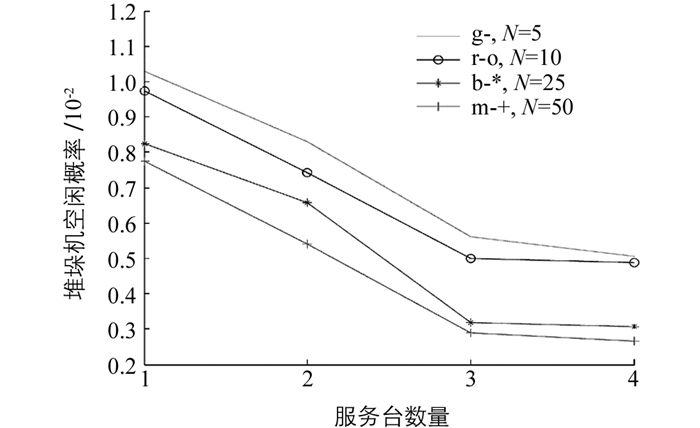
立体车库在8层10列、双巷道双排对列布设、堆垛机数量为6台、服务台数为3时,得到了较合理的结果.再综合考虑不同服务台数量对顾客平均等待时间Wq、平均等待队长Lq及堆垛机空闲概率ps的影响,如图 8-图 10所示.
分析图 8-图 10可以看出,在该排队系统下服务台数对顾客平均等待时间Wq、平均等待队长Lq及堆垛机空闲概率ps的影响较大,从图中可以看出服务台数量为3时,各项指标趋于最优.服务台数为3比服务台为2时平均等待时间Wq缩短了约30.3%,平均等待队长Lq缩短了约50.7%,堆垛机空闲概率ps缩短了约0.252%.
3.1. 改进遗传算法的实现
3.2. 仿真与分析
-
本文以巷道堆垛式自动化立体车库为研究对象,以排队理论为基础,分析了立体车库的排队模型,考虑了其层、列布局对立体车库整体运行效率的影响,并在运行效率较高库位布局下考虑了不同堆垛机数量、服务台数对运行效率的影响.
1) 通过对立体车库现场数据的采集和分析,并根据立体车库实际运行情况将立体车库停车位排队过程看成一个多服务台混合损失制排队模型M/M/S/C/N/∞.
2) 通过仿真实验得到立体车库在8层10列、双层队列布设、巷道数为2、堆垛机数为6台时,车库整体运行效率相对较高,并用改进遗传算法优化立体车库调度得出优化后的调度策略比采用模拟退火算法下顾客平均等待时间Wq缩短了约29.1%、平均等待队长Lq缩短了约47.8%以及堆垛机空闲概率ps降低了约0.31%,服务台数量为3时可以满足立体车库整体运行.
3) 从对立体车库的分析与仿真结果来看,得到了比较理想的结果,提高了立体车库库位利用率和堆垛机运行效率,降低了立体车库建设成本,为立体车库企业能带来一定的经济效益和社会效益,对立体车库的快速发展及广泛应用具有积极意义.








 DownLoad:
DownLoad: