-
电力作为一种特殊能源,无法实现大规模存储,因此,保持电力的供需平衡是至关重要的,供电过量会造成资源的浪费,供电不足则会导致经济损失,甚至影响社会稳定.我国建筑面积庞大,若是能够建立准确预测建筑用电负荷的模型,对于我国加快节能减排政策的落实将会有重大的意义.而如何提高用电负荷预测的准确率一直以来都是国内外学者研究的热点问题.
李婉华[1]以随机森林和极限学习机为基础,通过引入粒子群优化算法以及变异算子,改进了算法的泛化性能以及稳定性,提升了电力数据的预测性能;Fazil Kaytez[2]结合最小二乘支持向量机与自回归移动平均对土耳其的电力数据进行了预测,并将结果与其他模型进行比较,证明了模型的有效性;王月强等[3]提出了基于多时空的用电负荷预测模型,通过小波分解方法分解负荷数据的各时空分量,并对不同分量选择不同模型进行分析预测,大大提升了模型预测的精确度;魏华栋等[4]通过小波变换细化负荷数据的伸缩变换,并结合长短期记忆神经网络的梯度计算,有效提升了负荷预测结果的精度;罗澍忻等[5]提出了一种堆叠长短期记忆网络的模型,将不同时间尺度的历史负荷数据以及地区经济和气候数据导入模型,通过实验验证该模型提升了负荷预测的准确性;邢伟等[6]通过集合干扰重构经验模态分解算法将用电负荷数据分解为多个平稳分量,并提出了改进多尺度散布熵算法刻画原始用电数据的内在特征,从而提升了模型预测的准确性.
尽管用电负荷数据预测的研究很广泛,但仍存在以下几个问题:
1) 特征的选择不够深入.现有的预测研究方法没有深入分析用电负荷数据的影响因素,往往直接将影响因素作为输入进行预测,很大程度上影响了模型的预测精度.
2) 数据量要求大.目前的研究方法主要以神经网络为主,需要庞大的数据量进行训练,才能取得理想的预测精度,而我国的能源监测系统近年来才逐渐完善,针对单一建筑的用电负荷数据有限,很难获取如此大的数据量进行训练.
3) 对波动性强的用电负荷数据预测精度较差.现有的研究方法对于用电规律明显的数据预测精度较高,但当用电负荷数据波动性较大时,预测的精度显著下降.
针对以上问题,本文提出了一种基于时间序列多尺度分解的混合预测模型(EEMD-LSSVR-ARIMA模型).经研究发现,用电量与建筑面积、楼层高度以及各气象因素密切相关,而本次实验针对的是单一建筑,建筑面积与楼层高度固定,因此本次实验主要分析气象数据对用电量的影响,经综合考量,本文选择空气温度、露点温度、海平面气压作为影响因素,使用集合经验模态分解(EEMD)[7]分别将用电负荷数据和3种影响因素数据按其内在的时间尺度特征自适应地分解为多个本征模态分量,保证原始数据信息不丢失,在深入分析用电负荷数据分量与各影响因素分量之间关系的基础上,使用最小二乘支持向量回归(LSSVR)[8-9]模型和差分自回归移动平均(ARIMA)[10]模型分别对用电负荷数据的各分量进行预测,从而可以最大程度地拟合各分量数据,再将预测结果叠加,得到最后的预测结果.并通过实验分析验证模型的有效性.
HTML
-
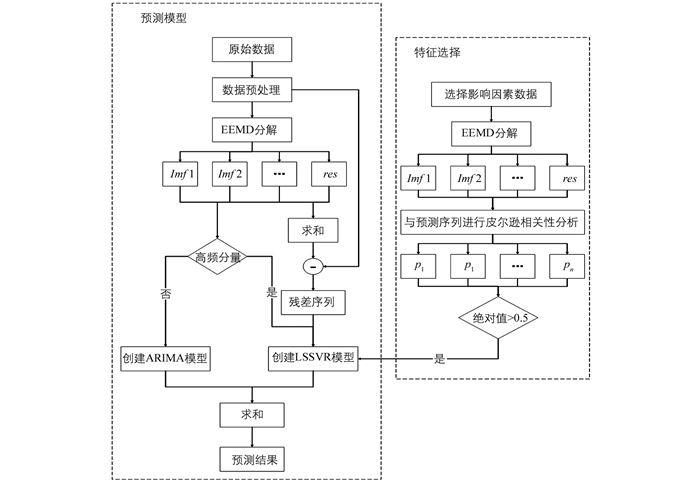
考虑到建筑用电负荷数据具有很强的波动性和非线性特征,本文提出了一种基于时间序列多尺度分解的EEMD-LSSVR-ARIMA混合预测模型对用电负荷数据进行预测,通过EEMD将数据分解为多个频率不同的分量,使用线性模型ARIMA预测低频分量,使用非线性模型LSSVR预测高频分量,充分发挥不同模型的预测性能,从而达到提升预测精度的目的.模型流程图如图 1所示.
模型设计思路如下:
1) 使用EEMD将预处理后的用电负荷数据分解为多个本征模态分量;
2) 计算原数据序列与经EEMD分解后的各分量之和的差值,得到差值序列;
3) 选择影响用电负荷数据因素,使用EEMD分解影响因素序列,分解为多个频率不同的分量;
4) 使用LSSVR预测用电负荷数据的高频分量和差值序列.通过皮尔逊关联分析法分析影响因素数据的各分量序列与要预测的数据序列的相关性,选择相关系数绝对值大于0.5的分量作为LSSVR模型的输入数据,输出要预测的数据;
5) 使用ARIMA模型预测用电负荷数据中的低频分量;
6) 将各分量预测结果和差值序列预测结果等权值求和,得到最终的预测结果.
-
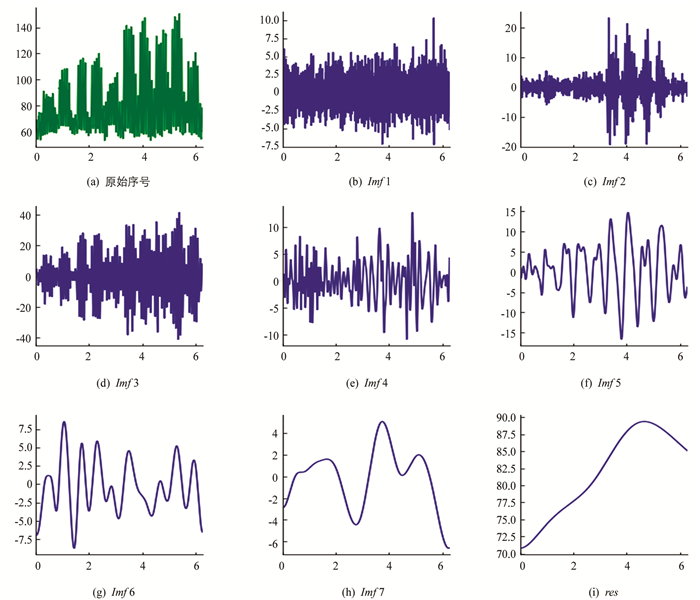
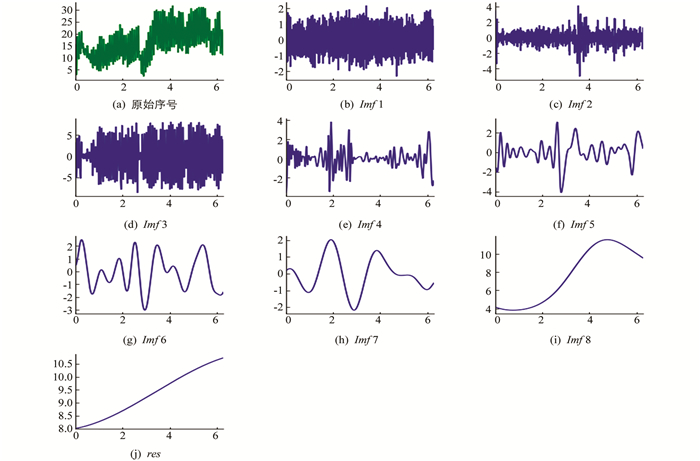
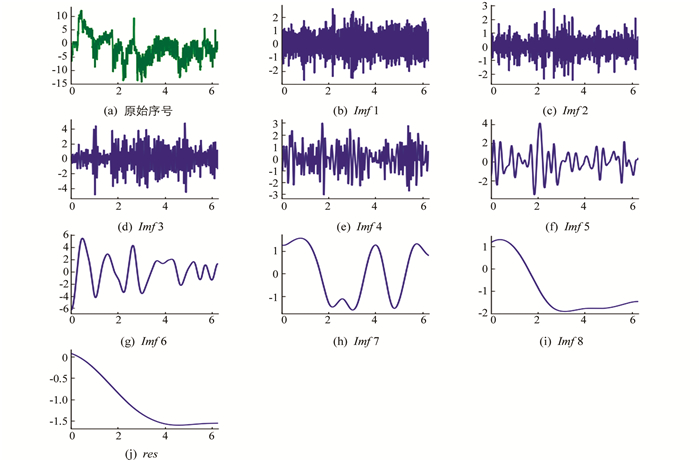
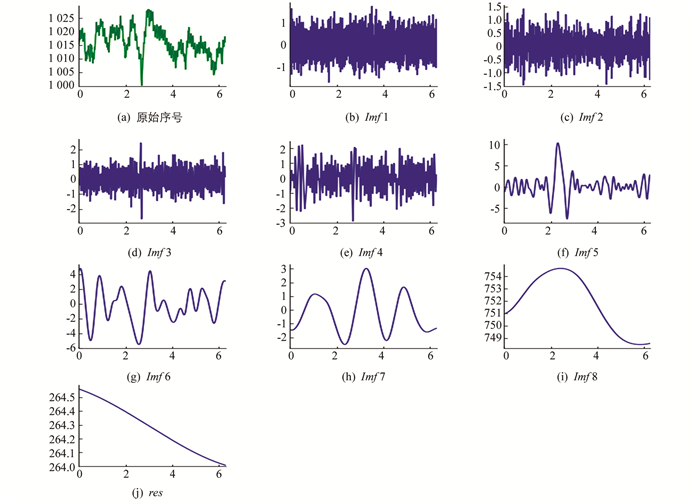
使用EEMD分解经数据处理后的用电负荷数据序列和影响因素数据序列(空气温度、露点温度和海平面气压).每次分解添加50次白噪声,各数据序列的分解结果如图 2-图 5所示.
-
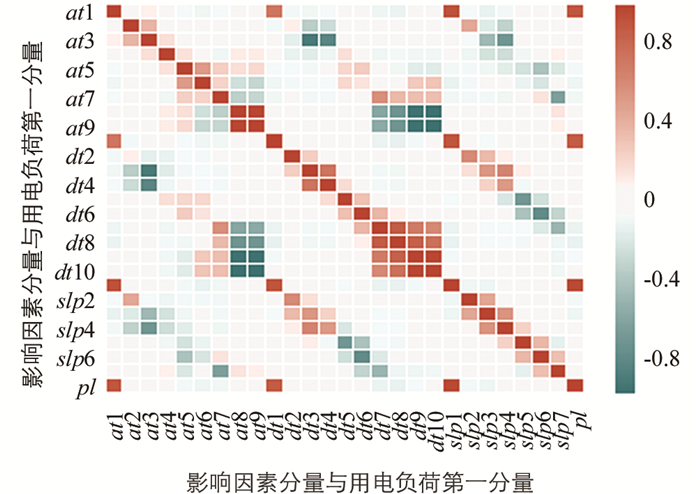
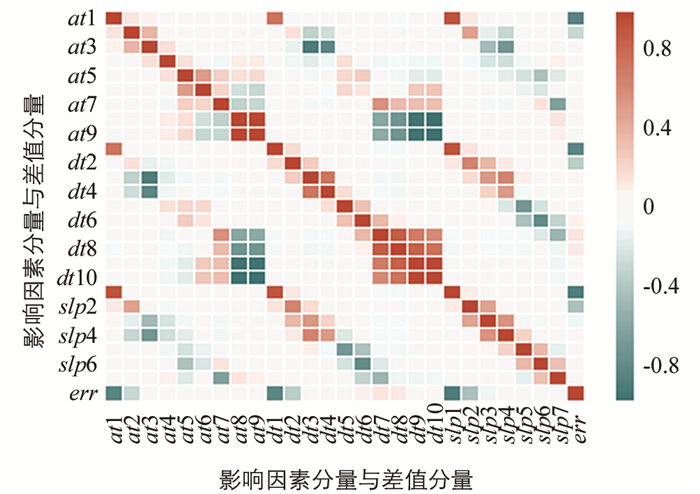
通过分析用电负荷数据经EEMD分解后的分量,本文选择使用构建的LSSVR模型预测用电负荷数的第一个Imf分量和差值序列,其中差值序列通过用电负荷数据与EEMD分解后的各分量之和的差值来表示.首先通过皮尔逊相关性分析要预测的分量以及各影响因素数据分解后的分量序列. 图 6、图 7是其分析结果图.
其中p1表示用电负荷数据的第一分量序列,err表示差值序列,at1表示空气温度数据的第一分量,dt1表示露点温度数据的第一分量,slp1表示海平面气压的第一分量,依此类推.
通过皮尔逊相关分析,本文选择的LSSVR模型的预测序列和输入分量如表 1所示.
-
通过ARIMA模型对用电负荷数据的低频分量进行预测,首先通过单位根检验(ADF)验证模型的平稳性,对非平稳序列通过差分处理进行平稳化.将最终满足平稳序列的数据通过自相关函数(ACF)和偏自相关函数(PACF)进行定阶,最终选择的ARIMA模型参数p,d,q如表 2所示.
最后将构建的LSSVR模型和ARIMA模型预测的各分量及差值序列进行叠加求和,得到最后的预测结果.
1.1. EEMD-LSSVR-ARIMA模型
1.2. EEMD分解数据序列
1.3. 基于皮尔逊相关性进行特征选择的LSSVR建模流程
1.4. ARIMA建模流程
-
为验证EEMD-LSSVR-ARIMA混合模型的有效性,本文对模型进行了实验分析,实验数据为某建筑2016年的实际用电负荷数据共计8 784条,本文使用其中80%的数据作为训练集,20%的数据作为测试集.经分析,用电负荷数据具有以下几个特征:
1) 连续性:用电负荷数据呈现出连续变化趋势,即每2个采样点之间是连续变化的;
2) 周期性:用电负荷数据呈现出周期性变化,每隔一定时间会达到用电峰值,随后开始下降;
3) 波动性:由于受到各种因素的影响,数据在周期变化的基础上呈现出小幅波动性.
本次实验所用软件为Anaconda3,编程语言为python.
-
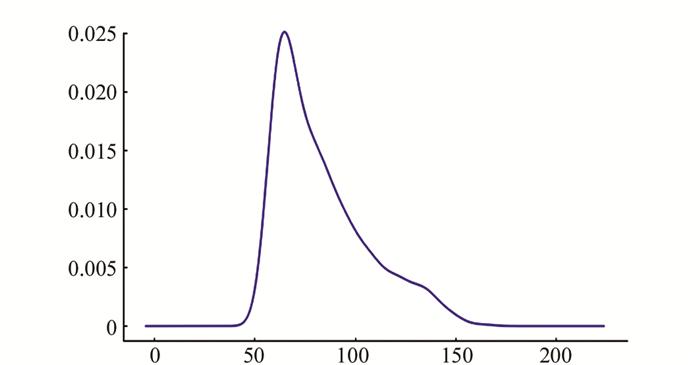
由于在数据采集过程中,受到人为因素或者外界因素干扰,导致部分数据采集不准确,会影响模型的训练效果.因此需要对数据序列中的异常数据进行处理,首先分析用电负荷数据的分布区间,结果如图 8所示.
从图 8可知,数据近似于正态分布,因此本文选择使用3σ准则判断数据中的异常值.对于检测出的异常数据本文选择使用异常值的前5个采样点和后5个采样点的均值来替换.
-
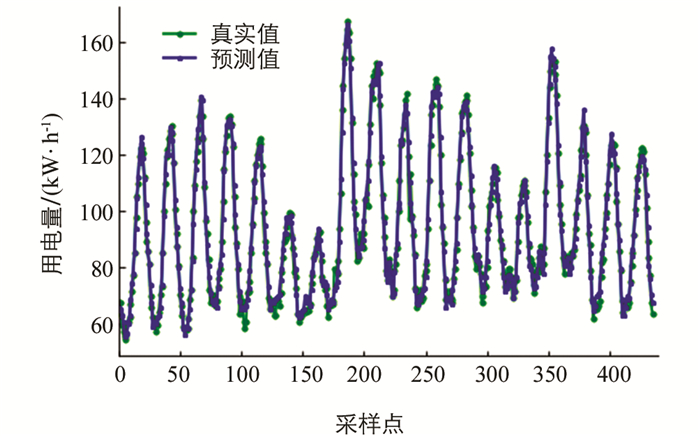
通过EEMD-LSSVR-ARIMA模型对经数据处理后的用电负荷数据进行预测,部分预测结果如图 9所示,其横坐标表示预测的采样点,纵坐标表示预测值.
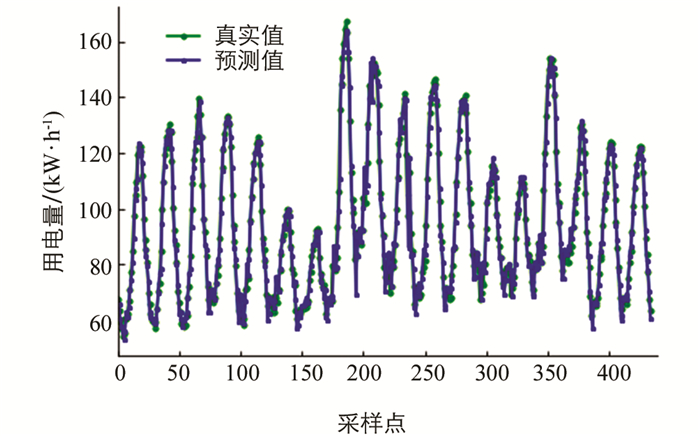
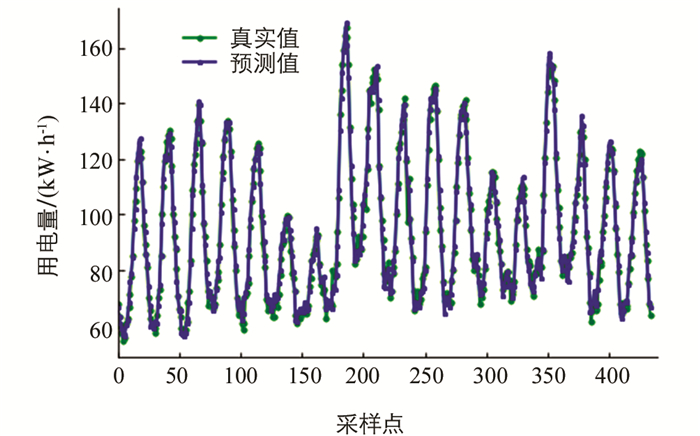
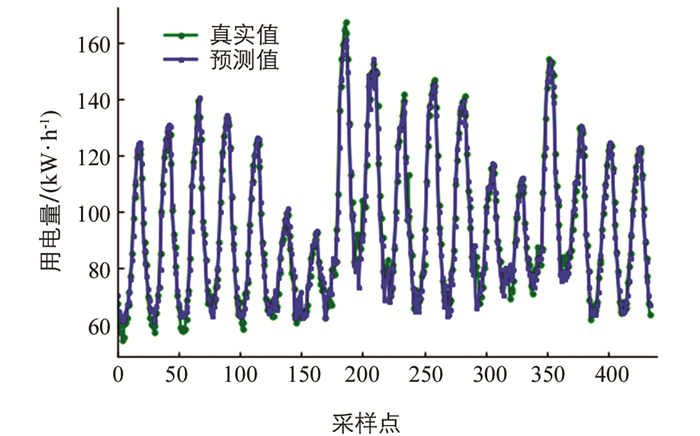
为有效分析模型,本文分别通过经典的ARIMA模型和不考虑影响因素分量的EEMD-ARIMA模型,以及基于残差的ARIMA-LSTM模型作为对比实验对同样的数据集进行了预测,部分预测结果如图 10、图 11和图 12所示.
表 3为4种模型的部分预测结果与真实值的比较.本文通过分析模型预测误差的平均绝对误差和均方根误差,以及验证模型预测数据与真实数据拟合程度的R2来分析比较4种模型,分析结果如表 4所示.
从上述对比实验可以发现,单一的ARIMA模型在所有预测模型中表现最差,基于时间序列多尺度分解但未考虑影响因素的EEMD-ARIMA模型表现优于单一的ARIMA模型,而基于残差的ARIMA-LSTM模型表现与EEMD-ARIMA模型相近,拟合度略高于EEMD-ARIMA模型,而基于时间序列多尺度分解并且考虑影响因素的EEMD-LSSVR-ARIMA模型在所有模型中表现最佳,与真实数据的拟合程度达到了98%以上,误差在4种模型中最低.
2.1. 数据来源及特点
2.2. 数据处理方法
2.3. 结果分析
-
我国作为一个能源消耗大国,对于能耗数据尤其是电力消耗数据的研究起步相对较晚,用电问题一直都是困扰我国经济发展的关键问题.本文首先整理和分析了近年来对于用电负荷预测的研究现状,针对目前的研究情况提出了自己的见解.并针对某建筑用电负荷数据特征,选择空气温度等气象数据作为影响因素,拟合建筑用电规律,提出了一种新型的基于时间序列多尺度分解的EEMD-LSSVR-ARIMA混合预测模型,并通过实验验证了模型的有效性,实现了对建筑用电负荷数据的精准预测.






 DownLoad:
DownLoad: