-
随着空间数据的激剧增多,空间数据挖掘在测绘、导航、环境保护、公共交通、位置服务和城市计算等领域得到广泛应用.空间co-location模式挖掘是空间数据挖掘的重要分支,旨在挖掘其实例在空间中频繁关联的空间特征的子集,例如小丑鱼通常居住在海葵的触手之间,商场附近总是有KTV[1].传统co-location模式采用团实例模型,该模型要求模式实例中的特征实例两两邻近形成团,从而忽略了空间特征间重要的非团的空间关系.针对这个问题,文献[2-3]提出了更具普适性的星型实例模型及亚频繁co-location模式,该模型放松了团约束,可以发现空间特征间更丰富的空间关系.
然而,上述星型实例模型及亚频繁co-location模式没有考虑空间数据的时间特性,而时间却是空间数据的关键要素.在现实世界中,空间实例的生存或位置会随着时间的变化而变化,例如,医院、学校等特征的实例有生命期,人、车等特征的实例会移动.在这样的时空数据上挖掘co-location模式,不同的时间将会得到不同的模式,即co-location模式也会随着时间的变化而变化,例如:{人,车,餐厅}是早上6点到8点的一个co-location模式;而{人,办公楼}是上午9点到12点的一个co-location模式.此外,分析不同时间的co-location模式及其随时间的变化规律,将有助于我们进一步了解空间特征间的时空关系,为co-location模式在环境保护、公共交通、位置服务和城市计算等领域的深入应用提供决策支持.
基于上述分析,本文考虑空间实例的位置随着时间变化而变化,研究基于星型实例模型的时空亚频繁模式挖掘.本研究主要面临2个方面的挑战:①基于星型实例模型及亚频繁模式,如何有效地融入时间信息并合理地定义时空亚频繁模式? ②面对计算更为复杂的时空数据,如何高效地挖掘时空亚频繁模式?
具体地,本研究主要工作包括:
(1) 分析融入时间信息的方式,提出时空亚频繁co-location模式及其度量指标:时间亚频繁度.
(2) 证明时空亚频繁模式的反单调性(向下闭合性),提出有效的时空亚频繁模式挖掘算法.
(3) 在合成数据集基础上进行大量实验,验证了所提算法的有效性及时空亚频繁模式的实用性.
HTML
-
根据所采用的实例模型,空间co-location模式主要可以分为2类:基于团实例模型的co-location模式和基于星型实例模型的co-location模式.
-
基于团实例模型的co-location模式由文献[4]提出,该模型要求模式实例中的特征实例两两邻近形成团,并采用参与度(最小参与率)度量模式的频繁程度.为了提高模式挖掘效率,文献[4]证明了参与度的反单调性(向下闭合性),并提出了基于完全连接的join-based算法.针对生成候选模式实例时大量连接操作导致算法效率低的问题,文献[5]通过划分特征实例,提出了基于部分连接的partial join算法;文献[6]采用星型邻居实例及模式实例查找方法,提出了无连接的join-less算法.而文献[7-9]采用前缀树降低模式实例生成代价,分别提出了基于CPI-tree结构的无连接算法[7],基于iCPI-tree结构的模式挖掘算法[8],以及基于有序团的极大模式挖掘算法[9].
在团实例模型下,研究者从效用、不确定性、模糊性等方面对co-location模式进行了广泛研究[10-12].研究者也引入时间维度,进行了时空数据上的co-location模式研究.文献[13]计算各个时间片上的模式参与度,然后通过标准化欧式距离计算最终的模式参与度;文献[14]定义了空间上邻近且时间上持久但不一定邻近的混合对象组,提出了一种混合驱动时空共现模式挖掘算法MDCOPs;文献[15]提出了top-k MDCOPs算法;文献[16]进一步考虑对象的生存周期,提出了PACOPs算法;文献[17]采用加权滑动窗口模型,进一步考虑各时间片间的关联关系,在多个时间片上挖掘模式;文献[18]基于动态增量滑动窗口从时空事件流中挖掘时空共现模式.文献[19]考虑交通数据的时空特性,提出采用参与度和传播影响力度量模式有趣性,挖掘频繁同现且具有强传播影响力的拥堵模式.
-
基于星型实例模型的co-location模式由文献[2-3]提出,该模型放宽了团约束条件,仅需模式实例中的特征实例与中心特征实例邻近,从而可以发现更丰富的空间关系.文献[2-3]针对传统团实例模型及co-location模式的不足,提出星型实例模型及亚频繁co-location模式,并证明了亚频繁模式的反单调性,提出了2种高效的极大亚频繁模式挖掘算法,即基于前缀树的算法PTBA和基于分区的算法PBA;文献[20]考虑空间特征间的主导关系,定义了亚频繁模式中的主导特征及主导特征模式,提出了有效的挖掘算法.
与上述研究不同,本文考虑空间实例的时间特性,研究时空亚频繁co-location模式挖掘.
1.1. 基于团实例模型的co-location模式
1.2. 基于星型实例模型的co-location模式
-
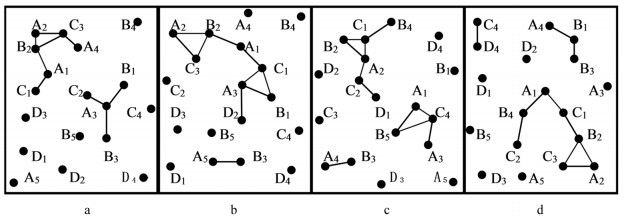
空间特征表示空间中不同种类的事物(如学校),空间特征的集合记为F={f1,f2,…,fn}.空间实例是空间特征出现在具体位置上的实例(如云南大学),空间实例的集合记为S=S1∪S2∪…∪Sn,其中Si(1≤i≤n)表示特征fi的实例集.如果两个空间实例Oi,Oj∈S的距离dis(Oi,Oj)小于给定距离阈值d,即distance(Oi,Oj)≤d,称这2个实例满足空间邻近关系R,记为R(Oi,Oj).空间co-location模式P是空间特征集合F的一个子集,即P⊆F.空间co-location模式P中空间特征的个数称为模式P的阶.在图 1(a)中,A是空间特征,A1是特征A的一个空间实例,实例A1和C1之间的连线表示它们满足空间邻近关系,即R(A1,C1). {A,B}是一个2阶模式.空间co-location模式挖掘的目标是挖掘满足一定条件(如参与度大于最小参与度阈值)的频繁模式.本研究考虑时空数据中空间实例的位置时变性,即给定时间片集合T={t0,t1,…tm-1},每个时间片上的空间特征集和空间实例集相同,但是空间实例在不同时间片上的位置可能不同. 图 1所示的时空数据集显示了4个特征的18个实例在4个时间片上的位置变化.
-
本节给出基于星型实例模型的亚频繁co-location模式相关定义.
定义1 星型邻居实例(SNsI).给定空间实例Oi,距离阈值d,Oi的星型邻居实例集合SNsI(Oi)定义为:SNsI(Oi)={Oj|distance(Oi,Oj)≤d}.
在图 1(a)所示,
$ {\rm{SNsI}}\left( {{A_1}} \right) = \left\{ {{A_1}, {B_2}, {C_1}} \right\}, {\rm{SNsI}}\left( {{A_3}} \right) = \left\{ {{A_3}, {B_1}, {B_3}, {C_2}} \right\} $ .定义2 星型参与实例(SPIns).特征f在co-location模式P中的星型参与实例表示为SPIns(f,P),是由f的实例组成的集合,其星型邻居实例包含P中的所有特征.
在图 1(a)中,
$ {\rm{SPIns}}\left( {A, \left( {A\;B\;C} \right)} \right) = \left\{ {{A_1}, {A_2}, {A_3}} \right\}, {\rm{SPIns}}\left( {B, \left( {A\;B\;C} \right)} \right) = \left\{ {{B_2}} \right\} $ .定义3 星型参与率(SPR).特征f在co-location模式P中的星型参与率SPR(f,P)是特征f的星型参与实例数与f的实例数的比率,即
$ {\rm{SPR}}\left( {f, P} \right) = |{\rm{SPIns}}\left( {f, P} \right)|/|{S_f}| $ ,其中,Sf是f的实例集合.在图 1(a)中,SPR(A,(A B C))=3/5.
定义4 星型参与度(SPI).星型参与度SPI(P)是co-location模式P中所有特征的最小星型参与率,即
$ {\rm{SPI}}\left( P \right) = \mathop {\min }\limits_{f \in P} \left\{ {{\rm{SPR}}\left( {f, P} \right)} \right\} $ .在图 1(a)中,SPI(A B C)=min(3/5,1/5,1/4)=1/5.
定义5 亚频繁co-location模式(SCP).如果co-location模式P的星型参与度不低于给定的空间亚频繁阈值θ,即SPI(P)≥θ,则模式P称为亚频繁co-location模式.
在图 1(a)中,假设θ=1/5,那么模式(A B C)为亚频繁co-location模式.
-
本文关注空间实例的位置随时间变化而变化,研究基于星型实例模型的时空亚频繁co-location模式挖掘,下面给出相关定义.
定义6 时间亚频繁度(TSF).给定时间片集合T={t0,…,tm-1}上的时空数据集,亚频繁co-location模式P出现的时间片数占总时间片数的比例称为模式P的时间亚频繁度TSF(P),
其中,SPIt(P)表示时间片t上,模式P的星型参与度.
定义7 时空亚频繁co-location模式(STSCP).如果亚频繁co-location模式P的时间亚频繁度不低于给定的时间亚频繁阈值δ,即TSF(P) ≥δ,则模式P称为时空亚频繁co-location模式.
问题定义:给定时间片集合T={t0,…,tm-1}上的时空数据集以及距离阈值d、空间亚频繁阈值θ、时间亚频繁阈值δ,时空亚频繁co-location模式挖掘就是找出时空数据集中所有满足阈值的模式.
2.1. 亚频繁co-location模式[2-3]
2.2. 时空亚频繁co-location模式
-
首先,提出一种朴素算法,然后,证明时间亚频繁度的反单调性(向下闭合性),并基于反单调性,提出新的高效的时空亚频繁模式挖掘算法(STSCP,SpatioTemporal Sub-prevalent Co-location Patterns mining algorithm).
-
朴素算法的基本思想是:首先,对每个时间片,使用空间亚频繁模式挖掘算法,挖掘所有空间亚频繁模式;然后,在所有时间片上,计算这些模式的时间亚频繁度,以挖掘时空亚频繁模式.朴素算法会尽早删除空间上不满足空间亚频繁阈值的模式,但在生成所有时间片的空间亚频繁模式之前,它不会尽早删除时间上不满足时间亚频繁阈值的模式,这导致了不必要的计算成本.
-
根据文献[2-3],星型参与度具有反单调性(向下闭合性),即给定时间片t及其上的两个模式Pi和Pj,如果Pi⊆Pj,则SPIt(Pi)≥SPIt(Pj).因此,如果Pi不是空间亚频繁模式(即SPIt(Pi)<θ),则Pj也不是空间亚频繁模式(即SPIt(Pj)<θ).
本研究所提的时间亚频繁度也具有反单调性(向下闭合性),下面给予证明.
引理1 (时间亚频繁度TSF的反单调性)给定时间片集T及其上的2个模式Pi和Pj,如果Pi⊆Pj,则TSF(Pi)≥TSF(Pj).
证 对于任一时间片t∈T,因为SPIt(Pi)≥SPIt(Pj),所以如果SPIt(Pj)≥θ,则SPIt(Pi)≥θ.因此有{t|SPIt(Pj)≥θ,t∈T}⊆{t|SPIt(Pi)≥θ,t∈T}.所以,TSF(Pi)≥TSF(Pj).
根据引理1,有如下引理2.
引理2 给定时间片集T及其上的2个模式Pi和Pj,如果Pi⊆Pj且Pi不是时空亚频繁模式(即TSF(Pi)<δ),则Pj也不是时空亚频繁模式(TSF(Pj)<δ).
利用引理2,本研究提出新的高效的时空亚频繁模式挖掘算法STSCP.算法STSCP的基本思想是采用“候选生成—亚频繁测试”方式,从1阶开始,逐阶挖掘时空亚频繁模式,并在候选生成中,利用引理2删除不可能满足条件的候选模式.具体地,仅用k阶亚频繁模式,连接生成k+1候选模式;如果k+1阶候选模式的某个k阶子模式不是亚频繁模式,则删除该k+1阶候选模式;测试剩余候选模式是否是亚频繁模式.算法STSCP描述如表 1所示.
在算法中,步骤1-2用于为每个时间片生成星型邻居实例集;步骤5-12给出一个迭代过程,直至生成的高阶时空亚频繁模式集为空.该迭代过程的功能解释如下.
生成候选时空亚频繁模式(步骤6):仅用k阶时空亚频繁模式,连接生成k+1阶候选时空模式,如果k+1阶候选时空模式的某个k阶子模式不是时空亚频繁模式,则删除该k+1阶候选时空模式.
生成候选空间亚频繁模式(步骤8):对时间片t,初始时,k+1阶候选时空模式为其上的k+1阶候选空间模式.如果k+1阶候选空间模式的某个k阶子模式不是其上的空间亚频繁模式,则从时间片t上删除该k+1阶候选空间模式.
生成星型参与实例(步骤9):对时间片t,生成其上候选空间模式的星型参与实例.
生成空间亚频繁模式(步骤10):对时间片t,计算其上k+1阶候选空间模式的星型参与度,生成k+1阶空间亚频繁模式.
生成时空亚频繁模式(步骤11):采用时间亚频繁表记录时间片0~t上的k+1阶空间亚频繁模式及其当前的时间亚频繁度.如果k+1阶空间亚频繁模式的时间亚频繁度小于δ-(1-(t+1)/|T|),则删除该k+1阶空间亚频繁模式(即k+1阶候选时空模式),后继时间片不需再处理,从而尽早删除不满足时间亚频繁阈值的模式,减少不必要的计算,提高挖掘效率.
3.1. 朴素算法
3.2. STSCP算法
-
数据集:根据文献[2-3]提供的方法,生成8个不同规模的合成数据集,这些数据集的生成参数如表 2第1-4行所示.
对比算法:为了评估本研究所提的朴素算法和STSCP算法,选用空间极大亚频繁模式挖掘算法PTBA[2-3],以及将PTBA与时间亚频繁度结合形成的算法PTBA*作为基准算法.
-
首先,从实例数、特征数、时间片数、空间亚频繁阈值、时间亚频繁阈值、距离阈值6个方面,分析它们对算法效率的影响.
-
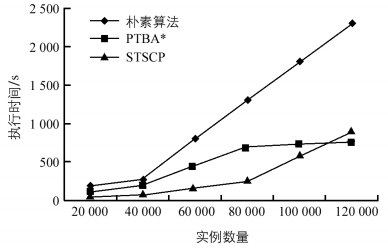
采用表 2实验一所示数据集及参数,评估实例数对算法效率的影响,结果如图 2所示.朴素算法的执行时间始终高于STSCP和PTBA*.当实例数量较小时,数据集比较稀疏,STSCP比PTBA*快.随着实例数越来越多,数据集越来越密集,相比PTBA*,STSCP执行时间增加加快.这是因为STSCP是从1阶(低阶)开始,自下而上生成所有时空亚频繁模式,而PTBA*算法是从n阶(高阶)开始,自上而下生成极大空间亚频繁模式,在稀疏数据集上,极大模式倾向于低阶模式,所以STSCP比PTBA*更快.而当数据密集时,极大模式倾向于高阶模式,所以PTBA*比STSCP更快.
-
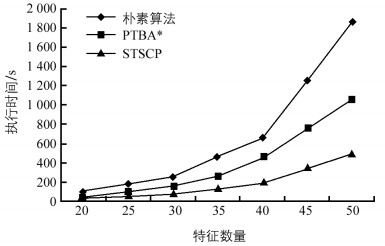
采用表 2实验二所示数据集及参数,评估特征数对算法效率的影响,结果如图 3所示.随着特征数的增加,3个算法的执行时间增加,但是STSCP均比PTBA*和朴素算法快.在实例数不变,特征数增加的情况下,每个特征的平均实例数减少,使得每个时间片上的数据稀疏,从而STSCP比PTBA*快.
-
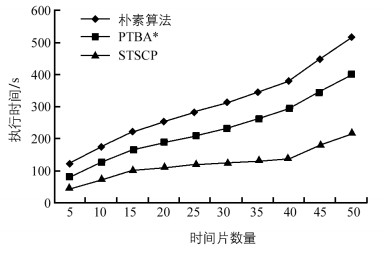
采用表 2实验三所示数据集及参数,评估时间片数对算法效率的影响,结果如图 4所示. 3个算法的执行时间随着时间片数的增加而增加,STSCP比朴素算法快是因为STSCP会尽早删除非时空亚频繁模式.而STSCP比PTBA*快是因为随着时间片数的增加,每个时间片上的数据变得稀疏.
-
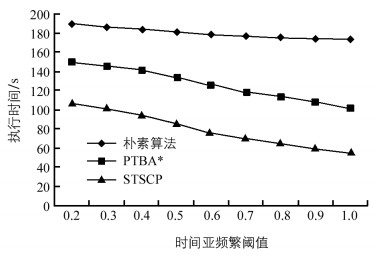
采用表 2实验四所示数据集及参数,评估时间亚频繁阈值对算法效率的影响,结果如图 5所示.从图中可以看出,3个算法的执行时间随着时间亚频繁阈值的增加而减少,且STSCP比PTBA*和朴素算法具有更高的效率.此外,由于朴素算法不能尽早删除不满足时间亚频繁阈值的模式,它的执行时间减少较缓慢.
-
采用表 2实验五所示数据集及参数,评估空间亚频繁阈值对算法效率的影响,结果如图 6所示.随着空间亚频繁阈值的增加,STSCP、PTBA*、朴素算法的执行时间减少.空间亚频繁阈值较小时,朴素算法的执行时间远高于STSCP和PTBA*,这是因为朴素算法往往会生成大量非时空亚频繁模式.对于STSCP和PTBA*,当空间亚频繁阈值较小时,STSCP的执行时间比PTBA*减少速度更快,而当空间亚频繁阈值达到0.5以后,PTBA*的执行时间比STSCP减少速度更快.
-
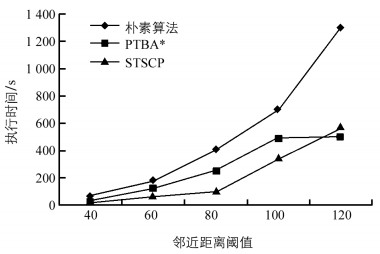
采用表 2实验六所示数据集及参数,评估邻近距离阈值对算法效率的影响,结果如图 7所示.随着邻近距离阈值增大,STSCP、PTBA*、朴素算法的执行时间呈上升趋势.当距离阈值小于100时,虽然STSCP比朴素算法和PTBA*更快,但3种算法的执行时间都在快速增加,这是因为邻近距离阈值增加可能导致2阶模式空间亚频繁模式增加.当距离阈值大于100后,PTBA*比STSCP快,这是因为邻近区域足够大,PTBA*可以比STSCP更早停止.
-
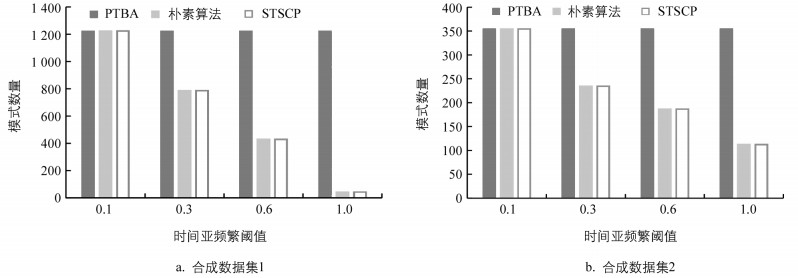
为了分析本研究所提时空亚频繁模式与文献[2-3]所提空间亚频繁模式的差异,采用表 2实验七和实验八所示数据集及参数,评估时间亚频繁阈值对本文所提算法STSCP与文献[2-3]所提算法PTBA挖掘结果的影响,结果如图 8所示.随着时间亚频繁阈值的增加,PTBA挖掘出的模式数量一直保持不变,而STSCP挖掘出的模式数量一直在减少,这是因为PTBA是在空间上挖掘亚频繁模式,挖掘结果不受时间亚频繁阈值的影响,而对于STSCP随着时间亚频繁阈值的提高,要求模式出现在更多的时间片上,从而符合要求的模式越来越少.从图 8可以看到,当时间亚频繁阈值为0.1时,模式只需要在一个时间片上出现,这相当于没有时间约束,此时STSCP挖掘的模式数量与PTBA相同,而当时间亚频繁阈值为1时,要求模式在所有时间片上出现,符合要求的模式数量最少,所以STSCP挖掘的模式数量远低于PTBA.
在现实中,用户需求的模式可能是多次出现的模式,也可能是瞬时出现的模式.本研究所提算法STSCP可以根据用户设定的时间亚频繁阈值,挖掘不同出现频度的时空亚频繁模式,而PTBA只能挖掘一种出现频度的时空亚频繁模式,因此STSCP可以挖掘更符合用户需求、更具有丰富语义也更具有实用价值的模式.
4.1. 实验设置
4.2. 算法效率分析
4.2.1. 实例数量的影响
4.2.2. 特征数量的影响
4.2.3. 时间片数量的影响
4.2.4. 时间亚频繁阈值的影响
4.2.5. 空间亚频繁阈值的影响
4.2.6. 邻近距离阈值的影响
4.3. 挖掘结果分析
-
时间是空间数据的重要维度,在现实世界中,空间实例的生存或位置会随着时间的变化而变化,而现有星型实例模型及亚频繁co-location模式没有考虑空间数据的时间特性.因此,本研究基于星型实例模型的时空亚频繁co-location模式挖掘.首先分析了融入时间的方式,定义了时空亚频繁模式的指标,提出了时空亚频繁co-location模式.然后,基于星型参与度的反单调性证明了时间亚频繁度满足向下闭合性,提出了有效的时空亚频繁模式挖掘算法.最后,在合成数据集基础上进行大量实验,验证了所提算法能够挖掘到更丰富、更有价值的时空亚频繁co-location模式.







 DownLoad:
DownLoad: