Search Advanced

Message Board

Dear readers, authors and reviewers,you can add a message on this page. We will reply to you as soon as possible!

2021 Volume 43 Issue 1
Article Contents
Previous Article Next Article

ZHENG Rui-lun, GAO Jun-hua, YANG Bang-chao, et al. Progress in Researches of Non-harmonic Effect of Crystal Structure Phase Transition[J]. Journal of Southwest University Natural Science Edition, 2021, 43(1): 39-51. doi: 10.13718/j.cnki.xdzk.2021.01.005
Citation: ZHENG Rui-lun, GAO Jun-hua, YANG Bang-chao, et al. Progress in Researches of Non-harmonic Effect of Crystal Structure Phase Transition[J]. Journal of Southwest University Natural Science Edition, 2021, 43(1): 39-51. doi: 10.13718/j.cnki.xdzk.2021.01.005
shu

Progress in Researches of Non-harmonic Effect of Crystal Structure Phase Transition

  • 1.

    School of Electronic Information and Electrical Engineering, Chongqing University of Arts and Sciences, Yongchuan Chongqing 402160, China

  • 2.

    School of Physical Science and Technology, Southwest University, Chongqing 400715, China

  • 3.

    College of Electronic Science and Technology, University Electronic Science Technology of China, Chengdu 610054, China

More Information
  • Corresponding author: CHENG Zheng-fu
  • Received Date: 20/03/2020
    Available Online: 20/01/2021

  • MSC: O481

  • Based on an introduction of the physical models of the non-harmonic effect of the phase transition of the solid material structure, this paper reviews the progress in the researches of the non-harmonic effect of crystal structure phase transition, such as the incommensurability of one-dimensional insulating materials with structural phase changes, two-dimensional binary alloy structural phase transition and graphene material semi-metal-antiferromagnetic-paramagnetic phase transition, and three-dimensional topological material structure phase transitions and thermoelectric material structure phase transitions, and describes the research methods we use and the important conclusions we draw. It systematically explains the role of non-harmonic effects in the phase transition of crystal materials. Finally, a prospect to the future study of non-harmonic effects in crystal structure phase transitions is given so as to provide theoretical references for the predictive design of new material structures and the regulation of material interfaces.
  • 加载中
  • [1] KITTEL C, HOLCOMB D F. Introduction to Solid State Physics[J]. American Journal of Physics, 1967, 35(6): 547-548. doi: 10.1119/1.1974177

    CrossRef Google Scholar

    [2] PYNN R. Incommensurable Structures[J]. Nature, 1979, 281(5731): 433-437. doi: 10.1038/281433a0

    CrossRef Google Scholar

    [3] JEMNON A Y. Surface Energy and Surface Tension of Solids[J]. Journal of Physical Chemistry, 1982(5): 1207-1211.

    Google Scholar

    [4] DAVYDOV S Y, TIKHONOV S K. Deformation Potential of Wide-gap Semiconductors[J]. Semiconductors, 1996, 30(6): 968-973.

    Google Scholar

    [5] 郑瑞伦, 梁一平.非简谐振动对Ag超微粒表面能的影响[J].材料研究学报, 1997, 11(1): 37-41.

    Google Scholar

    [6] 程正富, 龙晓霞, 郑瑞伦.温度对光学微腔玻色凝聚的影响[J].物理学报, 2010, 59(12): 7841-7847.

    Google Scholar

    [7] 程正富, 郑瑞伦.非简谐振动对石墨烯杨氏模量与声子频率的影响[J].物理学报, 2016, 65(10): 177-184.

    Google Scholar

    [8] CHENG Z F, ZHENG R L. Thermal Expansion and Deformation of Graphene[J]. Chin Phys Lett, 2016, 33(4): 046501-1-046501-4.

    Google Scholar

    [9] REN X X, KANG W, CHENG Z F, et al. Temperature-Dependent Debye Temperature and Specific Capacity of Graphene[J]. Chinese Physics Letters, 2016, 33(12): 105-109.

    Google Scholar

    [10] ZHENG R L. The Boyle Curve of Two-Dimensional Fluid System in the Unharmonic Vibration[J]. Commun Theor Phy, 1992, 18: 411-418. doi: 10.1088/0253-6102/18/4/411

    CrossRef Google Scholar

    [11] 郑瑞伦, 胡先权.非简谐振动对液氩的临界点与玻意耳线的影响[J].物理学报, 1994, 43(8): 1254-1261.

    Google Scholar

    [12] 郑瑞伦, 陶诒.形状和原子数对纳米晶表面能的影响[J].物理学报, 2006, 55(4): 1942-1946. doi: 10.3321/j.issn:1000-3290.2006.04.065

    CrossRef Google Scholar

    [13] 任晓霞, 申凤娟, 林歆悠, 等.石墨烯低温热膨胀和声子弛豫时间随温度变化规律研究[J].物理学报, 2017, 66(22): 224701-1-224701-9.

    Google Scholar

    [14] 杜一帅, 康维, 郑瑞伦.外延石墨烯电导率和费米速度随温度变化规律研究[J].物理学报, 2017, 66(1): 014701-1-014701-8.

    Google Scholar

    [15] 郑瑞伦, 李建, 梁一平, 等. Mo纳米晶热学特性[J].材料研究学报, 1995, 9(6): 501-504.

    Google Scholar

    [16] 郑瑞伦.激光辐照金属板材的温升和升温率[J].光子学报, 1998, 27(11): 1028-1032.

    Google Scholar

    [17] 郑瑞伦, 刘俊.强激光辐照下金属材料表面热力学效应[J].光子学报, 2002, 31(4), 480-484.

    Google Scholar

    [18] 郑瑞伦, 非简谐振动对二维系统相变及热容量的影响[J].西南师范大学学报(自然科学版), 1990, 15(1): 48-56.

    Google Scholar

    [19] 郑瑞伦, 吴兴源, 吴秀英.面心立方晶体热力学性质的非简谐效应[J].西南师范大学学报(自然科学版), 1991, 16(4): 432-439.

    Google Scholar

    [20] 郑瑞伦, 穆峰.晶体铜的表面能和表面张力[J].西南师范大学学报(自然科学版), 1993, 18(1): 26-32.

    Google Scholar

    [21] 郑瑞伦, 胡先权.面心立方晶格的非简谐效应[J].大学物理, 1994, 13(5): 15-18.

    Google Scholar

    [22] 郑瑞伦, 田维林.非简谐振动对二维流体热膨胀系数、压缩系数的影响[J].西南师范大学学报(自然科学版), 1998, 23(2): 156-161.

    Google Scholar

    [23] 郑瑞伦, 梁英贤, 龙晓霞.非简谐振动对固态方程的影响[J].西南师范大学学报(自然科学版), 2000, 25(3): 247-252. doi: 10.3969/j.issn.1000-5471.2000.03.009

    CrossRef Google Scholar

    [24] 刘俊, 郑瑞伦.低温下金属热膨胀系数的同位素效应[J].西南师范大学学报(自然科学版), 2002, 27(5): 708-712. doi: 10.3969/j.issn.1000-5471.2002.05.017

    CrossRef Google Scholar

    [25] 郑瑞伦, 田德祥, 龙晓霞.原子相互作用势对弹性模量的影响[J].西南师范大学学报(自然科学版), 2003, 28(6): 892-896. doi: 10.3969/j.issn.1000-5471.2003.06.016

    CrossRef Google Scholar

    [26] 张翠玲, 郑瑞伦.非简谐振动对Fe热容和电阻率的影响[J].西南师范大学学报(自然科学版), 2004, 29(4): 613-617. doi: 10.3969/j.issn.1000-5471.2004.04.018

    CrossRef Google Scholar

    [27] 吴强, 郑瑞伦.铁颗粒膜自旋激发谱和热力学性质研究[J].西南师范大学学报(自然科学版), 2005, 30(6): 1038-1043. doi: 10.3969/j.issn.1000-5471.2005.06.020

    CrossRef Google Scholar

    [28] 周虹君.非简谐振动对SiC的热膨胀系数和介电性能的影响[J].原子与分子物理学报, 2018, 35(5): 879-883. doi: 10.3969/j.issn.1000-0364.2018.05.027

    CrossRef Google Scholar

    [29] 郑瑞伦, 夏继宏, 杨文耀.石墨烯材料热学和电学性能研究:从非简谐效应视角[M].成都:西南交通大学出版社, 2019.

    Google Scholar

    [30] 北京大学物理系《量子统计物理学》编写组.量子统计物理学[M].北京:北京大学出版社, 1987.

    Google Scholar

    [31] 李正中.固体理论[M].北京:高等教育出版社, 2002.

    Google Scholar

    [32] 杜宜瑾, 陈立溁, 严祖同.二维相变系统Collins模型的统计理论[J].物理学报, 1983, 32(1): 96-102. doi: 10.3321/j.issn:1000-3290.1983.01.011

    CrossRef Google Scholar

    [33] KAWAMURA H. A Simple Theory of Melting and Condensation in Two-Dimensional System[J]. Progress of Theoretical Physics, 1980, 63(1): 24-41. doi: 10.1143/PTP.63.24

    CrossRef Google Scholar

    [34] DAVYDOV S Y. The Role of Electron-electron Repulsion in the Problem of Epitaxial Graphene on a Metal: Simple Estimates[J]. Physics of the Solid State, 2017, 59(8): 1674-1682. doi: 10.1134/S1063783417080078

    CrossRef Google Scholar

    [35] CHEN T, SHAO D X, LU P C, et al. Anharmonic Effect Driven Topological Phase Transition in Pb O2 Predicted by First-principles Calculations[J]. Physical Review B, 2018, 98(14): 144105-1-144105-8.

    Google Scholar

    [36] BY Yasusade Yamada, IWAO Shibuya and SADAO Hoshino. Phase Transition in NaNO2[J]. J. Phys. Soc. Jpn., 1963, 18(11): 1594-1603. doi: 10.1143/JPSJ.18.1594

    CrossRef Google Scholar

    [37] ⅡZUMI M, AXE J D, SHIRANE G, et al. Structural Phase Transformation inK2SeO4[J]. Physical Review B, 1977, 15(9): 4392-4411.

    Google Scholar

    [38] MCMILLAN W L. Theory of Discommensurations and the Commensurate-incommensurate Charge-density-wave Phase Transition[J]. Physical Review B, 1976, 14(4): 1496-1502. doi: 10.1103/PhysRevB.14.1496

    CrossRef Google Scholar

    [39] BAK P, EMERY V J. Theory of the Structural Phase Transformations in Tetrathiafulvalene-Tetracyanoquinodimethane (TTF-TCNQ)[J]. Physical Review Letters, 1976, 36(16): 978-982. doi: 10.1103/PhysRevLett.36.978

    CrossRef Google Scholar

    [40] MOMCTON D E, AXE J D, DISALVO F J. Study of Superlattice Formation in 2H-NbSe2 and 2H-TaSe2 by Neutron Scattering[J]. Phys Rev Lett, 1975, 34: 734-737. doi: 10.1103/PhysRevLett.34.734

    CrossRef Google Scholar

    [41] ZHENG R L, HU X Q. Influence of Anharmonic Vibration on the Solubility Curve of the Binary Alloy[J]. Communications in Theoretical Physics, 1996, 26(1): 39-44. doi: 10.1088/0253-6102/26/1/39

    CrossRef Google Scholar

    [42] 杜宜谨, 严祖同, 陈立荣.二元替换式的统计理论[J].物理学报, 1983, 32(7): 918-919.

    Google Scholar

    [43] 郑瑞伦, 陈怀新, 吴兴源, 等.非简谐振动对二元系统溶解限曲线的影响[J].西南师范大学学报(自然科学版), 1993, 18(3): 280-287.

    Google Scholar

    [44] ULYBYSHEV M V, BUIVIDOVICH P V, KATSNELSON M I, et al. Monte-Carlo Study of the Semimetal-insulator Phase Transition in Monolayer Graphene with a Realistic Interelectron Interaction Potential[J]. Physical Review Letters, 2013, 111(5): 056801-1-056801-7.

    Google Scholar

    [45] DAVYDOV S Y. Electron-Electron and Electron-Phonon Interactions in Graphene on a Semiconductor Substrate: Simple Estimations[J]. Semiconductors, 2018, 52(3): 335-340. doi: 10.1134/S1063782618030090

    CrossRef Google Scholar

    [46] 高君华, 郑瑞伦.金属基外延石墨烯相图非谐效应探讨[J].功能材料, 2020, 51(5): 5118-5123.

    Google Scholar

    [47] 孙鹏哲.新型二氧化铅电极的研究进展[J].广州化工, 2018, 46(20): 24-26. doi: 10.3969/j.issn.1001-9677.2018.20.012

    CrossRef Google Scholar

    [48] SCHVMANN U, GRVNDLER P. Electrochemical Degradation of Organic Substances at PbO2 Anodes: Monitoring by Continuous CO2 Measurements[J]. Water Research, 1998, 32(9): 2835-2842. doi: 10.1016/S0043-1354(98)00046-3

    CrossRef Google Scholar

    [49] RAND D A J. Lead-acid Batteries: By H. Bode, John Wiley, New York, 1977, 387 Pp[J]. Journal of Power Sources, 1979, 4(3): 252-255. doi: 10.1016/0378-7753(79)85016-8

    CrossRef Google Scholar

    [50] ZHOU Y H, LU P C, DU Y P, et al. Pressure-Induced New Topological Weyl Semimetal Phase in TaAs[J]. Physical Review Letters, 2016, 117(14): 146402. doi: 10.1103/PhysRevLett.117.146402

    CrossRef Google Scholar

    [51] BRAHLEK M, KOIRALA N, SALEHI M, et al. Disorder-driven Topological Phase Transition in Bi2Se3 Films[J]. Phys Rev B, 2016, 94(16): 165104-1-165104-5.

    Google Scholar

    [52] PAYNE D J, EGDELL R G, HAO W, et al. Why is Lead Dioxide Metallic?[J]. Chemical Physics Letters, 2005, 411(1-3): 181-185. doi: 10.1016/j.cplett.2005.06.023

    CrossRef Google Scholar

    [53] PAYNE D J, EGDELL R G, LAW D S L, et al. Experimental and Theoretical Study of the Electronic Structures of α-PbO and β-PbO2[J]. J Mater Chem, 2007, 17(3): 267-277. doi: 10.1039/B612323F

    CrossRef Google Scholar

    [54] PAYNE D J, PAOLICELLI G, OFFI F, et al. A Study of Core and Valence Levels in β-PbO2 by Hard X-ray Photoemission[J]. Journal of Electron Spectroscopy and Related Phenomena, 2009, 169(1): 26-34. doi: 10.1016/j.elspec.2008.10.002

    CrossRef Google Scholar

    [55] SCANLON D O, KEHOE A B, WATSON G W, et al. Nature of the Band Gap and Origin of the Conductivity of PbO2 Revealed by Theory and Experiment[J]. Physical Review Letters, 2011, 107(24): 246402-1-246402-5.

    Google Scholar

    [56] PAYNE D J, EGDELL R G, PAOLICELLI G, et al. Nature of Electronic States at the Fermi Level of Metallic β-PbO2 revealed by Hard X-ray Photoemission Spectroscopy[J]. Physical Review B, 2007, 75(15): 153102-1-153102-4.

    Google Scholar

    [57] GANGADHARAN R, NAMBOODIRI P N N, PRASAD K V, et al. The Lithium-Thionyl Chloride Battery-a Review[J]. Journal of Power Sources, 1979, 4(1): 1-9. doi: 10.1016/0378-7753(79)80032-4

    CrossRef Google Scholar

    [58] SHAO D X, CHEN T, GU Q Y, et al. Nonsymmorphic Symmetry Protected Node-line Semimetal in the Trigonal YH3[J]. Scientific Reports, 2018, 8: 1467-1-1467-7. doi: 10.1038/s41598-018-33025-6

    CrossRef Google Scholar

    [59] HEINEMANN M, TERPSTRA H J, HAAS C, et al. Electronic Structure of β-PbO2 and Its Relation withBaPbO3[J]. Physical Review B, 1995, 52(16): 11740-11743. doi: 10.1103/PhysRevB.52.11740

    CrossRef Google Scholar

    [60] SOUVATZIS P, ERIKSSON O, KATSNELSON M I, et al. Entropy Driven Stabilization of Energetically Unstable Crystal Structures Explained from First Principles Theory[J]. Physical Review Letters, 2008, 100(9): 095901-1-095901-4.

    Google Scholar

    [61] ONEILL C D, SOKOLOV D, HERMANN A, et al. Inelastic X-ray Investigation of the Ferroelectric Transition in SnTe[J]. Physical Review B, 2017, 95(14): 1-5.

    Google Scholar

    [62] RIBEIRO G A S, PAULATTO L, BIANCO R, et al. Strong Anharmonicity in the Phonon Spectra of PbTe and SnTe from First Principles[J]. Physical Review B, 2018, 97: 014306-1-014306-12.

    Google Scholar

  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(11)  /  Tables(3)

Export Citation
PDF
XML

Article Metrics

Article views(1564) PDF downloads(388) Cited by(0)

Access History

Other Articles By Authors

Progress in Researches of Non-harmonic Effect of Crystal Structure Phase Transition

    Corresponding author: CHENG Zheng-fu
  • Received Date: 20/03/2020
  • Available Online: 20/01/2021

Abstract: Based on an introduction of the physical models of the non-harmonic effect of the phase transition of the solid material structure, this paper reviews the progress in the researches of the non-harmonic effect of crystal structure phase transition, such as the incommensurability of one-dimensional insulating materials with structural phase changes, two-dimensional binary alloy structural phase transition and graphene material semi-metal-antiferromagnetic-paramagnetic phase transition, and three-dimensional topological material structure phase transitions and thermoelectric material structure phase transitions, and describes the research methods we use and the important conclusions we draw. It systematically explains the role of non-harmonic effects in the phase transition of crystal materials. Finally, a prospect to the future study of non-harmonic effects in crystal structure phase transitions is given so as to provide theoretical references for the predictive design of new material structures and the regulation of material interfaces.

    HTML

  • 晶体结构相变不仅是固体材料最基本的热力学性质之一，而且是获取各类新材料的重要途径.相变储能和相变材料的性质等基础理论研究为开发高效率、低成本、安全可靠的大规模储能系统提供理论支撑，是当今科技研究前沿之一，而非简谐效应在晶体结构相变中起着十分重要的作用，研究晶体结构相变中非简谐效应是国内外研究的重要领域.

    自1935年非简谐效应概念提出以来，人们对固体材料非简谐效应开展了大量的研究.研究的方法涉及经典、半经典半量子、量子力学和密度泛涵理论等理论方法和用X射线非弹性散射和中子衍射直接观察声子的组合、衰变和散射等实验方法，研究内容涉及固体的力学、热学、电学和光学等性质[1-28]，但这些研究还不够深入和系统.为了系统研究固体材料非简谐效应，本课题组在文献[29]中提出了非简谐理论和方法，但如何应用该理论和方法来研究在理论和应用上都非常重要的晶体结构相变非简谐效应，未作论述.为此，本文将在论述研究固体结构相变非简谐效应物理模型的基础上，论述NaNO2亚铁磁材料不可通约结构相变、二元合金结构相变、外延石墨烯电磁三态相变和PbO2拓扑材料结构相变及SnTe热电材料结构相变等晶体材料结构相变中非简谐效应的研究进展情况，以及本课题组近20年来的研究成果，并对该领域的研究进展予以预测，为新材料的预测设计提供理论参考.

1.   研究晶体材料结构相变非简谐效应的物理模型

  • 物体内原子的运动是非简谐振动而不是简谐振动.若将它作为简谐振动处理，这称为简谐近似；非简谐与简谐近似的差对物体性质的影响称为非简谐效应.非简谐效应的大小由原子相互作用势能φ随位移δ的级数展开形式：φ=φ(0)+(1/2)ε0δ2+ε1δ3+ε2δ4+…中的非简谐系数ε1，ε2，…来体现，以此为基础的理论称为非简谐效应理论.

    为了研究晶体材料结构相变非简谐效应，除实验方法和用密度泛函理论第一性原理等计算方法外，较为简便并能体现结构相变物理过程、揭示相变随温度的变化规律的是采用非简谐理论的研究方法，方法的关键是建立合理的物理模型.对研究晶体材料的结构相变，其物理模型可分为：一维、二维、三维模型，常见的几种模型见表 1.

2.   一维不可通约结构相变与非简谐效应

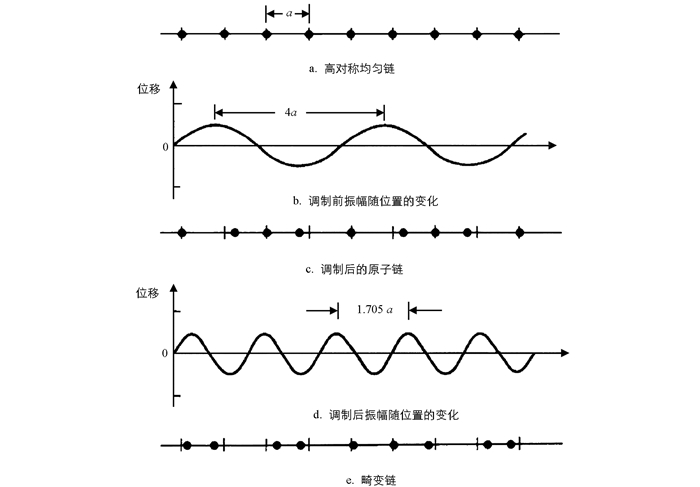
  • NaNO2这种亚铁磁性材料，除具有通常绝缘体材料的用途外，还具有许多特殊功能.文献[36]发现，随着温度等外界扰动的发生，NaNO2在晶体结构上会发生不可通约结构相变.为了从微观上研究这种结构转变，文献[2]将一个连续的位移型结构转变用图 1所示的一维原子链位移型结构相变模型来描述.

    假设高对称均匀链上均匀分布的原子，晶格常数为a(图 1a)；受到纵向(左-右)位移，其振幅在空间中呈正弦变化(图 1b).由此调制产生的原子位置将如图 1c所示，调制后振幅变化如图 1d，当调制幅值消失时，成为图 1e所示的畸变链，它与高对称均匀链之间发生了跃变，这种跃变称为不可通约材料结构相变.

    不可通约材料结构相变是非简谐效应的结果.原因在于绝缘体材料中会出现不同范围和相似大小的相互竞争的短程原子间相互作用力，由此产生一个不可通约调制的相位，进而导致绝缘体材料中出现相变.要粗略地了解其发生的原因，可用图 1a的单原子链说明.

    设只有第一和第二相邻原子之间的弹性力才贡献能量，则系统原子相互作用能量可写为

    其中：un是第n个原子对晶格平衡位置的纵向位移，A1和A2分别是第一和第二近邻谐波力常数(简谐系数).将un用傅里叶级数展开，有

    代入(1)式，得到系统的能量为

    若(2)式中Aq有一个非零波矢量q0的最小值，则正弦调制结构将是稳定的，必要条件是：

    此时的波矢量q0将满足：

    就要求：A1＜4|A2|，A2＜0，这就是系统稳定的条件.

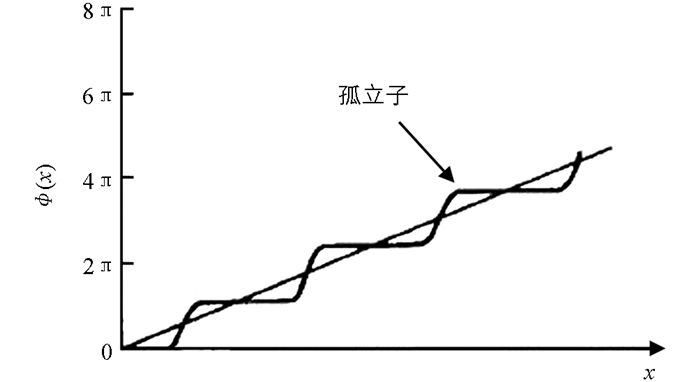
    文献[37]表明：绝缘体K2SeO4材料在130 K的温度时会转变成不可通约性的相，证实了上述计算的合理性，而且论证了原子间短程力之间的竞争是观测到相变的原因.但上述对绝缘体材料不可通约的结构相变的解释存在不足.首先，方程(1)所示的总能量以位移u为变量，其截断展开式中应该有更高阶的项(非简谐项)，以限制不可通约畸变的幅度，而方程(1)是无界的；其次，方程(1)是零温度近似，在有限温度下不适用.为了正确解释绝缘体材料不可通约的结构相变，应考虑总能量以位移u为变量的截断展开式中的更高阶的项(非简谐项).如图 1，在可调制的结构中(图 1c)，相对于均匀晶格(图 1a)，非简谐项确定了畸变的最佳相位(图 1b).为了确定非简谐项引起畸变的最佳相位，文献[38]将(2)式中离散原子位置(na)用连续坐标x代替，写为

    其中：qc是一个可通约的波矢量，它接近于由方程(3)导出的正弦畸变的波矢量；φ(x)是一个相位，它随位置x的变化，要使得方程(3)被非简谐(非截断)观点替换时能量最小.这个极小化过程产生的方程称为(静态)Sine-Gordon方程[39]，这个非线性微分方程的解与图 2中的阶梯曲线类似，而图 2中的直线表示一个波矢量的简单正弦调制变化，即简谐情况.

    文献[39]应用“最佳相位”的论点使非简谐能量最小化的过程和结果，为Moncton等对2H-TaSe2进行的中子散射实验[40]所证实.

3.   二维结构相变与非简谐效应

  • 二维结构相变在1985年前研究较多的是二元合金材料结构相变，而近些年来则研究较多的是二维铁磁-顺磁相变和导体-绝缘体-半金属的相变，但这些研究论述非简谐效应很少.这里将在简介二元合金材料结构相变非简谐效应基础上，较深入论述二维外延石墨烯的电磁三态相变的非简谐效应.

    • 3.1.   二元合金材料结构相变与非简谐效应

  • 合金材料的结构相变是普遍存在、应用最广的晶体材料结构相变之一，它涉及各类特殊钢材、特殊铝合金等在工业、日常生活、科学技术和航天航空等领域中的应用.二元合金材料结构相变的性质、规律是国内外研究的重要方面，但主要是实验或宏观理论研究，而从微观理论角度研究则较少，特别是对它的非简谐效应研究很少.

    为了研究二元合金的结构相变和它的溶解限曲线，1983年文献[32]提出了二元合金的二维Bernal晶格模型，用二维二元统计理论，得到二元合金溶解限曲线，但未考虑到原子的非简谐振动，结果与实际差异大.为了正确解释实验结果，考虑到非简谐效应，文献[41-43]研究了二元合金溶解限曲线变化规律和原子非简谐振动对它的影响.

    文献[43]采用二维Bernal晶格模型来研究二元合金[25]，认为a和b两种原子无规地分布于Bernal晶格上，其中一种配置见图 3.

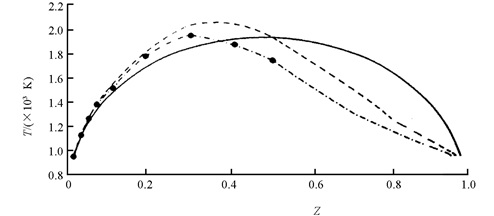
    设系统N个原子中，a和b原子分别有Na和Nb个，原子的质量为μa和μb. a和b组元中第r组元的原子数分别为Nar和Nbr(r=4，5α，5β，6).令nar=Nar/N. nbr=Nbr/N，则$\sum\limits_r {\left( {{n_{{\rm{a}}r}} + {n_{{\rm{b}}r}}} \right) = 1} $.参数x，y，m和z中，定义：x=na5α+na5β+nb5α+nb5β，m=(na5α+nb5α)/x，$z = \sum\limits_r {{n_{{\rm{a}}r}}} $.按此定义，x表征N个原子中，出现5α-原子和5β-原子的概率. x=0对应固相；x≠0，对应液相. y表征出现4-原子的概率，m表征5α-原子与5β-原子两种结构的比例关系，Z表a原子占原子数的比例.若a组元作溶质，b组元做溶剂，则Z可理解为二元合金的溶解度.

    原子不是静止而是在作非简谐振动.设a和b原子振动的简谐系数分别为εa0，εb0，第一非简谐系数为εa1和εb1，第二非简谐系数为εa2和εb2.文献[41, 43]应用二维系统的统计理论，求出考虑到原子分布和平动、振动随机性情况下，系统的特性函数自由能F为平动自由能F0与振动贡献的自由能ΔF之和，即F=F0+ΔF，其中平动自由能F0=NkBT，简谐近似，考虑到第一非简谐项时和同时考虑到第一、第二非简谐项时，原子振动对自由能的贡献ΔF0=NkBTΔf0，ΔF1=NkBTΔf1和ΔF2=NkBTΔf2与简谐系数εa0和εb0、第一非简谐系数εa1和εb1、第二非简谐系数εa2和εb2的关系，以及原子相互作用能和溶解度Z、温度T等的关系见文献[41, 43].由平衡时自由能极小的条件，求出溶解度Z随温度T变化的解析式[41].结果表明：在满足该表示式的溶解度Z和温度T的状态(即溶解限曲线上的一个点对应的状态)下，系统发生固相-液相的结构相变.对系统TiCu合金作具体计算，得到的溶解度Z随折合温度t=kBT/ε的变化见表 2，而溶解限曲线见图 4[43]，图 4中的实线为不考虑振动的结果；虚线为简谐近似的结果；带黑点的虚线为同时考虑到第一、第二非简谐项的结果；黑点为实验值. 图 4表明：在溶解度为Z，温度为T时会发生固相-液相的结构相变.

    由图 4看出：考虑到原子振动后，溶解限曲线不再具有对称性，而且非简谐情况的曲线的不对称性比简谐近似更突出；考虑到非简谐振动项，其理论值更接近实验值.例如：溶解度Z=0.04时，溶解温度实验值为T=1 125 K，不考虑非简谐时为T=1 139 K，误差为1.24%；考虑到非简谐为T=1 126 K，误差为0.09%.

    • 3.2.   二维外延石墨烯相图与非简谐效应

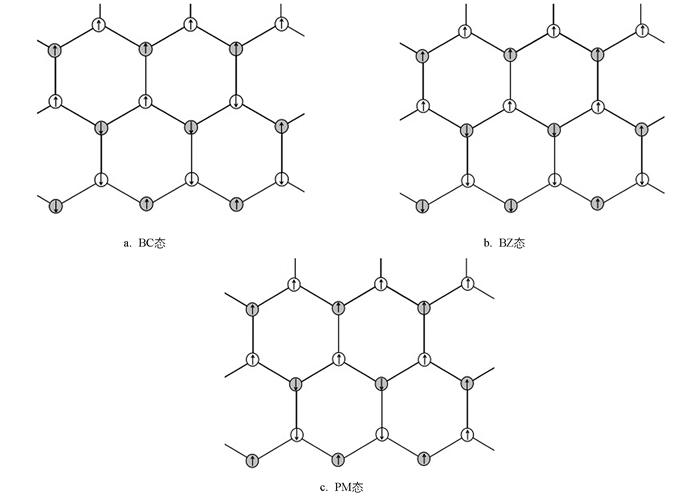
  • 除原子组成结构的状态变化引起的结构相变外，原子内电子自旋状态的变化也会引起结构相变. 2013年文献[44]对石墨烯电磁学性质的转变问题进行了研究，证明考虑到电子自旋后，石墨烯原子内部电子关联U和原子间电子关联G的变化，使系统可处于零自旋磁矩的半金属态(PM态)、自旋磁矩相反的自旋密度波状态(BC态)和自旋磁矩相同的电荷密度波状态(BZ态)这3种状态，材料分别表现为半金属性、反铁磁性和顺磁性. 2017年文献[34]进一步证明：金属基外延石墨烯同样会出现上述情况，但对相变条件以及电子关联的影响并未深入论述，而且未考虑原子的振动.这里研究非简谐效应对金属基外延石墨烯相图的影响.

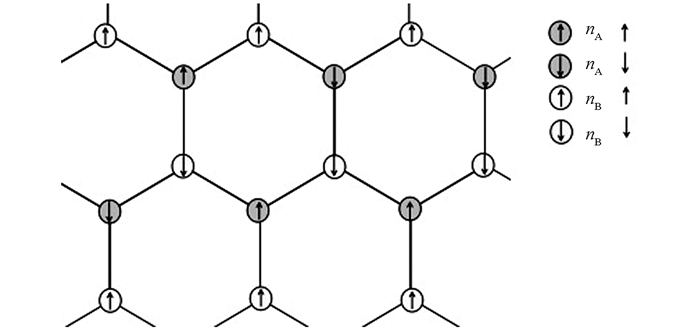
    单层外延石墨烯的俯面见图 5，它是由A和B子格组成的复式格子，各子格原子中的电子有自旋，自旋为ћ/2的状态用↑表示，自旋为-ћ/2的状态用↓表示.

    A原子中自旋为ћ/2的状态电子填充数记为nA↑，而自旋(-ћ/2)状态填充电子数为nA↓；同样，B原子中自旋为ћ/2和-ћ/2的状态填充数为nB↑和nB↓.按照电子填充情况，系统会出现3种状态：第1种，nA↑+nA↓=nB↑+nB↓，nA↑-nA↓≠nB↑-nB↓(图 6a)，此状态为BC态；第2种，nA↑+nA↓≠nB↑+nB↓，nA↑-nA↓=nB↑-nB↓，此状态为BZ态(图 6b)；第3种，nA↑+nA↓=nB↑+nB↓，nA↑-nA↓=nB↑-nB↓，此状态为PM态(图 6c).

    为了描述系统状态，引入序参量a，b，c和d：$a = \frac{1}{2}\left( {{n_{{\rm{A}} \uparrow }} + {n_{\rm{A}\downarrow}}, + {n_{{\rm{B}} \uparrow }} + {n_{{\rm{B}} \downarrow }}} \right)$，$b = \frac{1}{2}\left[ {\left( {{n_{{\rm{A}} \uparrow }} - {n_{{\rm{A}} \downarrow }}} \right) + } \right.\left. {\left( {{n_{{\rm{B}} \uparrow }} - {n_{{\rm{B}} \downarrow }}} \right)} \right]$，$c = \frac{1}{2}\left[ {\left( {{n_{{\rm{A}} \uparrow }} + {n_{{\rm{A}} \downarrow }}} \right) - \left( {{n_{{\rm{B}} \uparrow }} + {n_{{\rm{B}} \downarrow }}} \right)} \right]$，$d = \frac{1}{2}\left[ {\left( {{n_{{\rm{A}} \uparrow }} - {n_{{\rm{A}} \downarrow }}} \right) - \left( {{n_{{\rm{B}} \uparrow }} - {n_{{\rm{B}} \downarrow }}} \right)} \right]$，BC，BZ和PM的序参量分别是：BC(c=0，d≠0)、BZ(c≠0，d=0)、PM(c=d=0).

    不考虑石墨烯原子的振动时，电子系统的哈密顿H为基底电子哈密顿Hs、石墨烯电子哈密顿Hg和石墨烯原子与基底原子的电子相互作用哈密顿Hin之和，即

    它们与电子间的内部关联U和原子间的电子关联G等的关系见文献[45].在哈特利-福克近似下，考虑到电子自旋后金属基外延石墨烯系统的能量为

    考虑到原子作非简谐振动后，因非简谐振动要产生大量的声子，电子与声子之间有相互作用.这时，外延石墨烯电子系统的能量E为E0与电子声子相互作用能ΔEep之和：

    式中：ΔEep为一个电子和一个声子相互作用能W以及声子数nq的积，即ΔEep=Wnq.而nq为

    (10) 式中的声子频率ωq不是常数，而与温度有关：

    式中：ω(0)是T=0 K时石墨烯原子的振动频率；ε0，ε1和ε2分别是原子振动的简谐系数、第一和第二非简谐系数.考虑到自旋方向后，系统的电子与声子相互作用能为：

    将(12)式代入(9)式，得到考虑到原子非简谐振动和外延石墨烯电子系统的能量随序参量a，b，c，d和电子关联U，G的变化式.由BC，BZ和PM态的序参量，分别写出这三态能量的表示式EBC，EBZ和EPM，由相变时两相的能量相等，得到系统的相变曲线和系统的三相点.

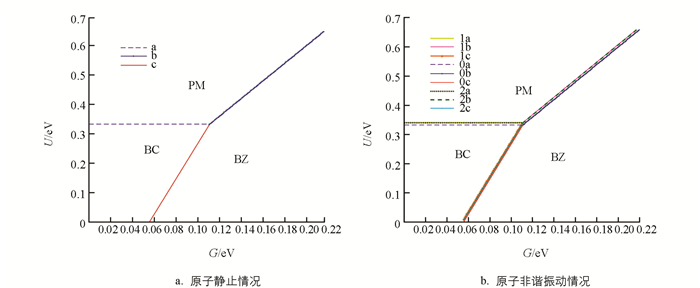
    对钨(W)基外延石墨烯作具体计算，得到的相图见图 7.其中，图 7a是原子静止的结果，而图 7b为原子作非简谐振动的结果[46].

    由图 7看出：金属基外延石墨烯发生半金属-反铁磁-顺磁态的相变取决于原子内部的电子关联U和原子间的电子关联G.当U=0.332 84 eV和G=0.119 04 eV时，才会出现半金属相、反铁磁相和顺磁相这三相共存.不考虑原子非简谐效应时，它的相图与温度无关；考虑原子作非简谐振动后，其相变曲线要上移，发生半金属-反铁磁-顺磁相变的条件要受温度的影响，低温下更易发生半金属-反铁磁-顺磁相变.

4.   三维PbO2材料拓扑相变与非简谐效应

    4.1.   PbO2拓扑材料结构相变的非简谐效应

  • 二氧化铅良好的导电性及稳定的化学惰性，早在20世纪30年代就被作为不溶性阳极用于化工工业生产中[47]，因其性能独特和应用广泛，国内外已对制备方法和应用进行不少研究[48]. 1979年文献[49]发现，其他二元金属氧化物(如TiO2，GeO2，SnO2)通常是半导体，而β-PbO2是一种高导电性的金属材料.虽然β-PbO2已被广泛应用了很长时间，但它本质上是金属还是半金属尚不清楚.此外，它的高电导率的起源仍不甚清楚.后来研究发现，PbO2是一种典型的、应用非常广泛的拓扑材料，文献[50]综述了国内外对它的研究情况，并用密度泛函理论基于第一原理，计算PbO2中非简谐波效应驱动的拓扑相变，证明非简谐性在结构相变中的重要作用，探索了非简谐效应的影响.目前研究情况见表 3.

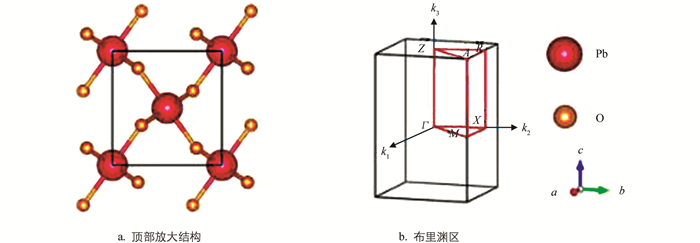
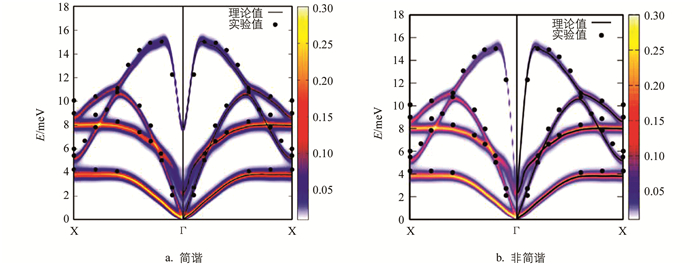
    文献[50]对PbO2的拓扑相结构进行研究，用谐波近似法对各相的声子谱进行计算分析表明：低温时为正交相，而高温时为四方相(β-PbO2).正交相为绝缘体，是非稳定的，它的结构的顶部放大结构见图 8a；四方相(β-PbO2)具有半金属性质，是稳定的，具有拓扑相结构，它的结构对应的布里渊区(BZ)见图 8b.

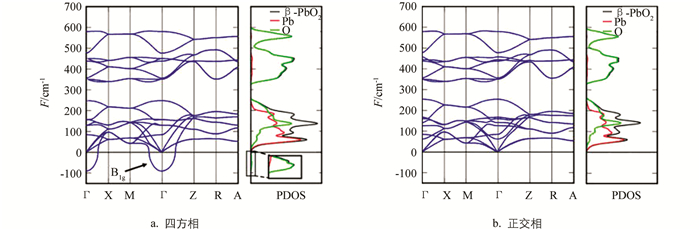
    图 9给出两种相结构的声子谱，图 9a为正交相沿高对称线的声子谱，图 9b为四方相(β-PbO2)沿高对称线的声子谱，表明β-PbO2的声子谱，有一个假想的频率B1g模式存在于Γ点.

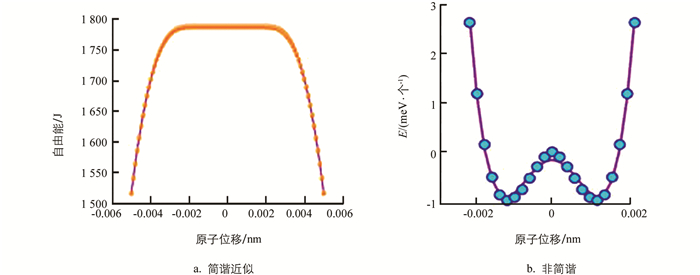
    文献[50]考虑到原子振动的非简谐效应，对四方结构的β-PbO2的自由能随位移的变化进行研究表明：在有限温度下，由于声子-声子相互作用，将使某些构型出现在势能表面的能量鞍点上.其中低于转变温度时，非简谐效应不突出，自由能随原子位移的变化不具有双阱结构(图 10a)，四方结构的β-PbO2是不稳定的；但温度较高时，非简谐效应突出，自由能随原子位移的变化具有双阱结构(图 10b)，结构由不稳定变为稳定，从平凡绝缘体变到半金属的一种拓扑相，即非简谐效应驱动了PbO2的结构转变.

    • 4.2.   SnTe热电材料结构相变的非简谐效应

  • 热电材料具有将热能转化为电能的能力，反之亦然.热电转化能力的高低由品质因数表征，品质因数越高，热电装置热电转化的效率就越高.增加品质因数的一种可能的策略是寻找导热系数小的材料，这意味着寻找声子-声子散射较大的系统，即声子谱中具有主导非简谐效应的系统，因此，用非微扰理论来处理非简谐性问题对于理解晶格动力学和材料的热电转化效率至关重要.在热电材料中，SnTe由于其具有一些有趣的性质而引起了人们的关注[60-61].它不仅有很高的品质因数，是一种有效的热电材料，更重要的是，在室温下它具有类NaCl结构，结构简单，非简谐效应明显，是验证非微扰理论方法解决非简谐性问题的理想材料.

    2018年，Guilherme等人利用随机自洽谐波近似(SSCHA)，使用QUANTUM-ESPRESSO软件包进行密度泛函理论计算，给出了SnTe的非简谐声子谱作为温度的函数[55, 62]，确定振动光谱和铁电转变的非简谐效应的大小.通过谐波声子色散分析得到，在环境压力下，SnTe在30~100 K温度范围内经历相变，低温下晶体对称性从立方(Fm3m)转变为菱形(R3m)，该畸变是一种置换相变，与区域中心的声子不稳定性相容.实际样品的SnTe是非化学计量的，铁电转变温度强烈地取决于系统中存在的孔穴数，温度为100 K时孔穴浓度约为1×1020 cm-3，温度下降到约30 K时孔穴浓度增大10倍.通过非简谐色散曲线实验数据分析，在100 K条件下得到SnTe沿BZ高对称方向，沿路径X-Γ-X的光谱函数见图 11.由图 11看出：上有LO/TO分裂，而下无LO/TO分裂.

    将利用自洽波近似自能计算得到的SnTe的非简谐声子色散与实验进行了比较，发现与实验数据有很好的一致性.为了进一步研究SnTe的二阶结构相变随温度T的变化情况，还计算了TO模在Γ点的能量平方，所得包含非简谐性的数据与X射线非弹性散射实验中T≈23 K铁电跃迁是一致的[52].

    这些结果表明：SnTe这种热电材料中的热电转变与非简谐效应的大小有关.

5.   晶体结构相变非简谐效应研究展望

  • 目前国内外尽管对晶体结构相变的非简谐效应进行了不少研究，但这些研究由于只考虑到原子振动的第一、二非简谐项，许多相变性质(如非简谐效应与相变温度的定量关系、相的稳定性等)随温度等的变化规律问题并未解决.目前有待进一步深入研究和改进处是：①除实验研究外，理论研究目前的主要方法是采用传统的固体物理方法和用密度泛函理论基于第一性原理等计算方法.传统的固体物理方法物理图像清晰，能体现物理变化过程，能确定物理性质随温度变化规律的解析式，但数学推导和计算较复杂；而密度泛函理论第一性原理等计算方法，能较快得到结果，但不能体现物理变化过程和物理性质随温度的变化规律.如何将两者有机结合，特别是与实验结合，是有待探索的重要问题；②晶体结构相变中的许多新的非简谐效应，不仅对实验仪器设备要求较高，而且对目前的非简谐理论提出了更高的要求，即不能仅停留于经典和半经典半量子理论和方法上.如何采用量子理论和方法，更深入研究不断出现的非简谐效应新现象和新规律，是有待探索的另一个重要问题.

Figure (11)  Table (3) Reference (62)

Catalog

    Copyright Journal of Southwest University Natural Science Edition

    Address： Tel：023-68254576, 68252540, 68366165,68366917 E-mail：lkxb@swu.edu.cn

    Supported by:Beijing Renhe Information Technology Co. Ltd

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return