Local Multi-granulation Covering-Based Rough Sets

将经典粗糙集理论扩展至多粒度空间下的粗糙集模型^[1-2]，在理论研究和实际应用上愈加重要，广泛应用于特征选择、知识获取、决策分析、模式识别和医疗诊断等领域^[3-6]. 因实际问题中数据的多样性，经典粗糙集在实际应用场景中具有局限性，各类粗糙集扩展模型的研究成为一个研究热潮，如：决策粗糙集模型、变精度粗糙集模型、概率粗糙集模型等^[7-9]. 文献[10]研究了多粒度粗糙集模型的代数结构. 文献[11]对模糊空间下的多粒度粗糙集模型进行了探讨. 文献[12]研究了覆盖空间下的多粒度粗糙集模型，且利用元素的最小描述对不同多粒度覆盖粗糙集进行比较，发现了乐观多粒度和悲观多粒度与平均多粒度覆盖粗糙集之间的关系. 文献[13]提出了基于模糊邻域多粒度粗糙集的特征选择算法，从信息的角度提出了基于模糊邻域熵的不确定性度量. 文献[14]提出了4类基于覆盖的乐观(悲观)多粒度模糊粗糙集模型，引入了模糊互补β-邻域簇的概念. 文献[15]研究了基于矩阵的动态优势多粒度粗糙集(DMGRSs)方法，更新了具有演化数据的动态有序信息系统中的多粒度近似. 随着大数据的发展，为了提升精确率，文献[16-17]提出了局部粗糙集模型，提出了决策理论粗糙集在大数据背景下目标概念近似表示的改进，以及局部多粒度决策粗糙集. 在局部粗糙集的基础上，文献[18]提出了基于不完备信息系统下的局部粗糙集理论，将局部粗糙集从完备信息系统扩展至不完备信息系统. 文献[16-18]的研究都基于等价关系. 文献[19]基于相容关系，探讨了乐观多粒度和悲观多粒度的局部相容粗糙集. 文献[20]研究了相似关系下的局部粗糙集模型. 本文从信息概念和存在概念之间的交叉角度，利用覆盖粗糙集理论基础^[21-25]，提出了一种在覆盖近似空间下的局部粗糙集模型：局部覆盖粗糙集，以及局部乐观多粒度覆盖粗糙集和局部悲观多粒度粗糙集. 本文探讨了在多粒度空间与单粒度空间下模型的内在联系，和局部多粒度覆盖粗糙集的基本性质，深入研究了对乐观多粒度和悲观多粒度下的局部多粒度覆盖粗糙集中上、下近似集的关系. 研究结果表明，局部多粒度覆盖粗糙集在特定情况下可退化为多粒度覆盖粗糙集模型，是对原有模型的有效拓展.

近似概念是覆盖近似空间中的知识表示. 文献[21]提出的多粒度覆盖粗糙集模型将多粒度的思想引入覆盖粗糙集模型中，采用一簇覆盖，提出了一种多粒度覆盖粗糙集模型. 本节介绍经典多粒度覆盖粗糙集的相关基础概念.

定义 1^[3-4]  设U为论域，C为U的子集簇，如果C中所有的集合均不为空，且有∪C=U，那么称C为U上的覆盖.

定义 2^[3]  设U为论域，C={C₁，C₂，…，C_n}为论域U上的覆盖，对于∀x∈U，x在覆盖近似空间〈U，C〉中的最小描述MdC(x)为

例 1  给定覆盖近似空间〈U，C〉，其中U={1，2，3，4，5，6，7，8，9}，C₁，C₂∈C，C₁={{1，2，4，5，7，8}，{2，5，8}，{3，5，6，9}}，C₂={{1，2，3}，{4，5，6，7，8}，{7，8，9}}. 最小描述和覆盖的近似集可以由以下计算得到：

根据定义2有

定义 3^[20]  设U为论域，C={C₁，C₂，…，C_n}为论域U上的覆盖，对于∀X∈U，X在覆盖近似空间〈U，C〉中的覆盖粗糙集下近似和覆盖粗糙集上近似分别为C(X)和C(X)：

该形式下的覆盖粗糙集将由最大描述和最小描述转化为粗糙集经典表示，当覆盖关系变成划分关系时，覆盖粗糙集即为经典粗糙集.

这里对文献[16]中提出的局部粗糙集的定义作基本介绍.

定义 4  令〈U，≼〉为偏序集，≼是论域中的一种偏序关系，对任意的x，y∈U，D(y/x)有：

(a) 0≤D(y/x)≤1；

(b) x≤y⇒D(y/x)=1；

(c) x≤y≤z⇒D(x/y)≤D(x/z).

其中$D(Y/X) = \frac{{|X \cap Y|}}{{|X|}}$为包含度，|X|表示集合X内的元素个数，同时有

定义 5^[16]  令(U，R)为一个近似空间，D是定义在P(U)×P(U)上的包含度，P(U)为论域U的幂集，则对任意∀X⊆U，有

〈R_α(X)，R_β(X)〉称为局部粗糙集，R_α(X)称为集合X的α-下近似集，R_β(X)称为集合X的β^-上近似集. 当且仅当α=1，β=0时，局部粗糙集就退化为经典粗糙集.

文献[21]提出的多粒度覆盖粗糙集模型，结合多重二元关系，将多粒度空间引入文献[10]所提出的覆盖粗糙集模型中，采用一簇而非单个的覆盖，提出了一种新的多粒度覆盖粗糙集模型. 以下是相关的基本介绍：

定义 6^[3]  在近似空间(U，C)上，C₁，C₂，…，C_m为该近似空间的一簇覆盖，对于∀X⊆U，X的乐观多粒度覆盖下近似集、上近似集分别记为$\underline {{L^{\sum\limits_{i = 1}^m {{C_i}} (X)}}} $和$\overline {{L_{\sum\limits_{i = 1}^m {{C_i}} (X)}}} $，有：

定理1   $\underline {\sum\limits_{i = 1}^m {{C_i}} (X)} = \bigcup\limits_{i = 1}^m {\underline {{C_i}} } (X), \sum\limits_{i = 1}^m {{C_i}} (X) = \bigcap\limits_{i = 1}^m {\overline {{C_i}} } (X)$

由上述结论可以得到多粒度覆盖上近似与覆盖上近似之间的关系，以及多粒度覆盖下近似与覆盖下近似之间的关系.

定义 7  在近似空间(U，C)上，C₁，C₂，…，C_m为该近似空间上的一簇覆盖，对于∀X⊆U，X的悲观多粒度覆盖下近似集、上近似集分别记为$\underline {{B^{\sum\limits_{i = 1}^m {{C_i}} (X)}}} $和$\overline {{B_{\sum\limits_{i = 1}^m {{C_i}} (X)}}} $，有：

定义 8^[21]  设U为论域，C1={C₁，C₂，…，C_n}和C2={C₁，C₂，…，C_m}为论域上的两个覆盖. ∀x⊆U，若对于∀Ci∈MdC1(x)，都存在Cj∈MdC2(x)，使得Cj⊆Ci，则称覆盖C2比覆盖C1细，记为C2≼C1. 若C2≼C1且C1≼C2，则称覆盖C2与覆盖C1相等，记为C2=C1；否则为不相等，记为C2≠C1. 若C2≼C1且C2≠C1，则称覆盖C2较覆盖C1严格细，记为C2$ \prec $C1.

定理 2^[21]  设U为论域，C1={C₁，C₂，…，C_n}和C2={C₁，C₂，…，C_m}为论域上的两个覆盖，若C2≼C1，则对∀X⊆U，有$\underline {C1} (X) \subseteq \underline {C2} (X)$和$\overline {C2} (X) \subseteq \overline {C1} (X)$.

本节提出一种新的粗糙集扩展模型：局部覆盖粗糙集. 并在此基础上扩展至多粒度空间，形成多粒度局部覆盖粗糙集. 讨论单粒度空间和多粒度空间下的局部覆盖粗糙集模型及其性质，并与覆盖粗糙集对比且加以说明.

定义 9 在近似空间(U，C)上，令U为论域，C={C₁，C₂，…，C_n}为该近似空间(论域)的一簇覆盖，对于∀X⊆U，0≤β＜α≤1，X在覆盖近似空间(U，C)中的局部覆盖粗糙集的下近似集、上近似集分别为：

其中，C_α(X)称为X的局部覆盖粗糙集α-下近似集，C_β(X)称为局部覆盖粗糙集β^-上近似集，其边界集为BN(X)=C_β(X)-C_α(X). 当BN(X)=Ø时，称X是可定义的，否则是不可定义的. 当且仅当α=1，β=0时，局部覆盖粗糙集退化为覆盖粗糙集，即：

这说明局部覆盖粗糙集并没有改变原有覆盖关系下的目标近似，与原有的覆盖粗糙集的近似表示一致.

例 2  在例1的假设条件下，令α=0.6，β=0.4，令X={1，2，5，8}，则局部覆盖粗糙集的上下近似集为：

根据定义8，可得X关于覆盖C₁的局部覆盖α-下近似集为$\begin{array}{*{20}{l}} {{{\underline {{C_1}} }_{\left( {0.{\rm{ }}6} \right)}}(X) = \left\{ {1{\rm{ }}, {\rm{ }}2, {\rm{ }}5{\rm{ }}, {\rm{ }}8} \right\}} \end{array}$，局部覆盖β-上近似集为$\begin{array}{*{20}{l}} {{{\overline {{C_1}} }_{\left( {0.{\rm{ }}4} \right)}}(X) = \left\{ {1{\rm{ }}, {\rm{ }}2, {\rm{ }}5{\rm{ }}, {\rm{ }}8} \right\}} \end{array}$.

所以，X关于覆盖C₂的局部覆盖α-下近似集为${\underline {{C_2}} _{\left( {0.6} \right)}}$(X)={1，2}，局部覆盖β-上近似集为${\overline {{C_2}} _{(0.4)}}(X) = \left\{ {1{\rm{ }}, {\rm{ }}2, {\rm{ }}5} \right\}$.

从上述计算结果看，

这表明对于集合X，其正域有增加，意味着在近似表示上可以更加精确. 而对于C₂，X在C₂的覆盖粗糙集上是完全不可定义的，但在C₂的局部覆盖粗糙集上可定义，表明对于集合X，局部覆盖粗糙集在知识近似表示方面是更精准的.

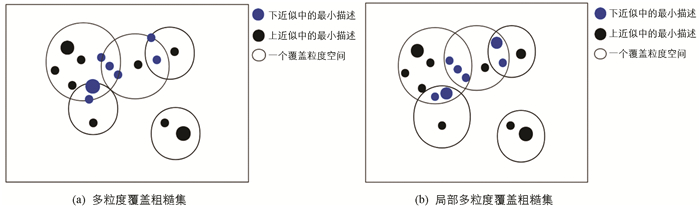
将单个粒度下的局部覆盖粗糙集扩展至多个粒度空间下得到的局部多粒度覆盖粗糙集. 而在多粒度近似空间中，多粒度覆盖粗糙集与局部多粒度覆盖粗糙集的表示见图 1.

其近似集定义表示及其性质的分析如下：

定义 10  在覆盖近似空间(U，C)上，U为论域，C={C₁，C₂，…，C_n}为论域上的一簇覆盖，对于∀X⊆U，0≤β＜α≤1，X在覆盖近似空间(U，C)上的局部乐观多粒度覆盖粗糙集的下、上近似集分别表示为：

定义 11  在覆盖近似空间(U，C)上，U为论域，C={C₁，C₂，…，C_n}为论域上的一簇覆盖，对于∀X⊆U，0≤β＜α≤1，X在覆盖近似空间(U，C)上的局部悲观多粒度覆盖粗糙集的下、上近似集分别表示为：

例 3  在例1的假设条件下，当X={1，2，5，8}时，根据定义6可计算覆盖C的乐观多粒度覆盖粗糙集的下近似集与上近似集：

根据定义10以及例2可得局部乐观多粒度覆盖粗糙集的下近似集、上近似集：

同理可求得悲观多粒度覆盖粗糙集的上、下近似集和局部悲观多粒度覆盖粗糙集的上、下近似集.

定理 3  设U为论域，C={C₁，C₂，…，C_n}为论域上的一簇覆盖，对于∀X⊆U，0≤β＜α≤1，有

证  对于∀x∈U，由局部多粒度覆盖粗糙集的下近似集可得：

而对于∀x∈U，根据局部多粒度覆盖粗糙集的上近似集可得：

证毕.

定理3说明了在覆盖近似空间中覆盖关系下的局部多粒度覆盖粗糙集的近似集与单粒度下的局部覆盖粗糙集之间的联系. 可以清晰地观察到：局部多粒度覆盖粗糙集的下近似集是所有单粒度下局部覆盖粗糙集下近似集的并集；局部多粒度覆盖粗糙集的上近似集是所有单粒度下局部覆盖粗糙集上近似集的交集.

定理 4  设U为论域，C={C₁，C₂，…，C_n}为论域上的一簇覆盖，对于∀X⊆U，0≤β＜α≤1，有：

(i) $\underline {{O^{\sum\limits_{i = 1}^n {{c_i}} {{(\mathit{\emptyset })}^\alpha }}}} = \mathit{\emptyset }, \overline {{O_{\sum\limits_{i = 1}^n {{C_i}} {{(\mathit{\emptyset })}^\beta }}}} = \mathit{\emptyset };\underline {{O^{\sum\limits_{i = 1}^n {{c_i}} {{(U)}^\alpha }}}} = U, \overline {{O_{\sum\limits_{i = 1}^n {{C_i}} {{(U)}^\beta }}}} = U;$

(ii) $\underline {{P^{\sum\limits_{i = 1}^n {{C_i}} {{(\mathit{\emptyset })}^a}}}} = \mathit{\emptyset }, \overline {P\mathop \sum \limits_{i = 1}^n {C_i}{{(\mathit{\emptyset })}^\beta }} = \mathit{\emptyset };\underline {{P^{\sum\limits_{i = 1}^n {{c_i}} {{(U)}^a}}}} = U, \overline {{P_{\sum\limits_{i = 1}^n {{C_i}} {{(U)}^\beta }}}} = U.$

定理 5  设U为论域，C={C₁，C₂，…，C_n}为论域上的一簇覆盖，对于∀X⊀U，有：

(i) 当α=1时，$\underline {{O^{\sum\limits_{i = 1}^n {{C_i}} {{(X)}^\alpha }}}} = \underline {{O^{\sum\limits_{i = 1}^n {{C_i}} (X)}}} , \underline {{P^{\sum\limits_{i = 1}^n {{c_i}} {{(X)}^\alpha }}}} = \underline {{P^{\sum\limits_{i = 1}^n {{C_i}} (X)}}} ;$；

(ii) 当β=0时，$\overline {{O_{\sum\limits_{j = 1}^n {{C_i}} {{(X)}^\beta }}}} = \overline {{O_{\sum\limits_{j = 1}^n {{C_i}} (X)}}} , \overline {{P_{\sum\limits_{i = 1}^n {{C_i}} {{(X)}^\beta }}}} = \overline {{P_{\sum\limits_{i = 1}^n {{C_i}} (X)}}} .$.

定理5表明了在特殊情况下，局部多粒度覆盖粗糙集会退化为多粒度覆盖粗糙集，以及两者在覆盖近似空间上的联系.

定理 6  设U为论域，C={C₁，C₂，…，C_n}为论域上的一簇覆盖，对于∀X⊆U，给定0≤β＜α≤1，下列结论不一定成立：

(i) $\underline {{O^{\sum\limits_{i = 1}^n {{C_i}} {{(X)}^\alpha }}}} \subseteq \overline {{O_{\sum\limits_{i = 1}^n {{C_i}} {{(X)}^\beta }}}} ;$；

(ii) $\underline {{P^{\sum\limits_{i = 1}^n {{C_i}} {{(X)}^\alpha }}}} \subseteq \overline {{P_{\sum\limits_{i = 1}^n {{C_i}} {{(X)}^\beta }}}} .$.

证  见例3. 限于篇幅，证明略.

定理6得出一个结论，即局部多粒度覆盖粗糙集在覆盖近似空间上不一定满足对偶性. 换一句话说，全局多粒度覆盖粗糙集中由下近似集的补，根据对偶性原理得到的其上近似集，在局部多粒度覆盖粗糙集中是不一定成立的.

定理 7  设U为论域，C={C₁，C₂，…，C_n}为论域上的一簇覆盖，若C₁≼C₂≼…≼C_n，且0≤α₁≤α₂≤…≤α_n，0≤β₁≤β₂≤…≤β_n，则

证  因为C₁≼C₂≼…≼C_n且0≤α₁≤α₂≤…≤α_n，所以根据定义7和定理1可推得

即

从而根据定理3有

同理，因为C₁≼C₂≼…≼C_n且0≤β₁≤β₂≤…≤β_n，根据定义7和定理1可得

即

根据定理3可得

证毕.

定理7说明：在给定的一簇覆盖中存在某种特殊的粗细关系，使得多粒度局部覆盖粗糙集的下近似与在最细条件下得到的局部覆盖粗糙集的下近似相等，多粒度局部覆盖粗糙集的上近似与在最细条件下得到的局部覆盖粗糙集的上近似也相等.

定理 8  设U为论域，C={C₁，C₂，…，C_n}为论域上的一簇覆盖，对于∀X⊆U，给定0≤β＜α≤1，有：

(i) $\underline {{P^{\sum\limits_{i = 1}^n {{C_i}} {{(X)}^\alpha }}}} \subseteq \underline {{O^{\sum\limits_{i = 1}^n {{C_i}} {{(X)}^\alpha }}}} ;$；

(ii) $\overline {{P_{\sum\limits_{i = 1}^n {{C_i}} {{(X)}^\beta }}}} \subseteq \overline {{O_{\sum\limits_{i = 1}^n {{C_i}} {{(X)}^\beta }}}} .$.

证  根据局部乐观多粒度覆盖粗糙集和局部悲观多粒度覆盖粗糙集的定义，定理8易证.

当下，多粒度粗糙集在粗糙集理论中的重要性愈加契合现实应用场景，新的理论和应用拓展可以有效推动粗糙集领域的发展. 本文在覆盖近似空间下，首先基于覆盖粗糙集中的最小描述转化后的粗糙集经典表示形式，提出了局部覆盖粗糙集，并研究了在多粒度近似空间下的局部乐观多粒度覆盖粗糙集和局部悲观多粒度覆盖粗糙集. 其次，研究了多粒度空间下的局部覆盖粗糙集与单粒度局部覆盖粗糙集间的内在联系，发现了局部多粒度覆盖粗糙集的上、下近似集跟所有单粒度下局部覆盖粗糙集的上、下近似集的代数关系. 最后，探讨了局部多粒度覆盖粗糙集与多粒度覆盖粗糙集间的一些基本性质，指出了局部多粒度覆盖粗糙集可在特定情况下由多粒度覆盖粗糙集泛化得到.