-
开放科学(资源服务)标志码(OSID):

-
概念是人类认知活动的基本单位,以概念为基础的粒计算方法是实现可解释性人工智能的途径之一[1-5]. 粒计算通过对复杂数据的多粒度化处理得以实现复杂问题的简易求解[6]. 多粒度化的数据呈现出大小不同的信息粒,从而构成了由小到大的粒度链条[7]. 在粒度链条中,小粒是构成大粒的基础,粒度的变化体现着思维过程的泛化和特化,在泛化和特化的双向思维驱动下,人们得以解决许多看似无法下手的困难问题[8-9].
形式概念分析(formal concept analysis,FCA)[10]是基于格论建立起来的数学方法,已经成为一种最有效的粒计算理论. 在应用的驱动下,根据实际需求可以通过各种方法构造不同类型的形式概念,包括经典形式概念、面向对象概念、面向属性概念、对偶概念等[11-14]. 最近十年,粗糙集、粒计算、模糊集、三支决策理论等推动了形式概念分析的发展,产生了许多有重要理论价值与应用价值的成果[15-20]. 其中,QI等[21]将三支决策理论(three-way decisions,3WD)中的三分思想引入形式概念分析,提出了三支概念分析(three-way concept analysis,3WCA). 具体就是通过在形式背景上定义负算子,刻画对象子集与属性子集间"共同不具有"的关系,并构造三支算子,将对象集或属性集三分,形成三支概念与三支概念格. 三支概念分析自2014年提出以来,得到了广泛的认可[22-24].
信息检索一直是人工智能的重要研究课题,但是,现有的信息检索方法广泛采用距离度量相似程度,不能完全客观精准地对具有家族相似性的原型范畴进行刻画. 如果能够采用粒计算思想,从概念的角度对整个粒度链条进行深入研究,特别是对粒度链条顶端的子格进行研究,或许可以得到满意的解决.
现代范畴理论[25-26]强调相似的传递性,使得看似不相关的对象通过相似的传递性联系在一起,形成一个个特定的范畴,在同一范畴内,成员共享"家族相似性". 显然,采用距离度量相似程度不能准确地刻画这样的情形. 为了解决这一问题,在现代范畴理论的启发下,智慧来与李逸楠首次提出了概念簇,用以刻画一组具有家族相似性的概念,并应用于相似对象的检索[27]. 概念簇中的概念包含了对象具有的共同属性,但忽略了对象都不具有的属性,不利于解决某些特定的问题.
为了解决上述问题,本文融合现代范畴理论与三支概念分析,提出了用三支概念簇刻画具有家族相似性的三支概念集合,并对三支概念簇的性质、运算以及应用进行了初步的探讨.
HTML
-
形式概念分析[10]建立在格论基础之上,对哲学中的概念进行了高度的数学概括,具有良好的性质,已经广泛应用于知识表示、数据挖掘、近似推理等诸多领域. 形式背景是领域本体的抽象描述,也是形式概念分析研究的具体对象和起点.
具体地,形式背景可以抽象为一个三元组K=(G,M,I),其中,G为对象集合,M为属性集合,且均非空有限,I为G和M之间的二元关系. 进一步,使用I(x,a)=1表示对象x具有属性a,使用I(x,a)=0表示对象x不具有属性a. 在下文中,为了方便起见,对于单元素集合,只列出其中的元素. 例如,用x表示集合{x}.
对于X⊆G和A⊆M,分别定义对象集和属性集上的算子如下:
若X*=A且A*=X,则称(X,A)是形式背景K的一个概念. 已经证明,形式背景K的全体概念构成一个完全格,并称之为概念格,记做L(K).
现代范畴理论[25-26]着重分析了家族相似概念,从理论上阐述了在同一个范畴中有可能存在一些不具有共同属性的对象. Wittgenstein通过深入了解许多不同类型的游戏,发现当中的一些游戏并不具有共同点,但是体现出了不可忽视的紧密联系. 经过分析得知,这些游戏是通过相似的传递性而密切联系在一起,利用这种密切联系,Wittgenstein将这些游戏划分成了多个家族. 语言学家Labov和Rosch在深入研究自然范畴的基础上,将"家族相似性"解释为家族成员具有某些相似之处,并将"原型范畴"(prototype category)解释为具有"家族相似性"的自然范畴,从而奠定了现代范畴理论的基础.
现代范畴理论的主要观点包括:
1) 范畴内的各个成员通过相似的传递性聚集在一起,所有成员不一定存在相同的约束;
2) 范畴中可能存在一个或多个中心,形成单一中心结构或多中心结构;
3) 对于一个范畴,最具典型性的成员位于范畴的中心.
现代范畴理论的主要观点在粒计算理论中已经有大量的体现. 在现代范畴理论的启发下,智慧来等提出了概念簇,用以刻画具有某些特定相似之处的概念,并应用于基于概念格的相似对象检索.
定义 1[27] 给定一个形式背景K=(G,M,I),X⊆G和A⊆M. 若
则称C(X,A)是K的一个概念簇.
文献[27]已经证明,概念簇本质上是概念格的子格,位于粒度链条的最顶端,使用概念簇代替子格,是为了强调概念之间的家族相似性,以便于概念格理论的应用.
-
三支概念分析[21-22]相比较于经典形式概念分析,刻画了对象共同不具有的属性,能够提供经典形式概念分析所不能提供的某些细节. 为了构造三支概念,首先需要定义对象集和属性集上的负算子.
给定一个形式背景K=(G,M,I),X⊆G,B⊆M,对象集和属性集上的负算子分别定义如下:
定义 2 给定一个形式背景K=(G,M,I),X⊆G,A,B⊆M,定义对象导出三支算子如下:
进一步,若
${X^ \triangleleft } = (A, B)且{(A, B)^ \triangleright } = X$ ,则称(X,(A,B))为对象导出三支概念,简称为OE-概念. 已经证明,形式背景K的全体对象导出三支概念构成一个完全格,并称之为对象导出三支概念格,记做OEL(K).在OEL(K)中存在一类对象诱导的三支概念,两类属性诱导的三支概念,这些概念在基于三支概念分析的应用中发挥着重要作用,具体定义如下.
定义 3 给定一个形式背景K=(G,M,I),x∈G,a∈M. 称(
$x^{\triangleleft \triangleright}, x^{\triangleleft}$ )为对象诱导的三支概念,称(a*,${a^{* \triangleleft }}$ )为Ⅰ型属性诱导的三支概念,称(a*,${a^{\bar * \triangleleft }}$ )为Ⅱ型属性诱导的三支概念.例 1 给定一个形式背景K=(G,M,I),如表 1所示,其中共包含4个对象和5个属性,用符号"×"表示某个对象具有某个属性. 形式背景K的对象导出三支概念格OEL(K),如图 1所示.
形式背景K的对象导出三支概念格OEL(K)中包含4个对象诱导的三支概念,分别为:对象1诱导的(1,(ace,bd)),对象2诱导的(2,(bd,ace)),对象3诱导的(3,(abe,cd))和对象4诱导的(4,(abcd,e)).
此外,OEL(K)中包含5个Ⅰ型属性诱导的三支概念,分别为:属性a诱导的(134,(a,Ø)),属性b诱导的(234,(b,Ø)),属性c诱导的(14,(ac,Ø)),属性d诱导的(24,(bd,e))和属性e诱导的(13,(ae,d)).
再者,OEL(K)中包含5个Ⅱ型属性诱导的三支概念,分别为:属性a诱导的(2,(bd,ace)),属性b诱导的(1,(ace,bd)),属性c诱导的(23,(b,c)),属性d诱导的(13,(ae,d))和属性e诱导的(24,(bd,e)).
1.1. 形式概念分析与概念簇
1.2. 三支概念分析
-
概念簇[27]建立于经典概念格的基础之上,只考虑了对象具有的共同属性. 然而,在许多情况下,不仅要考虑对象具有的共同属性,还需要考虑对象都不具有的属性. 在现代范畴理论的启发下,本文在三支概念分析的基础上提出三支概念簇.
-
本质上,概念簇刻画了一组具有家族相似性的概念. 在此基础上,我们提出三支概念簇,用以描述具有家族相似性的三支概念集合.
定义 4 给定一个形式背景K=(G,M,I),x∈G,a∈M. 若
则称t(x,a)为对象x和属性a诱导的Ⅰ型三支概念簇.
定义 5 给定一个形式背景K=(G,M,I),x∈G,a∈M. 若
则称t(x,a~)为对象x和属性a诱导的Ⅱ型三支概念簇.
性质 1 给定一个形式背景K=(G,M,I),x∈G,a∈M. 三支概念簇t(x,a)和t(x,a~)均是OEL(K)的子格.
证 首先,由形式背景K=(G,M,I)的有限性可知OEL(K)是有限的,进而可知t(x,a)是有限的. 其次,t(x,a)中存在唯一的最大元(a*,
${a^{* \triangleleft }}$ ),且存在唯一的最小元($x^{\triangleleft \triangleright}, x^{\triangleleft}$ ). 综上可知,三支概念簇t(x,a)是OEL(K)的一个子格.同理可证t(x,a~)也是OEL(K)的一个子格. 证毕.
定义 6 给定一个形式背景K=(G,M,I),x∈G,a∈M. 称t(x,Ø)为对象x诱导的三支概念簇,称t(Ø,a)为属性a诱导的Ⅰ型三支概念簇,称t(Ø,a~)为属性a诱导的Ⅱ型三支概念簇.
实际上,对于对象x和属性a诱导的Ⅰ型三支概念簇t(x,a),令a=Ø,即可得到对象x诱导的三支概念簇t(x,Ø);对偶地,令x=Ø,即可得到属性a诱导的Ⅰ型三支概念簇t(Ø,a).
对于对象x和属性a诱导的Ⅱ型三支概念簇t(x,a~),令x=Ø,即可得到属性a诱导的Ⅱ型三支概念簇t(Ø,a~).
例开 2 对于例1中的形式背景K,考察其上的三支概念簇如下.
形式背景K中包含4个对象诱导的三支概念簇,分别为:
对象1诱导的t(1,Ø)={(1,(ace,bd)),(13,(ae,d)),(14,(ac,Ø)),(134,(a,Ø)),(1234,(Ø,Ø))};
对象2诱导的t(2,Ø)={(2,(bd,ace)),(23,(b,c)),(24,(bd,e)),(234,(b,Ø)),(1234,(Ø,Ø))};
对象3诱导的t(3,Ø)={(3,(abe,cd)),(13,(ae,d)),(23,(b,c)),(34,(ab,Ø)),(134,(a,Ø)),(234,(b,Ø)),(1234,(Ø,Ø))};
对象4诱导的t(4,Ø)={(4,(abcd,e)),(14,(ac,Ø)),(24,(bd,e)),(34,(ab,Ø)),(134,(a,Ø)),(234,(b,Ø)),(1234,(Ø,Ø))}.
形式背景K中包含5个属性诱导的Ⅰ型三支概念簇,分别为:
属性a诱导的t(Ø,a)={(134,(a,Ø)),(34,(ab,Ø)),(14,(ac,Ø)),(13,(ae,d)),(3,(abe,cd)),(1,(ace,bd)),(4,(abcd,e)),(Ø,(abcde,abcde))};
属性b诱导的t(Ø,b)={(234,(b,Ø)),(23,(b,c)),(34,(ab,Ø)),(24,(bd,e)),(2,(bd,ace)),(3,(abe,cd)),(4,(abcd,e)),(Ø,(abcde,abcde))};
属性c诱导的t(Ø,c)={(14,(ac,Ø)),(1,(ace,bd)),(4,(abcd,e)),(Ø,(abcde,abcde))};
属性d诱导的t(Ø,d)={(24,(bd,e)),(2,(bd,ace)),(4,(abcd,e)),(Ø,(abcde,abcde))};
属性e诱导的t(Ø,e)={(13,(ae,d)),(3,(abe,cd)),(1,(ace,bd)),(Ø,(abcde,abcde))}.
形式背景K中包含5个属性诱导的Ⅱ型三支概念簇,分别为:
属性a诱导的t(Ø,a~)={(2,(bd,ace)),(Ø,(abcde,abcde))};
属性b诱导的t(Ø,b~)={(1,(ace,bd)),(Ø,(abcde,abcde))};
属性c诱导的t(Ø,c~)={(23,(b,c)),(3,(abe,cd)),(2,(bd,ace)),(Ø,(abcde,abcde))};
属性d诱导的t(Ø,d~)={(13,(ae,d)),(1,(ace,bd)),(3,(abe,cd)),(Ø,(abcde,abcde))};
属性e诱导的t(Ø,e~)={(24,(bd,e)),(4,(abcd,e)),(2,(bd,ace)),(Ø,(abcde,abcde))}.
-
三支概念簇是具有家族相似性的三支概念集合,三支概念簇的运算在本质上是集合的运算,首先给出三支概念簇的运算性质.
性质 2 给定一个形式背景K=(G,M,I),x∈G,a∈M. 以下命题成立:
1)
$t(x, a) = t(x, \emptyset ) \cap t(\emptyset , a);$ 2)
$t\left( {x, {a^ \sim }} \right) = t(x, \emptyset ) \cap t\left( {\emptyset , {a^ \sim }} \right).$ 证 1) 一方面,t(x,Ø)由OEL(K)中所有大于等于(
$x^{\triangleleft \triangleright}, x^{\triangleleft}$ )且小于等于(G,$G^{\triangleleft}$ )的三支概念组成. 另一方面,t(Ø,a)由OEL(K)中所有大于等于(Ø,${\emptyset ^ \triangleleft }$ )且小于等于(a*,${a^{* \triangleleft }}$ )的三支概念组成. 综合两个方面,由t(x,a)的定义可知t(x,a)=t(x,Ø)∩t(Ø,a). 命题1)成立.2) 同理可证命题2成立,证毕.
性质2实际上给出了利用对象诱导和属性诱导的三支概念簇计算任意三支概念簇的方法. 例如,考虑例2中的三支概念簇,利用性质2及例2的计算结果可得:
t(1,a)=t(1,Ø)∩t(Ø,a)={(1,(ace,bd)),(13,(ae,d)),(14,(ac,Ø)),(134,(a,Ø)),(1234,(Ø,Ø))}∩{(134,(a,Ø)),(34,(ab,Ø)),(14,(ac,Ø)),(13,(ae,d)),(3,(abe,cd)),(1,(ace,bd)),(4,(abcd,e)),(Ø,(abcde,abcde))}={(1,(ace,bd)),(13,(ae,d)),(14,(ac,Ø)),(134,(a,Ø))}.
性质 3 给定一个形式背景K=(G,M,I),x∈G,a∈M. 以下命题成立:
1) 若I(x,a)=0,则t(x,a)=Ø;
2) 若I(x,a)=1,则t(x,a~)=Ø;
3)
$OEL(K) = \left( {\bigcup\limits_{x \in G} t (x, \emptyset )} \right) \cup \left( {\emptyset , {\emptyset ^ \triangleleft }} \right);$ ;4)
$OEL(K) = \left( {\bigcup\limits_{a \in M} t (\emptyset , a) \cup t\left( {\emptyset , {a^ \sim }} \right)} \right) \cup \left( {G, {G^ \triangleleft }} \right).$ .证 1) 若I(x,a)=0,则概念
$\left( {{x^{ \triangleleft \triangleright }}, {x^ \triangleleft }} \right)$ 与$\left( {{a^*}, {a^{* \triangleleft }}} \right)$ 是不可比的,所以OEL(K)中不存在大于等于$\left( {{x^{ \triangleleft \triangleright }}, {x^ \triangleleft }} \right)$ 且小于等于$\left( {{a^*}, {a^{* \triangleleft }}} \right)$ 的概念,根据t(x,a)的定义可得t(x,a)=Ø. 命题1)成立.2) 同理可证命题2成立.
3) 若t(x,Ø)中的最小元与最大元分别为
$\left( {{x^{ \triangleleft \triangleright }}, {x^ \triangleleft }} \right)$ 和$\left( {G, {G^ \triangleleft }} \right)$ ,则$\bigcup\limits_{x \in G} t (x, \emptyset )$ 即为OEL(K)中大于等于所有对象诱导的且小于等于$\left( {G, {G^ \triangleleft }} \right)$ 的三支概念. 因此易得$OEL(K) = \left( {\bigcup\limits_{x \in G} t (x, \emptyset )} \right) \cup (\emptyset , \left. {{\emptyset ^ \triangleleft }} \right)$ . 命题3成立.4) 同理可证命题4成立,证毕.
需要指出的是,
$OEL(K) = \left( {\bigcup\limits_{a \in M} t (\emptyset , a)} \right) \cup \left( {G, {G^ \triangleleft }} \right)$ 与$OEL(K) = \left( {\bigcup\limits_{a \in M} t \left( {\emptyset , {a^ \sim }} \right)} \right) \cup \left( {G, {G^ \triangleleft }} \right)$ 均不一定成立.在例2中,
$OEL(K) = \left( {\bigcup\limits_{a \in M} t (\emptyset , a)} \right) \cup \left( {G, {G^ \triangleleft }} \right)$ 成立,但$OEL(K) = \left( {\bigcup\limits_{a \in M} t (\emptyset , {a^ \sim })} \right) \cup \left( {G, {G^ \triangleleft }} \right)$ 不成立. 实际上,$OEL(K) = \left( {\bigcup\limits_{a \in M} t (\emptyset , {a^ \sim })} \right) \cup \left( {G, {G^ \triangleleft }} \right) \cup (134, (a, \emptyset )) \cup (234, (b, \emptyset )) \cup (14, (ac, \emptyset ) \cup (34, (ab, \emptyset ))$ .
2.1. 三支概念簇的定义
2.2. 三支概念簇的性质
-
在信息检索的过程中,经常会请求系统推荐一类和某种已知对象类似,且具有或不具有某些特殊限定的对象. 如在网上购物系统中,顾客通常会要求客服进行产品的合理推荐,如:"请给我推荐一款与2号模特上身穿的相似,并且是深蓝色的,但不含拉链的外套",这种需求可以形式化地表述为:用G表示对象的集合,M表示属性的集合,在G中查找与对象x相似,且具有属性a,但不具有属性b的对象.
基于以上讨论,下面提出算法1以实现符合特定约束条件下的相似对象检索.
算法 1 基于三支概念簇的相似对象查找算法.
输入:形式背景K=(G,M,I),对象x∈G,属性a,b∈M.
输出:与对象x相似,且具有属性a,但不具有属性b的所有对象.
步骤1:建立形式背景K的对象导出三支概念格OEL(K);
步骤2:计算三支概念簇t(Ø,a)与t(Ø,b~);
步骤3:计算t(Ø,a)∩t(Ø,b~),并记其中全体对象诱导的三支概念的外延为集合E;
步骤4:从概念
$\left( {{x^{ \triangleleft \triangleright }}, {x^ \triangleleft }} \right)$ 开始,逐层遍历其父概念:记当前遍历的概念为(X,(A,B));
若X∩E≠Ø,则X∩E中包含的对象即为所求.
步骤5:返回结果,算法结束.
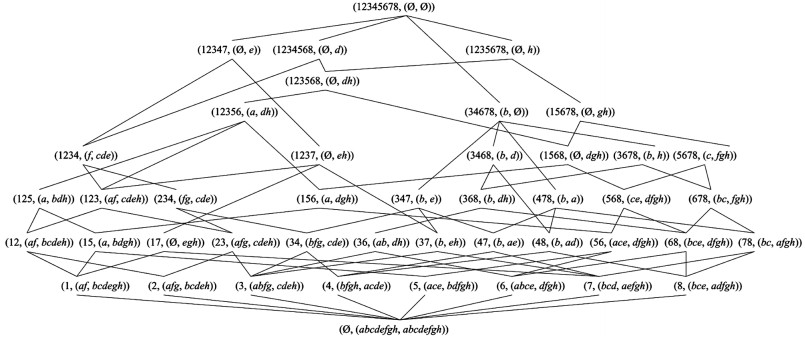
例 3 表 2描述了一个由8种生物构成的形式背景,也就是在形式概念分析理论研究中广为熟知的"生物和水"形式背景,其对象导出三支概念格如图 2所示. 由于所有的生物都需要水,这里不再考虑"需要水"这个生物属性,只考虑其余的8种生物属性. 用数字1到8分别代表蚂蝗、鱼、蛙、狗、水草、芦苇、豆与玉米. 另外,用小写字母a到h表示8种生物属性,即:在水中生活、在陆地生活、有叶绿素、双子叶、单子叶、能运动、有四肢与会哺乳.
为了更好地说明上述提出的基于三支概念簇的相似对象查找算法,我们将通过实际案例来进一步对基于概念簇和三支概念簇的相似对象查找算法进行分析对比.
首先,使用上述算法1,查找和芦苇(对象6)相似,且有叶绿素(具有属性c),但不能在陆地生活(不具有属性b)的生物.
输入:"生物和水"形式背景,对象6∈G,属性c,b∈M.
输出:与对象6相似,且具有属性c,但不具有属性b的所有对象.
步骤1:建立"生物和水"形式背景的对象导出三支概念格,如图 2所示;
步骤2:计算三支概念簇t(Ø,c)={(Ø,(abcdefgh,abcdefgh)),(5,(ace,bdfgh)),(6,(abce,dfgh)),(7,(bcd,aefgh)),(8,(bce,adfgh)),(56,(ace,dfgh)),(68,(bce,dfgh)),(78,(bc,afgh)),(568,(ce,dfgh)),(678,(bc,fgh)),(5678,(c,fgh))},t(Ø,b~)={(Ø,(abcdefgh,abcdefgh)),(1,(af,bcdegh)),(2,(afg,bcdeh)),(5,(ace,bdfgh)),(12,(af,bcdeh)),(15,(a,bdgh)),(125,(a,bdh))};
步骤3:计算t(Ø,c)∩t(Ø,b~)={(Ø,(abcdefgh,abcdefgh)),(5,(ace,bdfgh))},并记其中全体对象诱导的三支概念的外延为集合E={5};
步骤4:从概念
$\left( {{x^{ \triangleleft \triangleright }}, {x^ \triangleleft }} \right)$ =(6,(abce,dfgh))开始,逐层遍历其父概念:遍历其第一层父概念得到(56,(ace,dfgh))与(68,(bce,dfgh)),由{5,6}∩{5}={5}≠Ø可知对象5满足算法要求;由{68}∩{5}=Ø可知不满足算法要求,舍弃;综上可得,对象5即为所求.
步骤5:返回结果对象5,即符合条件的生物是水草,算法结束.
接下来,使用文献[27]所提出的基于对象直观图与概念簇的相似对象查找算法,查找和芦苇(对象6)相似,且有叶绿素(具有属性c),但不能在陆地生活(不具有属性b)的生物.
输入:"生物和水"形式背景,对象6∈G,属性c,b∈M.
输出:与对象6相似且具有属性c的所有对象.
步骤1:建立"生物和水"形式背景的对象直观图与概念格,见文献[27];
步骤2:在步骤1的对象直观图中查找大于等于(6,6*)的所有二元组,可得最大二元组仍为(6,6*);
步骤3:计算AC(6,c)=C(6**,c**)={(6,abce),(56,ace),(68,bce),(568,ce),(678,bc),(5678,c)};
步骤4:对于AC(6,c)中存在的概念(56,ace)=(5**,5*)和(68,bce)=(8**,8*),可得符合条件的对象为5和8;
步骤5:返回结果对象5和对象8,即符合条件的生物是水草和玉米,算法结束.
综上所述,针对同一个案例,对比两个算法可知,使用基于对象直观图与概念簇的算法只能检索和芦苇(对象6)相似且有叶绿素(具有属性c)的生物,无法检索其中不能在陆地生活(不具有属性b)的生物,即属性b无法被按需使用,最终得到的结果是水草(对象5)和玉米(对象8). 虽然此算法得到两种结果,但是根据常识可知,算法1得到的结果水草和基于对象直观图与概念簇的算法得到的结果之一玉米相比较更加符合条件. 因此,三支概念簇相比较于概念簇,更加有利于检索到符合需求的对象.
通过深入思考发现,三支概念簇之所以更加有利于检索到符合需求的对象,原因在于三支概念不仅考虑了对象共同具有的属性,而且还考虑了对象共同不具有的属性,使得三支概念比经典形式概念能够捕捉到更加精确的对象细节,从而发现更加细致的对象分类,检索到更加贴切实际应用场景的相似对象.
-
本文融合现代范畴理论与三支概念分析,提出了三支概念簇. 研究结果表明,三支概念簇刻画了具有"家族相似性"的三支概念集合,是检索符合特定约束条件下相似对象的有力工具. 三支概念簇作为三支概念分析中的重要粒度之一,还有许多值得深入探讨的问题. 例如:模糊形式背景下的模糊概念簇如何定义,与经典二值形式背景下的三支概念簇有何区别与联系;在动态环境下,三支概念簇如何更新;对于大规模形式背景,如何提高三支概念簇的计算效率. 最后,需要指出的是概念簇建立在形式概念的基础之上,构造概念格的复杂性限制了其大规模应用的有效性. 因此,如何采用新的思路,从新的角度研究概念簇还需要付出更多的努力.







 DownLoad:
DownLoad: