-
压缩感知理论是建立在矩阵分析、统计概率、优化与运筹学、泛函分析等理论基础上的信息采样与重构的理论[1-2].压缩感知是利用信号的稀疏表示,对信号进行有效压缩采样,通过压缩采样与非线性重构算法完美地重构信号.这一理论为信号恢复带来了新的处理方法,被广泛应用于医学成像、雷达探测、无线通信等诸多领域[3-5].在信号x∈
$\mathbb{R}$ n稀疏或近似稀疏的条件下,压缩感知理论转化为如下欠定线性模型:其中:y∈
$\mathbb{R}$ m为观测信号,A∈$\mathbb{R}$ m×n(m < < n)为测量矩阵,x∈$\mathbb{R}$ n为待重构的信号.实际观测中,加性噪音v时常影响信号y,上述压缩感知模型常转化为下述模型:此外,实际应用中测量矩阵常常受外界测量或其他因素的影响,导致测量矩阵A受扰动矩阵E的影响,即实际测量矩阵
$\mathit{\boldsymbol{\widehat A}} = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{E}}$ ,其中A称为理想测量矩阵.本文将扰动矩阵E与加性噪音v同时存在的压缩感知问题称之为完全扰动问题[6-7],该问题对应的模型为:从欠定线性模型中求解一个最稀疏的解是压缩感知的核心问题,该问题实际上是一个l0问题.由于l0问题在多项式时间内不能有效求解[8],文献[9]研究了如下l1完全扰动问题:
其中ε′A,K,y为全噪音参数.文献[9]中研究了信号鲁棒重构的限制等容条件(restricted isometrics property,RIP).信号重构条件为压缩感知的发展提供了重要研究意义.
在实际应用中,自然信号的结构丰富多彩.非零元素以块的结构方式出现的信号称为块稀疏信号[10],例如DNA-微阵列[11]、彩色图像处理[12]和源定位[13]等.块稀疏压缩感知实际是单独处理重构信号的每一小块.块稀疏压缩感知使块信号重构与采样的速度更快,且占用存储空间更少.若块稀疏信号用数学模型来表示,则在分块
$\mathscr{I}$ ={d1,…,dN}给定情况下,可以将任意向量x∈$\mathbb{R}$ n描述为如下形式相应地,测量矩阵A∈
$\mathbb{R}$ n×N也可以描述为如下形式其中向量x的第i个子块为x[i],第i块的大小为di.如果在给定分块
$\mathscr{I}$ 下,信号x至多有K个非零块,即$||\mathit{\boldsymbol{x}}|{|_{2, 0}} = \sum\limits_{i = 1}^N I \left({||\mathit{\boldsymbol{x}}[i]|{|_2}} \right) \le K$ ,则称x为块K稀疏信号,其中I(·)表示指示函数[14].实际上,当di=1(i=1,…,N)时,块稀疏信号x为传统稀疏信号.此外,信号x的$\frac{{{\mathit{\boldsymbol{l}}_2}}}{{{\mathit{\boldsymbol{l}}_1}}}$ 范数$||\mathit{\boldsymbol{x}}|{|_{2, 1}} = \sum\limits_{i = 1}^N I ||\mathit{\boldsymbol{x}}[i]|{|_2}$ ;信号x的$\frac{{{\mathit{\boldsymbol{l}}_2}}}{{{\mathit{\boldsymbol{l}}_\infty }}}$ 范数‖x‖2,∞=max{‖x[1]‖2,…,‖x[N]‖2};规定信号x的范数‖x‖2,2=‖x‖2.实际上,在稀疏信号的重构中,测量矩阵要求满足限制性等容条件或相干性等重构条件.特别地,在不引起混淆的情况下,本文记矩阵A的块限制等容常数δBK=δK.为了重构块稀疏信号,文献[15]引入了
$\mathit{\boldsymbol{\widehat A}}$ 的块限制性等容条件(BRIP).设测量矩阵A的块限制性等容常数为δK(K=1,2,…),εA(K)为相对误差上限,且$\frac{{||\mathit{\boldsymbol{E}}||_2^{(K)}}}{{||\mathit{\boldsymbol{A}}||_2^{(K)}}} \le \varepsilon _A^{(K)}$ ,若${\hat \delta _{K, \max }} = \left({1 + {\delta _K}} \right){\left({1 + \varepsilon _\mathit{\boldsymbol{A}}^{(K)}} \right)^2} - 1$ ,对于任意块K稀疏信号x∈$\mathbb{R}$ n,矩阵$\mathit{\boldsymbol{\widehat A}}$ =A+E的块限制性等容常数(BRIC)为满足的最小常数
${\hat \delta _K} \le {\hat \delta _K}, \max $ ,则称矩阵$\mathit{\boldsymbol{\widehat A}}$ 满足块限制性等容条件(BRIP).类似于文献[9],有如下不等式成立:通过研究l1问题,学者获得了大量的充分条件:文献[16]得到了信号重构的RIPδ2k < 0.453 1;文献[17]将RIP重构条件放松为δ2k < 0.465 2;文献[18]将RIP改进为
${\delta _{2k}} < \frac{{\sqrt 2 }}{2}$ .压缩感知的重构理论与重构算法具有重要的应用价值[19-22].
本文借鉴文献[22]延展了一类完全扰动的块压缩感知问题.令噪音上界为l2范数与
$\frac{{{\mathit{\boldsymbol{l}}_2}}}{{{\mathit{\boldsymbol{l}}_\infty }}}$ 范数,其问题具体形式可分别表示为如下形式:其中ε″A,K,y=‖A‖2(1+εA)ε′A,K,y.近年来压缩感知基本是以RIP为理论基础,但是验证RIP理论是一个在多项式时间内不能有效解决的问题,因此,利用RIP理论获得的结论,在实际应用中很难实行.本文针对问题(5),建立了处理块稀疏信号的扰动BOMP算法,根据扰动BOMP算法建立了各项仿真实验,验证了扰动BOMP算法的鲁棒性和稳定性.
HTML
-
本文考虑了理想测量矩阵A受扰动矩阵E的影响,即实际测量矩阵
$\mathit{\boldsymbol{\widehat A}}$ =A+E.对于扰动矩阵E与加性噪音v同时存在的块压缩感知问题,称为完全扰动的块压缩感知问题.此外,本文给出了完全扰动的块压缩感知问题的完全扰动块正交匹配追踪(BOMP)算法.对于完全扰动的块压缩感知问题(5),求解测量矩阵$\mathit{\boldsymbol{\widehat A}}$ 与残差向量rk-1的最强相关列λk:其中Λk表示第k次标签集.通过最小二乘法估计最小化问题的解
下面介绍完全扰动的BOMP算法具体迭代过程:
-
重构算法是压缩感知理论中的关键环节,本文从不同的角度建立了一系列数值仿真实验,研究了完全扰动的BOMP算法的重构性与有效性.为了保证算法的有效性,模拟实验对块稀疏信号采用均匀分块,即di=d(i=1,…,N).实验采用随机高斯矩阵作为测量矩阵A(A∈
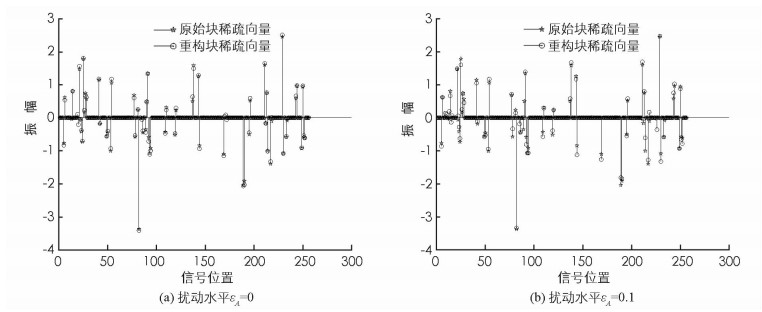
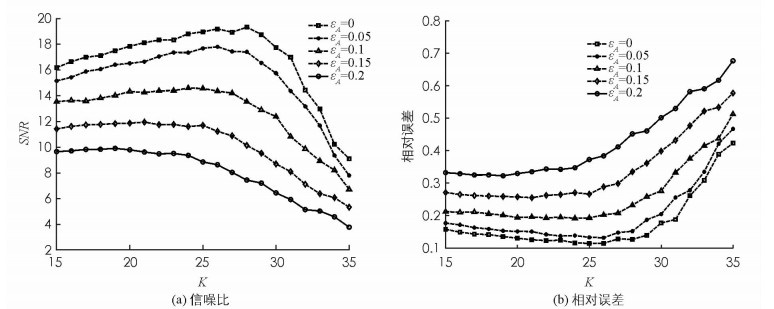
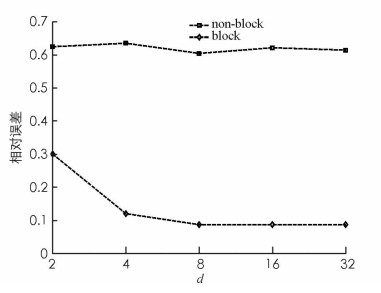
$\mathbb{R}$ 128×256),设定采样数m=128,信号维度n=256,扰动矩阵‖E‖2=εA‖A‖2且E中的元素服从正态分布,测量矩阵$\mathit{\boldsymbol{\widehat A}}$ =A+E,测量$\mathit{\boldsymbol{\widehat y}}$ =$\mathit{\boldsymbol{\widehat A}}$ x+v.假设块稀疏信号x中的元素服从标准正态分布,噪音v为高斯噪音.实验中扰动BOMP算法的重构性能运用相对误差$\frac{{{{\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^*}} \right\|}_2}}}{{{{\left\| \mathit{\boldsymbol{x}} \right\|}_2}}}$ (x*表示重构信号,x表示原始信号)以及信噪比SNR=20 log10$\left({\frac{{{{\left\| \mathit{\boldsymbol{x}} \right\|}_2}}}{{{{\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^*}} \right\|}_2}}}} \right)$ 来刻画.数值仿真实验在CPU为Intel奔腾i5-4300U(2.49 GHz),内存为4GB的电脑上运行,运行软件为MATLAB 7.14(R2012a).为了让实验结果更加准确,所有实验以独立重复200次的平均值作为最终统计结果.为了说明扰动BOMP算法的重构效果,在扰动水平分别为εA=0与εA=0.1下,图 1呈现了扰动BOMP算法的重构信号x*和原始信号x. 图 1描述了扰动BOMP算法的重构效果,该实验说明原始信号x的重构效果理想.此外,图 1也表明了扰动水平εA=0.1比εA=0重构效果略差,说明扰动BOMP算法的重构性能受扰动水平影响.因此,为了更为详细说明扰动水平对扰动BOMP算法的影响情况,首先将信号均分为128块,扰动水平分别取0,0.05,0.1,0.15,0.2. 图 2分别对块稀疏度从15到35变化的信号的信噪比以及相对误差进行了重构效果比较.从图 2可以看出:扰动水平越大,重构效果越差.此外,图 3表明运用扰动BOMP算法处理块稀疏信号的重构误差比扰动OMP算法更低,说明信号结构对于信号恢复至关重要.
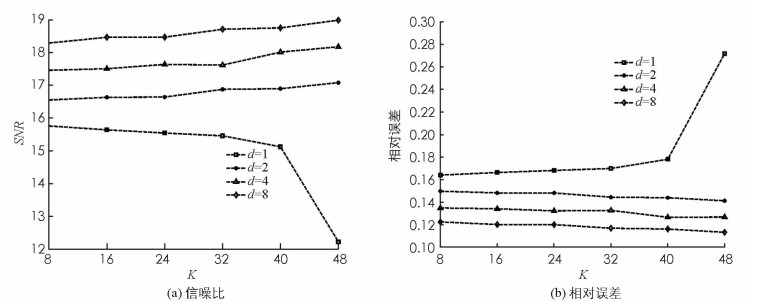
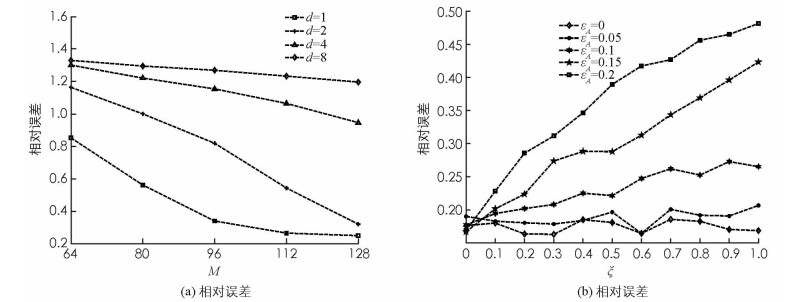
与扰动OMP算法的重构效果比较接下来,考虑块稀疏度与分块数对扰动BOMP算法的影响.在扰动水平εA=0.1时,信号的块大小d分别取1,2,4,8,图 4分别对信号的信噪比以及相对误差进行了重构效果比较. 图 4表明当块稀疏度从8到48变化时,块大小d均为2,4,8,曲线变化趋势不明显,即重构误差受块稀疏度影响较小.显然块大小d越大,重构效果越好.另外,在扰动水平εA=0.1时,信号的块大小d分别取1,2,4,8,图 5(a)中描述了信号采样数从64到128变化的相对误差变化趋势.显然,不管块大小d取1,2,4,8中的哪个值,采样越多,信号重构的误差越低,即采样数能有效降低信号重构误差.本文随机选取了矩阵A的部分或全部元素进行了扰动,其中测量矩阵A的元素部分扰动比例分别为0%,10%,20%,…,100%,探讨了部分扰动对扰动BOMP算法的重构效果的影响. 图 5(b)是部分扰动与相对误差的关系图,其中ξ表示矩阵A中元素部分扰动的比例.当εA=0时,矩阵A中元素扰动的比例ξ越小,信号重构误差越小.显然,扰动水平、部分扰动、分块数或采样数影响扰动BOMP算法的信号重构效果,且当扰动水平越低、部分扰动元素越少、分块数越小或采样数越多时,扰动BOMP算法重构信号的相对误差越小,即块稀疏信号重构效果越好.
-
本文利用完全扰动块压缩感知重构理论,运用数值仿真实验,研究了扰动水平、部分扰动、分块数以及采样数对扰动BOMP算法的重构性能的影响.实验表明:当扰动水平越低、部分扰动元素越少、分块数越小或采样数越多时,重构信号的相对误差越小,扰动BOMP算法能更加有效处理块稀疏信号.






 DownLoad:
DownLoad: