Dynamic Analysis of Smoking Transmission Model

本文基于吸烟者的特点，将种群分为潜在吸烟者、被动吸烟者、主动吸烟者与戒烟者.根据吸烟的传播特点，本文作如下假设和说明：

1) 假设被动吸烟是主动吸烟者与潜在吸烟者通过有效接触形成.

2) 考虑被动吸烟者与主动吸烟者之间的两种传播方式：

其一是被动吸烟者通过与每一个主动吸烟者接触从而变为主动吸烟者；另一种是被动吸烟者通过烟草行业大量的广告以及社会媒介等影响因素转变为主动吸烟者.

3) 考虑戒烟不彻底从而返回到潜在吸烟者.

建立模型如下：

其中：S，I₁，I₂，R分别表示t时刻潜在吸烟者、被动吸烟者、主动吸烟者以及戒烟者的数量；β表示潜在吸烟者与主动吸烟者的传播接触率系数；μ表示自然死亡率；σ表示由被动吸烟者转化为主动吸烟者的转化率；α表示被动吸烟者与主动吸烟者的传播接触率系数；γ表示戒烟率；δ表示为戒烟不成功又再次成为潜在吸烟者的比率.所有的变量是非负的，参数是正的.

系统(1)的可行域为

系统(1)存在无烟平衡点.利用下一代生成矩阵^[10]，计算出系统(1)的基本再生数为：

设系统(1)存在正(吸烟)平衡点E^*=(S^*，I₁^*，I₂^*，R^*)，则E^*满足

可得

且I₂^*满足：

其中

通过分析，有以下结论：

定理1  1) 当R₀>1时，系统(1)有一个正平衡点.

2) 当R₀ < 1时

(ⅰ) 当B < 0时，系统(1)没有正平衡点；

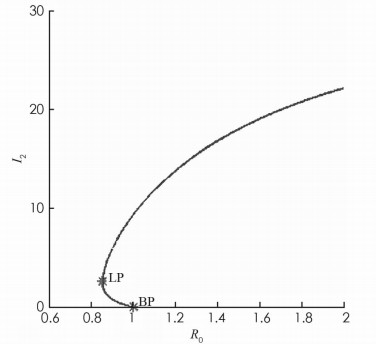
(ⅱ) 当B>0时，若B²=4AC，则有一个正平衡点，若B²>4AC，则有两个正平衡点(如图 1所示).

由定理1可知，当R₀ < 1时，系统(1)可能存在正平衡点.这意味着，系统可能会发生后向分支.下面应用文献[11]中的方法，分析系统(1)后向分支的存在性.

考虑R₀=1，我们选择β^*=β作为分支参数，则有

定义S=x₁，I₁=x₂，I₂=x₃，R=x₄.系统(1)变为：

系统在无烟平衡点的雅可比矩阵为

系统有特征值λ₁=0，λ₂=-μ，λ₃=-(μ+δ)，λ₄=-(2μ+σ+γ)，因此，零特征值相关的右特征向量为w=(w₁，w₂，w₃，w₄)^T，其中

对应的左特征向量为v=(v₁，v₂，v₃，v₄)，其中

选取v₃使v·w=1，则有

因此，b>0，当

时，a>0.系统出现后向分支(图 1)，即有以下结论：

定理2  当

时，系统(1)在R₀=1处存在后向分支.

定理3  当R₀ < 1时，系统(1)的无烟平衡点E₀是局部渐近稳定的；当R₀>1时，E₀不稳定.

证  系统(1)在E₀处的Jacobian矩阵为

特征方程为

(6)式有两个负的特征根λ₁=-μ，λ₂=-μ-δ，其余两个特征根满足下面方程

其中

且a₁>0，我们得出：

(ⅰ) 当R₀ < 1时，a₀>0，则λ₃λ₄>0，λ₃+λ₄ < 0，所以λ₃，λ₄均小于0，所以方程(6)的所有根都具有负实部，因此无烟平衡点E₀是局部渐近稳定的.

(ⅱ) 当R₀>1时，a₀ < 0，则λ₃λ₄ < 0，所以λ₃，λ₄的值是一正一负的，因此E₀是不稳定的.

定理4  当

时，无烟平衡点E₀是全局渐近稳定的.

证  这里容易验证R₁>R₀.

构造一个Lyapunov函数

其中$S_{0}=\frac{A}{\mu}$，L(t)≥0.

计算L(t)沿系统(1)解的全导数，则有

由于$2-\frac{S}{S_{0}}-\frac{S_{0}}{S} \leqslant 0$，故R₁≤1时，L′(t)≤0，且L^′(t)=0当且仅当$S=\frac{A}{\mu}$，I₁=0，I₂=0，R=0.那么，集合{(S，I₁，I₂，R)：L′(t)=0}的最大不变集为单点集{E₀}.根据定理3和Lyapunov-Lasalle原理^[12]，t→∞时，系统(1)所有的非负解均趋于无烟平衡点E₀，所以当R₁≤1时，E₀是全局渐近稳定的.

定理5  对于模型(1)，R₀>1时，系统是一致持续的，即存在一个正数ε，使得

证  定义

为了证明疾病的一致持续性，在∂X₀中，说明模型(1)的解与∂X₀的交集是空集.

首先，容易看出X是正不变集，X₀是正不变的，且∂X₀是X的相对闭集.令P：X→X是系统(1)的Pioncaré映射，即P(x⁰)=Φ(t，x⁰)，x⁰∈X，其中Φ(t，x⁰)是系统(1)满足初值条件Φ(0，x⁰)=x⁰的唯一解.记

下面证明M_∂={(S，0，0，R)：S≥0，R≥0}.即证明对所有t≥0，有I₁(t)=0和I₂(t)=0.假设该结论不成立，即可分以下两种情况讨论.

第一种情况：存在t₀≥0使得I₁(t)>0，I₂(t)=0，即有

由此可见，存在δ>0，当t₀≤t≤t₀+δ时$\frac{\mathrm{d} I_{2}}{\mathrm{~d} t}>0$.这说明t₀≤t≤t₀+δ时，(S(t)，I₁(t)，I₂(t)，R(t))∉M_∂，推出矛盾.

第二种情况：存在t₀≥0使得I₁(t)=0，I₂(t)>0，即有

由此可见，存在δ>0，当t₀≤t≤t₀+δ时$\frac{\mathrm{d} I_{1}}{\mathrm{~d} t}>0$. 这说明t₀≤t≤t₀+δ时，(S(t)，I₁(t)，I₂(t)，R(t))∉M_∂，推出矛盾.这就证明了M_∂={(S，0，0，R)：S≥0，R≥0}.

已知E₀=$\left(\frac{A}{\mu}, 0, 0, 0\right)$是P在M_∂上的一个不动点.如果(S(t)，I₁(t)，I₂(t)，R(t))是系统(1)在M_∂上的一个解，则$\lim\limits_{t \rightarrow \infty} S(t)=\frac{A}{\mu}$，$\lim\limits_{t \rightarrow \infty} I_{1}(t)=0$，$\lim\limits_{t \rightarrow \infty} I_{2}(t)=0$，$\lim\limits_{t \rightarrow \infty} R(t)=0$.若E₀是孤立的，则{E₀}是一个非循环覆盖.下面证明E₀是孤立的.首先证明W^s(E₀)∩X₀=φ成立.由解对初值的连续依赖性，∀η>0，∃ε>0，使得

有

下证$\limsup\limits_{m \rightarrow \infty}d\left(P^{m}\left(\boldsymbol{x}_{0}\right), \boldsymbol{E}_{0}\right) \geqslant \varepsilon$.假设不成立，则∃x₀∈X₀，使得$\limsup\limits_{m \rightarrow \infty}d$(P^m(x₀)，E₀) < ε，则||Φ(t，P^m(x₀))-Φ(t，E₀)|| < η，∀m≥0，∀t∈[0，c]，设t=mc+t₁，其中t₁∈[0，c]，m=$\left[\frac{t}{c}\right]$，则有

令(S(t)，I₁(t)，I₂(t)，R(t))=Φ(t，x₀)，t≥0，则

由系统(1)可以得到

考虑一个辅助系统

因为R₀>1，由文献[13]中的引理2.1和比较定理可得：

这与0≤I₁(t)≤η，0≤I₂(t)≤η矛盾，则W^s(E₀)∩X₀=φ，即M_∂中的每一个轨道都收敛于E₀，则E₀在M_∂中是非循环的.由一致持续的非循环定理知，P关于(X₀，∂X₀)是一致持续的.由文献[14]可知，系统(1)关于(X₀，∂X₀)是一致持续的.

本文基于吸烟传播的特点，考虑个体传播和媒介宣传传播这两个重要风险因素，建立了一个吸烟传播动力学模型.本文首先定义吸烟传播阈值，分析模型的平衡态，发现R₀ < 1时，模型可能有两个平衡态，其中一个是局部稳定的，这意味着模型出现后向分支，吸烟可能持续存在；R₀>1时，模型有唯一平衡点且模型一致持续，这说明在这种情况下，吸烟一定一直持续存在.最后，本文证明了无烟平衡态的局部渐近稳定性，说明了控烟到低水平的意义.研究结果丰富了吸烟传播动力学，拓展了人们对吸烟传播影响因素的认识，有利于吸烟控制措施的制定.