On Biweighted Composite Regression Estimation of GARCH Model

记y_t表示某资产第t天的收益率，则标准GARCH(p，q)模型为

其中：扰动序列{η_t，t≥1}为独立同分布的随机变量序列；v_t为y_t的条件标准差，v_t=Var(y_t|${\mathscr{F}}$_t)；${\mathscr{F}}$_t表示由{y_s；s≤t}生成的σ-域. 记参数α=(α₁，…，α_q)^T，β=(β₁，…，β_p)^T，γ=(α^T，β^T)^T且γ≥0，对应的真值分别为α^*=(α₁^*，…，α_q^*)^T，β^*=(β₁^*，…，β_p^*)^T，γ^*= (α^*T，β^*T)^T.

对应GARCH(p，q)模型的条件τ_k分位数为

其中ξ_k^*为扰动序列{η_t，t≥1}的第τ_k个真实分位数，也即满足P(η_t ≤ξ_k^*)=τ_k.

GARCH模型的CQR估计^[11]为

其中：分位数水平τ_k= $\frac{k}{1+K}$，k=1，…，K；条件分位数q_t(θ_k)=v_t(γ)ξ_k由式(1)可得；τ_k水平下损失函数定义为ρ_τk(u)=u(τ_k-I)(u < 0)，其中I为示性函数；参数空间Θ_μ的定义见假设1. 记参数ξ=(ξ₁，…，ξ_K)^T，θ_k=(ξ_k，γ^T)^T，θ=(ξ^T，γ^T)^T，对应的真值分别为ξ^*=(ξ₁^*，…，ξ_K^*)^T，θ_k^*=(ξ_k^*，γ^*T)^T，θ^*=(ξ^*T，γ^*T)^T.

注意到，当p，q≥0时，本文初值取为y₀=…=y_1-q=y₁，$\hat v$₀²=…=$\hat v$_1-p²=y₁²，取定初值后的v_t²(γ)对应为$\hat v$_t²(γ)=$1+\sum_{i=1}^{q} \alpha_{i} y_{t-i}^{2}+\sum_{j=1}^{p} \beta_{j} \hat{v}_{t-j}^{2}(\boldsymbol{\gamma})$.

将文献[12]提出的WCQR扩展至GARCH模型

其中：$\hat q$_t(θ_k)为给定初值下的条件分位数$\hat q$_t(θ_k)=$\hat v$_t(γ)ξ_k；ω_k表示τ_k分位数水平下损失函数对应的权重，对任意1≤k≤K有ω_k> 0，且$\sum_{k=1}^{K}ω_k=1$. 关于权重ω_k的选取详见注2.

将文献[14]提出的混合QR加权思想扩展到CQR，由此衍生出估计

其中$\hat v$_t为给定初值下CQR估计的条件标准差，$\hat v$_t=$\hat v$_t($\tilde γ$_n)，$\tilde γ$_n由式(2)计算可得.

将式(3)和式(4)相整合，即可得到本文提出的BWCQR估计

在给出BWCQR估计的渐进性质之前，须引入一些记号和模型假设：记向量a的欧几里得范数为‖a‖；C表示在不同的计算过程中不尽相同的任一正数；定义矩阵A=(a_ij)的欧几里得范数为‖A‖ =$\sum_{i，j}$ |a_ij|；V表示一广义可积随机变量；{S_t}表示一平方可积非负平稳遍历过程且满足S_t∈ ${\mathscr{F}}$ _t-1；变量ρ满足0 < ρ < 1；ρ_τk(u)关于u的导数为ψ_τk(u)=τ_k-I(u <0).

假设1    模型的真值θ^*为Θ_μ的内点，其中参数空间Θ_μ定义为

其中实数μ∈(0，1)且使得θ^*∈Θ_μ.

假设2    令多项式A(x)=$\sum_{i=1}^{q}$α_i^* xⁱ，B(x)=1-$\sum_{j=1}^{p}$ β_j^*x^j，对p，q>0有α_q^*＞0，β_p^*≠0. 多项式A(x)和B(x)没有公因子.

假设3   (i) 扰动η_t满足E(η_t²) < ∞；(ii) 记η_t的累积分布函数为F，对应的密度函数为f. f可积且对1≤k≤K满足f(F^-1(τ_k))>0，且有sup_x|f(x)|≤C₁，sup_x|f′(x)|≤C₂，其中实数C₁，C₂>0，f在ξ_k^*的邻域内连续.

假设4   矩阵$E\left(\frac{\partial q_{t}\left(\boldsymbol{\theta}_{k}^{*}\right)}{\partial \boldsymbol{\theta}} \frac{\partial q_{t}\left(\boldsymbol{\theta}_{k}^{*}\right)}{\partial \boldsymbol{\theta}^{\mathrm{T}}}\right)$为正定矩阵.

定理1    在假设1-3满足的条件下，有n→∞时$\hat{\boldsymbol{\theta}}_{n} \stackrel{p}{\longrightarrow} \boldsymbol{\theta}^{*}$.

为了简便，记v_t=v_t(γ^*)，$\tilde v$_t=v_t($\tilde {{\mathit{\pmb{γ}}}}_n$)，$\hat v$_t= $\hat v$_t($\tilde {\mathit{\pmb{γ}}}_n$)，其中$\tilde {\mathit{\pmb{γ}}}_n$表示复合分位数的参数估计(CQRE)；q_t(θ_k)=ξ_kv_t(γ)和$\hat q$_t(θ_k)=ξ_k$\hat v$_t(γ)分别表示未给定初值和给定初值τ_k水平下的条件分位数. 文献[10]的推论A.1-A.7给出了q_t(θ_k)，$\hat q$_t(θ_k)，v_t(γ)和$\hat v$_t(γ)及其导数的相关性质，本文中简记为A.1-A.7.

证明  分别定义

其中l_k(θ)=ρ_τk(y_t-q_t(θ_k))，$\hat l$_k(θ)=ρ_τk(y_t-$\hat q$_t(θ_k))，q_t(θ_k)=ξ_kv_t(γ)，$\hat q$_t(θ_k)=ξ_k$\hat v$_t(γ). 为了方便，定义d_t(θ_k)=q_t(θ_k)-q_t(θ_k^*)，$\hat d$_t(θ_k)=$\hat q$_t(θ_k)-$\hat q$_t(θ_k^*)，η_tk=η_t -ξ_k^*.

本文主要证明定理2及推论3，定理1不作详细证明. 关于定理1可参考文献[15]中定理1的证明，分证四点即可：

1) $\sup\limits _{\boldsymbol{\theta} \in \Theta_{\mu}}\left|\hat{S}_{n}(\boldsymbol{\theta})-S_{n}(\boldsymbol{\theta})\right|=o_{p}(1)$；

2) $\sum_{k=1}^{K} \omega_{k} E\left(\sup\limits _{\boldsymbol{\theta} \in \Theta_{\mu}} v_{t}^{-1} l_{k}(\boldsymbol{\theta})\right)<\infty$；

3) $\sum_{k=1}^{K} \omega_{k} E\left(v_{t}^{-1} l_{k}(\boldsymbol{\theta})\right)$在θ^*处有唯一最小值；

4) 对任一θ^#∈Θ_μ，当$\ell$→0时有$\sum_{k=1}^{K} \omega_{k} E\left(\sup\limits _{\boldsymbol{\theta} \in B_{\ell}(\boldsymbol{\theta} ^{\#})} v_{t}^{-1}\left[l_{k}(\boldsymbol{\theta})-l_{k}\left(\boldsymbol{\theta}^{\#}\right)\right]\right)$→0，其中B_$\ell$(θ^#)={ θ^#∈Θ_μ：|θ^#-θ| < $\ell$}表示以θ^#为中心$\ell$为半径的邻域.

定理2   在假设1-4满足的条件下，有$\sqrt{n}\left(\hat{\boldsymbol{\theta}}_{n}-\boldsymbol{\theta}^{*}\right) \stackrel{d}{\longrightarrow} N\left(\bf{0}, \boldsymbol{D}^{-1} \boldsymbol{C D}^{-1}\right)$，其中矩阵C，D分别为：

注1    当K=1，ω= 1 且v_t=1时，定理2退化为QR估计的渐进性质，详见文献[10]定理2；当K=1且ω= 1 时，定理2退化为混合QR的渐进性质，详见文献[15]定理2；当ω= 1 且v_t=1时，定理2退化为CQR的渐进性质，详见文献[11]定理2.

引理1   在假设1-3满足的条件下，定义δ= $\sqrt n$(θ-θ^*)，有

其中G_n(θ)=S_n(θ)-S_n(θ^*)，$\tilde G$_n(θ)= $\tilde S$_n(θ)- $\tilde S$_n(θ^*)，$\hat G$_n(θ)=$\hat S$_n(θ)-$\hat S$_n(θ^*).

证明

可分别证$\tilde R$_1n(θ)=o_p(|δ|)与$\tilde R$_2n(θ)=o_p(|δ|²).

1) 分别对d_t(θ_k)及$\hat d$_t(θ_k)进行泰勒展开

注意到，对∀τ∈(0，1)有ρ_τ(x)≤|x|. 由ρ_τ(x)的Lipschitz连续性及式(6)，有

其中θ′为介于θ^*与$\boldsymbol{\theta}^{*}+\frac{\boldsymbol{\delta}}{\sqrt{n}}$之间的p+q+K维向量，θ′_k为θ′的p+q+1维子向量(ξ′_k，γ^′T)^T. 由A.4及|v_t²|≥1不难得到

因此，由式(8)及A.2有

2) 定义

由文献[16]有等式

定义η_tk=η_t-ξ_k^*，对∀c>0，ψ_τ(x)=ψ_τ(cx)且由式(9)可以得到等式

将式(10)和式(11)代入$\tilde R$_2n(θ)有$\tilde R$_2n(θ)$\triangleq \widetilde{\Pi}_{1}$(δ)+$\widetilde{\Pi}_{2}$(δ)+$\widetilde{\Pi}_{3}$(δ)+$\widetilde{\Pi}_{4}$(δ)，其中

将式(6)代入$\widetilde{\Pi}_{1}$(δ)，由A.4及|ψ_τ(x)| < 1有

据ψ_τ(x)的定义对其应用Fubini定理及泰勒展开有

其中ξ_k1介于ξ_k^*和ξ_k^*$\tilde v$_tv_t^-1之间. 故由假设3、重期望、A.2与A.7及式(6)可得

注意到| $\tilde B$_tk|≤2，由此同对$\widetilde{\Pi}_{1}$(δ)的讨论类似，可以得到$\widetilde{\Pi}_{3}$(δ)=o_p(|δ|).

最后考虑$\widetilde{\Pi}_{4}$(δ). 由Fubini定理及泰勒展开有

其中ξ_k2=ξ_k^*$\hat v$_t(γ^*)v_t^-1+v_t^-1$\hat d$_t(θ_k)s₂和ξ_k3=ξ_k^*+v_t^-1d_t(θ_k)s₃，0 < s₂，s₃ < s≤1. 故由假设3、式(6)及A.2与A.4可得

引理2   在假设1-3满足的条件下，有

证明   引理2的证明同引理1的证明类似

据文献[17]定理3.1和式(9)易证K_1n(δ)=o_p(|δ|)与K_2n(δ)=o_p(|δ|²).

引理3   在假设1-3满足的条件下，有

其中

证明   由式(9)有

对R_1n(δ)泰勒展开：R_1n(δ)=-δ^TC_n-δ^TK_3n(θ′)δ，其中

其中θ′为介于θ^*与θ^*+ $\frac{\boldsymbol{\delta}}{\sqrt{n}}$之间的p+q+K维向量，θ′_k为θ′的p+q+1维子向量(ξ′_k，γ^′T)^T. 由文献[10]A.2及S_t为二阶可积广义平稳遍历过程可得Var(K_3n(θ′))→0，因此K_3n(θ′)=o_p(1)，也即R_1n(δ)=-δ^TC_n+o_p(|δ |²).

定义B_tk=B_tk1+B_tk2，其中

对R_2n(δ)泰勒展开有R_2n(δ)$\triangleq$K_4n(δ)+K_5n(δ)+K_6n(δ)+K_7n(δ)，其中

对E(B_tk1|${\mathscr{F}}$_t-1)应用Fubini定理及泰勒展开，则K_4n(δ)= $\frac{1}{2}$δ^TD_nδ+δ^T${{{{\mathbf{\Pi}}}}}$_1n(δ)δ，其中0 < s′ < s≤1，

由中值定理、文献[10]A.2及假设3，对∀ζ>0

当ζ→0时，式(14)趋于0. 也即对∀ε，λ>0，存在ζ₀=ζ₀(ε)>0使得对∀n≥1有P($ \begin{array}{c} \sup\limits_{\mid \boldsymbol{\theta}-\boldsymbol{\theta}^{*} \mid \leqslant \zeta_{0}} \end{array}$‖Π_1n(δ)‖>λ) < $\frac {ε}{2}$. 当n足够大时，θ-θ^*=o_p(1)，因此P(|θ-θ^*|>ζ₀) < $\frac {ε}{2}$. 当n足够大时

故K_4n(δ)= $\frac {1}{2}$δ^TD_nδ+o_p(|δ|²).

对K_5n(δ)进行放缩后

应用文献[15]引理3可得K_5n(δ)=o_p(|δ|+|δ |²). 由文献[10]A.2及|B_tk2|≤2、|B_tk|≤2可分别得到K_6n(δ)=o_p(|δ|)，K_7n(δ)=o_p(|δ|²)，由此R_2n(δ)=$\frac {1}{2}$δ^TD_nδ+o_p(|δ|+|δ |²).

定理2证明   结合引理1-3和定理1，同文献[15]中定理2的证明类似即可证明该定理.

推论1   在假设1-4满足的条件下，有$\sqrt{n}\left(\hat{\boldsymbol{\gamma}}_{n}-\boldsymbol{\gamma}^{*}\right) \stackrel{d}{\longrightarrow} N(\bf{0}, \boldsymbol{U})$，其中U为D^-1CD^-1的右下角(p+q)×(p+q)维矩阵：

其中Σ=$\operatorname{Var}\left(\frac{1}{v_{t}} \frac{\partial v_{t}}{\partial {\boldsymbol{\gamma}}}\right)$.

注2   令

据推论1可知Σ与权重ω无关，因此在$\sum_{k-1}^{K} \omega_{k}=1$及ω> 0 的条件下，通过极小化σ²(ω)即可得到权重向量ω的数值解.

推论1证明  矩阵C可分为4块分块矩阵

其中：C₁₁为K×K维矩阵，其(i，j)元素为ω_iω_j(τ_i∧τ_j-τ_iτ_j)；C₁₂为K×(p+q)维矩阵，其第i行向量为$\sum_{j=1}^{K}$ω_iω_j(τ_i∧τ_j-τ_iτ_j)ξ_j^*$E\left(\frac{1}{v_{t}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}^{\mathrm{T}}}\right)$且C₂₁=C₁₂^T；C₂₂为(p+q)× (p+q)维矩阵，C₂₂=$\sum_{i=1}^{K}\sum_{j=1}^{K}$ω_iω_j(τ_i∧τ_j-τ_iτ_j)ξ_i^*ξ_j^*$E\left(\frac{1}{v_{t}^{2}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}^{\mathrm{T}}}\right)$.

同样可以将矩阵D分为4块分块矩阵

其中：D₁₁为K× K维对角矩阵，其第i个元素为ω_if(ξ_i^*)；D₁₂为K×(p+q)维矩阵，其第i行向量为ω_if(ξ_i^*)ξ_i^*$E\left(\frac{1}{v_{t}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}^{\mathrm{T}}}\right)$且D₂₁=D₁₂^T；D₂₂为(p+q)×(p+q)维矩阵D₂₂=$\sum\limits_{k=1}^{K} \omega_{k} f\left(\xi_{k}^{*}\right) \xi_{k}^{* 2} E\left(\frac{1}{v_{t}^{2}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}} \frac{\partial v_{t}}{\partial \boldsymbol{\gamma}^{T}}\right)$.

注意到，在假设4及权重向量ω> 0 的条件下矩阵D，C均为严格正的可逆矩阵，矩阵D^-1 CD^-1的右下块(p+q)× (p+q)维矩阵U为

其中

经计算可得推论1成立.

将本文提出的BWCQR分为如下6个步骤：

(i) 运用式(2)计算出CQR估计$\widetilde{\boldsymbol{\theta}}_{n}=\left(\widetilde{\boldsymbol{\xi}}_{n}^{\mathrm{T}}, \widetilde{\boldsymbol{\gamma}}_{n}^{\mathrm{T}}\right)^{\mathrm{T}}$；

(ii) 据步骤(i)可计算出条件标准差序列$\hat v$_t=$\hat v$_t($\tilde γ$_n)，进而计算出扰动序列$\hat \eta_{t}=\frac{y_{t}}{\hat {v}_{t}\left(\tilde \gamma_{n}\right)}$；

(iii) 对步骤(ii)中的$\hat \eta$_t采用核光滑估计可以得到其密度函数f(·)的估计；

(iv) 计算步骤(ii)中的$\hat \eta$_t的τ_k经验分位数$\tilde ξ$_k^*；

(v) 据步骤(iii)和(iv)即可确定权重目标函数σ²(ω)，由此可解得ω的非参数数值解$\tilde {\boldsymbol{ω}}$；

(vi) 将步骤(ii)中$\hat v$_t和步骤(v)中$\tilde {\boldsymbol{ω}}$代入式(3)、式(4)及式(5)，可得估计$\hat {\boldsymbol{θ}}$_n¹，$\hat {\boldsymbol{θ}}$_n²和$\hat {\boldsymbol{θ}}$_n.

基于GARCH(1，1)模型

利用蒙特卡洛数值模拟检验本文所提BWCQR方法在有限样本下相较QML，QR和CQR方法的稳健性和有效性. 数值模拟模型参数选取如下：

(i) 分别考虑扰动项序列η_t服从标准正态分布N(0，1)，t(5)分布和t(3)分布；

(ii) 样本容量分别取n=300，500，1 000和1 500进行300次重复抽样；

(iii) 复合分位数回归模型中K值取5，9和19，QR估计的风险水平取0.3，0.5和0.7；

(iv) 本文采用估计量的偏差(Bias)、标准差(SD)和均方误差(MSE)作为估计的评价标准.

为了方便起见，分别将K时的$\tilde {{\mathit{\pmb{θ}}}}$_n，$\hat {{\mathit{\pmb{θ}}}}$_n¹，$\hat {{\mathit{\pmb{θ}}}}$_n²和$\hat {{\mathit{\pmb{θ}}}}$_n的估计方法记为CQR_K，WCQR_K¹，WCQR_K²和BWCQR_K. 表 1-3给出了3种分布下的数值模拟结果.

分析结果得到：

(i) 无论扰动序列的分布如何，对任一估计，随着样本量n的增大，MSE愈小；

(ii) 各类复合分位数估计对K值的敏感程度不强；

(iii) 样本规模n一定时，K越大，MSE越小，也即K取19时各类复合分位数回归估计最优；

(iv) 当扰动项服从正态分布时，QMLE最优；

(v) 当扰动项服从重尾分布时，总体而言，BWCQR估计明显优于WCQR¹，略优于WCQR²，且随着K的增加BWCQR估计的竞争力愈强.

选取上证和沪深300股指作为研究对象，实证区间为2015年1月5日至2021年5月11日，共计1 544个样本数据. 记p_t为第t交易日的收盘价，r_t为百倍对数收益率：r_t=100×(lnp_t-lnp_t-1).

表 4给出r_t序列的描述性统计分析值. 均值大于0，说明股指整体趋势上行，且序列不服从正态分布、不独立同分布. 综上所述，足以表明r_t序列具有典型的高峰厚尾特征. Ljung-Box检验Q统计量和ADF检验表明序列具有明显的长记忆性且平稳.

本文选用GARCH(1，1)对该时间序列进行建模分析，采用向前一步滚动窗口预测方法，并将2015年1月5日至2020年1月23日作为初始滚动窗口. 本文对r_t分别采用QMLE，MLE-t和BWCQR₁₉进行拟合，对应标准化残差序列的ARCH-LM检验通过率列于表 5. 表 5结果符合数值模拟结论，BWCQR估计明显优于QMLE和MLE-t.

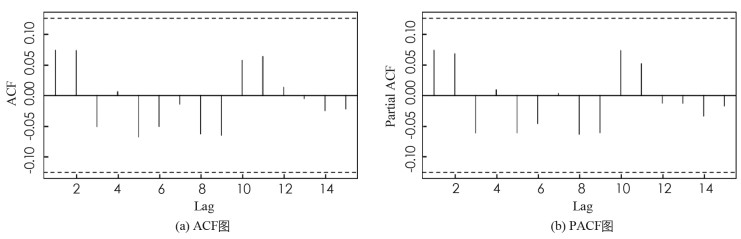
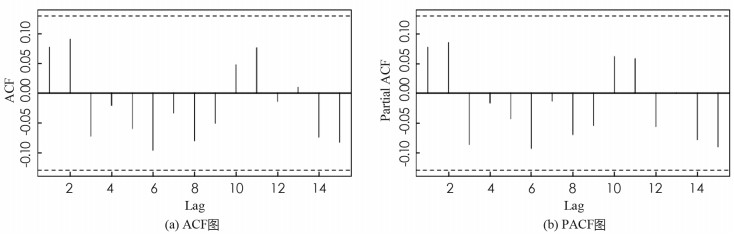
进一步，上证指数全序列和沪深300股指全序列在BWCQR估计下的标准化残差序列的自相关(ACF)图和偏自相关(PACF)图，如图 1，2所示，可见BWCQR估计下股指的标准化残差序列是白噪声序列，这再次验证了BWCQR估计的优良性.

本文提出了GARCH模型的BWCQR估计并探究其大样本性质. 数值模拟结果显示：当扰动项序列服从正态分布时，QML估计略优于BWCQR估计；当扰动项序列服从厚尾分布时，BWCQR估计明显优于传统估计. 我们将提出的BWCQR拟合分析上证和沪深股指波动系统，结果表明BWCQR估计能更为合理有效地刻画股指时序的波动规律.