-
结核病是一种慢性传染病,主要由结核分枝杆菌感染引起[1]. 关于结核病的传播机制和动态,已经有了许多研究成果[2-7]. 其中,文献[6]考虑结核病的外源性传染因素,建立了动力学模型. 但该模型将人口输入设定为常数,与实际情况不吻合. 本文在已有研究的基础上,建立如下模型:
其中:S(t),E(t),I(t)分别表示易感者、潜伏者、染病者的数量;m为环境容纳量;r为内禀增长率;β为易感人群与感染者的接触率;k为潜伏者向染病者的转移率;μ为自然死亡率;μd为因病死亡率;p为潜伏者遇到染病者的加速感染率. 所有参数均为正.
本文结构如下:第一节求模型(1)的基本再生数,并分析模型平衡点的存在性;第二节主要研究模型的Hopf分支和尖点分支;第三节用数值模拟验证分析结果;第四节进行总结.
HTML
-
根据文献[8]的方法,模型(1)有正不变集
其中:
$\eta, M=\frac{(r+\eta)^2 m}{4 r}$ 都为正.模型的无病平衡点为$\boldsymbol{P}_0=\left(S^0, 0, 0\right)=(m, 0, 0)$ ,根据下一代矩阵法[9],模型的基本再生数为正平衡点
$\boldsymbol{P}_*=\left(S^*, E^*, I^*\right)$ 满足:可得
$S^*=\frac{\left(\mu+\mu_d\right)\left(p \beta I^*+\mu+k\right)}{\beta\left(p \beta I^*+k\right)}, E^*=\frac{\left(\mu+\mu_d\right) I^*}{p \beta I^*+k} .$ 且I*满足
其中
由于D(I*)=0时I*的解小于零,所以只需考虑f(I*)=0的情况.因此,有以下定理:
定理1 当R0>1时,C < 0,模型(1)有一个正平衡点;当R0 < 1时,C>0,如果B < 0,模型(1)有两个正平衡点;当R0=1时,C=0,如果B < 0,模型(1)有一个正平衡点.
-
当R0 < 1时,无病平衡点P0是局部渐近稳定的;当R0>1时,无病平衡点P0是不稳定的.根据Sotomayor’s定理[10],当R0=1且pμr≠μk+k2时,模型(1)发生跨临界分支.由于R0 < 1时,模型(1)可能有两个正平衡点,根据文献[6]的方法,当R0=1且pμr>μk+k2时,模型经历后向分支.接下来讨论模型的Hopf分支和尖点分支.
-
对模型(1)作变换
$(x, y, z)=\left(S-S^*, E-E^*, I-I^*\right)$ ,在原点泰勒展开,我们得到其中
此时,正平衡点P*的特征方程为
其中
当p=p1时,我们有α1(p1)>0和α2(p1)α1(p1)-α0(p1)=0,那么特征方程变为
有一个负根λ1=-α2(p1)和一对纯虚根
$(\lambda_{2, 3}=\pm \mathrm{i} \sqrt{\alpha_1\left(p_1\right)}$ . 对于足够小的ε>0,当p∈(p1-ε,p1+ε)时,特征值的形式如下将λ2带入特征方程(8)中,对p求导,分离实部和虚部,得到
其中
则有
当p穿过临界值p1时,Hopf分支发生.
通过变换
我们得到
其中
$M_{m n s}, N_{m n s} \text { 和 } L_{m n s}$ 是依赖于p,β,r,μ,μd和k的系数.P*的局部中心流形有以下形式其中
模型限制在中心流形
上,其中
Lyapunov第一系数可以表示为
基于上述分析,我们有以下定理:
定理2 对于模型(1),如果l1 < 0(>0),那么Hopf分支是超临界的(亚临界的),如果l1=0,那么Hopf分支是退化的.
-
对于正平衡点
$\boldsymbol{P}_*=\left(S^*, E^*, I^*\right)$ 的特征方程(8)式,如果α1=0且α0=0,则特征值为λ1,2=0,λ3=-α2,模型(1)可能发生一个余维2的B-T分支.特征值λ1,2=0对应的特征向量和广义特征向量为U1=$\left(\frac{c h}{a}, j, -h\right)^{\mathrm{T}} \text { 和 } \boldsymbol{U}_2=\left(\frac{c h}{a^2}, -1, 0\right)^{\mathrm{T}}, \lambda_3=-\alpha_2$ 对应的特征向量为$\boldsymbol{U}_3=\left(\frac{c h}{e+j}, a+e, h\right)^{\mathrm{T}} \text {. 令 }(x, y, z)=$ $\left(S-S^*, E-E^*, I-I^*\right)$ ,将模型(1)在原点泰勒展开成(7)式,通过变换其中
$\boldsymbol{G}=\left(\boldsymbol{U}_1, \boldsymbol{U}_2, \boldsymbol{U}_3\right)$ ,模型变为其中
根据文献[11]的方法,模型(14)存在一个中心流形,可以局部表示为
ε1和ε2足够小.考虑中心流形
将中心流形带入模型(14)的第三式,得到
限制在中心流形上的模型为
通过变换
得到
则有以下定理成立:
定理3 令
$R_0=1, \alpha_1=0, B_{20} \neq 0 \text { 且 } B_{11}+2 A_{20} \neq 0 \text {. }$ 则正平衡点P*是一个余维2的尖点.
2.1. Hopf分支
2.2. 尖点分支
-
本节通过数值模拟,分析模型(1)的动力学性态.固定参数
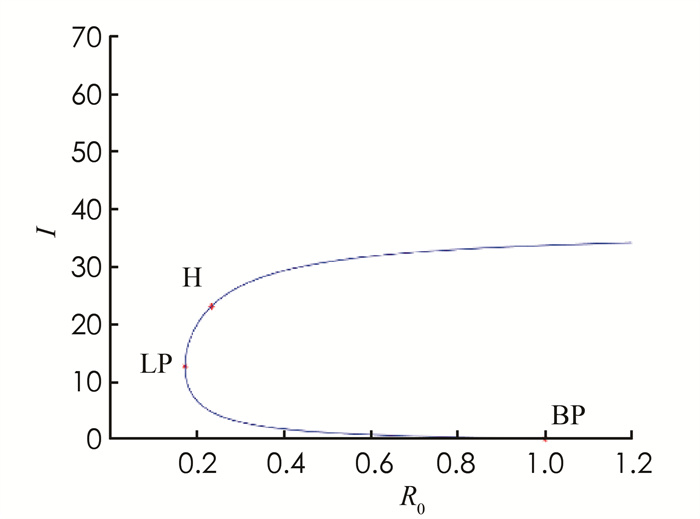
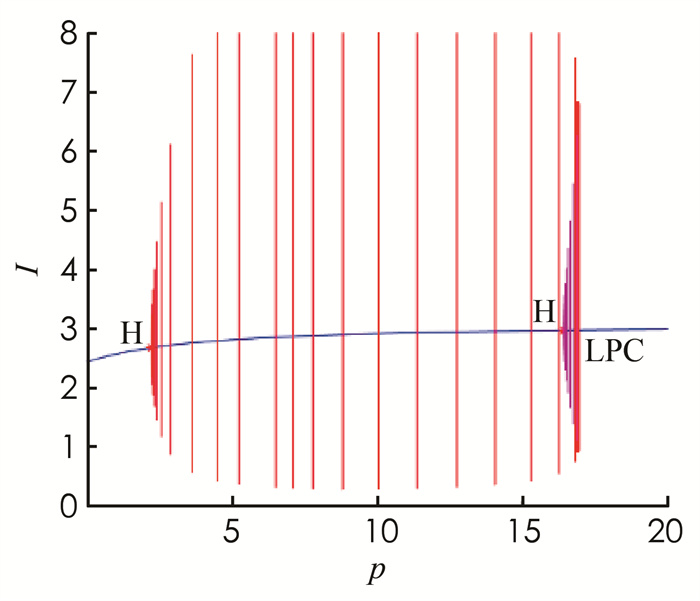
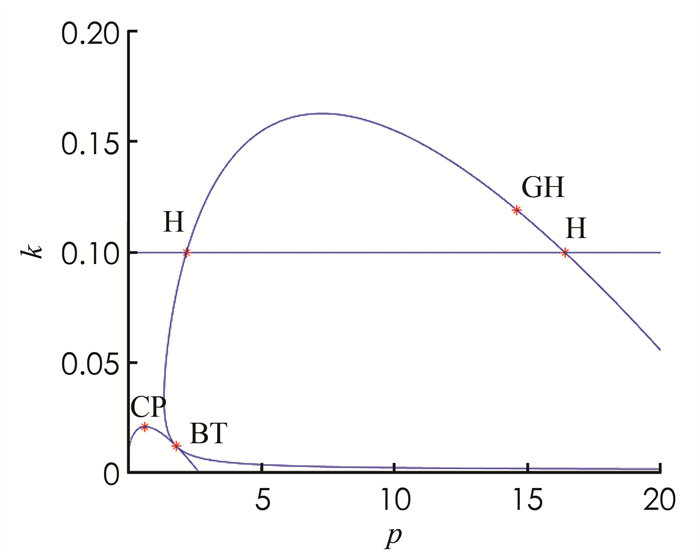
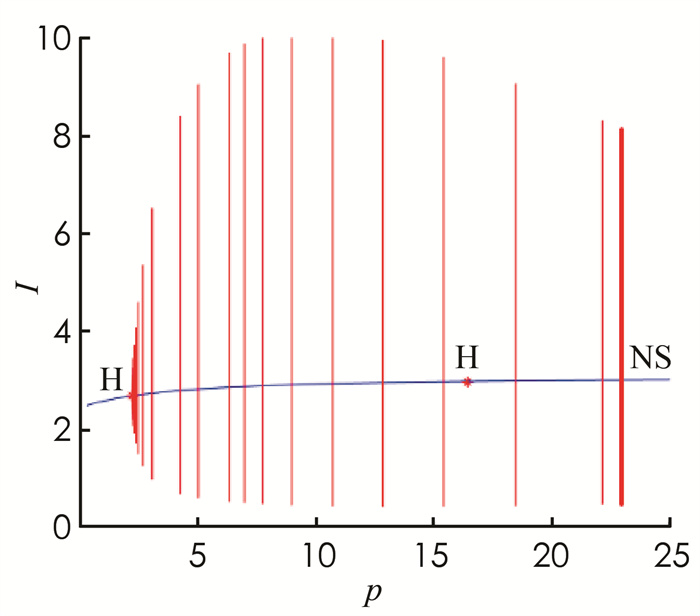
$r=4, m=70, p=0.5, \mu=0.95, k=0.05$ ,模型随着d的变化发生后向分支,R0 < 1时出现了一个Hopf点(图 1).再选择p作为分支参数,固定参数$r=0.04, m=35, \beta=0.01, \mu=0.07, \mu_d=0.01, k=0.1$ ,模型随着参数p的变化出现两个Hopf点,从第一个Hopf点出发到第二个Hopf点右侧出现一个稳定的极限环,然后变得不稳定,最后在第二个Hopf点消失(图 2).选择p和k作为分支参数,随着参数p和k的变化模型会出现B-T分支点,CP分支点和退化的Hopf分支点GH(图 3).随着参数p和r的变化,模型在第二个Hopf分支点右侧出现中性鞍点(图 4).
-
本文基于结核病传播的特点,考虑logistic出生和外源性再感染,建立一个反映结核病传播特点的动力学模型.利用稳定性分析方法,首先确定了模型的基本再生数,分析了正平衡点的存在性;然后利用规范型理论研究发现,模型(1)不仅出现余维1的跨临界、后向和Hopf分支,还会出现余维2的尖点和Hopf分支(退化的Hopf分支);最后通过数值模拟验证理论结果,分析给出周期解出现与消失的情况,并发现模型会出现B-T分支.这些复杂的动力学性态说明:当基本再生数R0 < 1时,外源性感染也可能导致地方病存在;周期解的存在意味着即使疾病处在低水平也不能说明疾病会逐渐消亡,这给疾病防控措施的制定带来很多困难.






 DownLoad:
DownLoad: