Hopf Bifurcation Analysis in the Diffusive Nutrient-Microorganism Model with Time Delay

本节考虑如下带有时滞参数的常微分系统：

易知系统(5)存在正常数平衡点(u^*，v^*)的充要条件为(u^*)²+(1－b)u^*+K=0，因此可知：

若$b<1+2 \sqrt{K}$，则系统(5)不存在正常数平衡点；

若$b=1+2 \sqrt{K}$，则系统(5)存在1个正常数平衡点$\left(u_0^*, v_0^*\right)=(\sqrt{K}, 1+\sqrt{K})$；

若$b>1+2 \sqrt{K}$，则系统(5)存在2个正常数平衡点(u₁^*，v₁^*)和(u₂^*，v₂^*)，其中

根据文献[2]可知，当τ=0，且系统(5)满足条件

时，正常数平衡点(u₁^*，v₁^*)是局部渐近稳定的，下面讨论时滞τ≠0对系统(5)的正常数平衡点(u₁^*，v₁^*)稳定性的影响. 定义(u^*，v^*)=(u₁^*，v₁^*).

令$\hat{u}=u-u^*, \hat{v}=v-v^*$，为了方便起见，系统(5)可化为

其中

根据Taylor展开式，系统(6)在(0，0)处的线性化系统是

系统(7)的特征方程为

其中

若λ=iω(ω>0)是特征方程(8)的纯虚根，将其代入，可得

则有

其中

假设C₀²－B² < 0成立，则方程(10)存在正根ω₀，满足

将ω₀代入(9)式，计算可得

下面验证横截条件. 令

对其积分后代入ω=ω₀，可得

因此，当ω=ω₀时横截条件成立，可得定理1：

定理1  设$b>1+2 \sqrt{K}, 0<a<\frac{\left(u^*\right)^2+u^*+K}{K}, C_0^2-B^2<0$，则有：

(ⅰ) 若τ < τ₀⁰，则系统(5)的正常数平衡点(u^*，v^*)局部渐近稳定；

(ⅱ) 若τ=τ₀^j(j∈$\mathbb{N}$₊)，则系统(5)在正常数平衡点(u^*，v^*)处产生Hopf分支；

(ⅲ) 若τ>τ₀⁰，则系统(5)的正常数平衡点(u^*，v^*)不稳定.

本节研究如下带有时滞参数的偏微分系统，为了简化后期计算和着重探讨时滞因素对系统稳定性的影响，此时考虑空间域Ω=(0，lπ)的一维简单情形，其中l∈$\mathbb{R}$₊：

与1.1节类似，对系统(13)在平衡点(u^*，v^*)处做平移变换后，可以写成下面的抽象微分方程形式：

其中定义X=C([0，lπ]，$\mathbb{R}$²)，dΔ=(d₁Δ，d₂Δ)，以及

已知

对于ϕ=(ϕ₁，ϕ₂)^T∈C([－τ，0]，X)，有

以及

则系统(14)在(0，0)处附近的线性化系统为

线性系统(15)的特征方程等价于

根据特征值问题－ψ″=μψ，其中x∈(0，lπ)，ψ′(0)=ψ′(lπ)=0，可得特征值$\mu_n=\frac{n^2}{l^2}(n=0, 1, 2, \cdots)$以及对应的特征函数$\psi_n(x)=\cos \frac{n}{l} x$. 将$\boldsymbol{y}=\sum\limits_{n=0}^{\infty} \cos \frac{n}{l} x\left(\begin{array}{l} y_{1 n} \\ y_{2 n} \end{array}\right)$代入特征方程(16)，得到

因此，方程(16)的所有特征根由以下特征方程给出：

其中

若λ=±iω(ω>0)是特征方程(17)的一对纯虚根，则有

化简可得

其中

假设C₀²－B² < 0成立. 由于$\lim\limits_{n \rightarrow \infty}\left(C_n^2-B^2\right)=+\infty$，则存在最小的N₀≥0，使得：当n>N₀时，方程(19)没有正根；当0≤n≤N₀时，方程(19)至多有1个正根. 此外，假设d₂≥d₁，则A_n²－2C_n>0总是成立.

对于0≤n≤N₀，方程(19)有正根ω_n，满足

因此，可以确定τ的表达式为

其中

故此时方程(17)存在一对纯虚特征根±iω_n.

引理1  令λ_n(τ)=α_n(τ)+iω_n(τ)是方程(17)的根，当τ趋近于τ_n^j时，满足α_n(τ_n^j)=0和ω_n(τ_n^j)=ω_n，则有横截条件成立，即当0≤n≤N₀和j∈$\mathbb{N}$₊时，有$\left.\frac{\mathrm{d} \alpha_n}{\mathrm{~d} \tau}\right|_{\tau=\tau_n^j}>0$成立.

证  对特征方程(17)两边同时关于τ求导，则有

将τ=τ_n^j代入(25)式，可得

由于

以及

故由(26)式，有

因此横截条件成立. 证毕.

根据(23)式易得τ_n^j+1>τ_n^j. 接下来给出τ_n^j关于n的单调性.

引理2  若$d_2 \geqslant d_1, b>1+2 \sqrt{K}, 0<a<\frac{\left(u^*\right)^2+u^*+K}{K}$，则存在正整数M>0，使得当M≤n≤N₀，j∈$\mathbb{N}$₊时，有τ_n+1^j>τ_n^j成立.

证  由(22)式变形，可得

其中A_n²－2C_n和C_n²－B²由(20)，(21)式给出. 经计算可知，由于d₂≥d₁，所以A_n²－2C_n关于n是严格递增的，并且存在正整数M>0，使得当M≤n≤N₀时，B²－C_n²关于n是严格递减的，因此可得ω_n+1² < ω_n². 又因为

即有

故有A_n>0，再根据(24)式得$\tau_n^0=\frac{1}{\omega_n} \arccos \frac{\omega_n^2-C_n}{B}$，因此当M≤n≤N₀时，有τ_n+1⁰>τ_n⁰. 又因为ω_n+1 < ω_n，则由(23)式可知τ_n+1^j>τ_n^j，其中M≤n≤N₀，j∈$\mathbb{N}$₊. 证毕.

由引理2可知分支值序列{τ_n^j}中最小的分支值是τ₀⁰. 因此可以得到定理2：

定理2  设$d_2 \geqslant d_1, b>1+2 \sqrt{K}, 0<a<\frac{\left(u^*\right)^2+u^*+K}{K}$，则有：

(ⅰ) 若τ∈[0，τ₀⁰)，则系统(13)的正常数平衡点(u^*，v^*)局部渐近稳定；

(ⅱ) 若τ∈(τ₀⁰，∞)，则系统(13)的正常数平衡点(u^*，v^*)不稳定；

(ⅲ) 若τ=τ_n^j(0≤n≤N₀，j∈$\mathbb{N}$₊)，则系统(13)在正常数平衡点(u^*，v^*)处产生Hopf分支.

本节主要利用时滞偏微分方程的中心流形定理(见文献[14])和规范型理论(见文献[15-16])研究当τ=τ₀≡τ₀⁰时Hopf分支的方向和分支周期解的稳定性. 令τ=τ₀+μ，将$t=\tau \tilde{t}$代入方程(14)，且依旧用t表示$\tilde{t}$，则方程(14)改写为

其中对于ϕ∈C([－1，0]，X)，有

系统(14)在(0，0)处的线性化系统是

由第二节知，±iω₀τ₀是线性化系统(28)的一对纯虚特征值. 根据Riesz表示定理，存在一个2×2的有界变差函数矩阵η(θ，μ)(θ∈[－1，0])，满足以下形式：

其中

且对于δ(θ)：[－1，0] (X，X)，有

接下来定义算子A(0)和A^*分别为

其中ϕ(θ)∈C¹([－1，0]，$\mathbb{R}$²)，ψ(s)∈C¹([0, 1]，($\mathbb{R}$²)^*).

对于u=(u₁，u₂)，v=(v₁，v₂)∈X=C([0，lπ]，$\mathbb{R}$²)，定义内积为

此外，对于ϕ(θ)∈C¹([－1，0]，$\mathbb{R}$²)和ψ(s)∈C¹([0, 1]，($\mathbb{R}$²)^*)，引入如下双线性型内积：

经验证可知，±iω₀τ₀是算子A(0)和A^*的特征值，设q(θ)是算子A(0)关于特征值iω₀τ₀的特征向量，q^*(s)是算子A^*关于特征值－iω₀τ₀的特征向量，则根据算子A(0)和A^*的定义可得，q(θ)和q^*(s)的形式分别为

和

再根据(30)式，计算可得

由于q(θ)和q^*(s)满足〈q^* (s)，q(θ)〉₀=1和〈q^* (s)，q(θ)〉₀=0，则有

令系统(28)的中心子空间是Y={(zq(θ)+zq(θ))：z∈$\mathbb{C}$}. 在系统(27)中设μ=0，可确定一个中心流形为

设Φ=(q(θ)，q(θ))，Ψ=(q^*(s)，q^*(s))^T，且系统(27)在中心流形中的流可以写为

再根据内积公式可得〈ϕ，f₀〉=(〈ϕ，f₀¹〉，〈ϕ，f₀²〉)^T，其中ϕ∈C([－1，0]，X)，f₀=(f₀¹，f₀²)^T，f₀¹=$\left(\begin{array}{l} 1 \\ 0 \end{array}\right), \boldsymbol{f}_0^2=\left(\begin{array}{l} 0 \\ 1 \end{array}\right)$. 因此，当μ=0时，有

其中

根据G(ϕ，μ)的表达式可知G(ϕ，0)=τ₀F₀(ϕ)=τ₀(G₁，G₂)^T，其中

其中O(4)=O(‖(u，v)‖⁴).

由(32)-(34)式可得

为了得到g₂₁的值，需计算W₂₀(θ)和W₁₁(θ). 由于W(z(t)，z(t))满足

其中

I为单位矩阵，通过链式法则

可得

当θ∈[－1，0)时，由(35)式可得

则有

结合(36)和(37)式得到如下微分方程

可得方程(38)的解为

当θ=0时，由(36)式和

可得

其中

基于上述分析，可以计算出如下用于判断Hopf分支方向和分支周期解稳定性的值：

由此可得出定理3：

定理3  对于系统(13)，有如下结论：

(ⅰ) μ₂确定Hopf分支的方向，当μ₂>0(μ₂ < 0)时，分支方向是超临界的(次临界的)；

(ⅱ) β₂确定分支周期解的稳定性，当β₂ < 0时，分支周期解是渐近稳定的，当β₂>0时，分支周期解是不稳定的；

(ⅲ) T₂确定分支周期解的周期，当T₂>0时，周期增大，当T₂ < 0时，周期减少.

本节利用MATLAB软件给出具体的数值实例，以补充验证前面给出的理论结果.

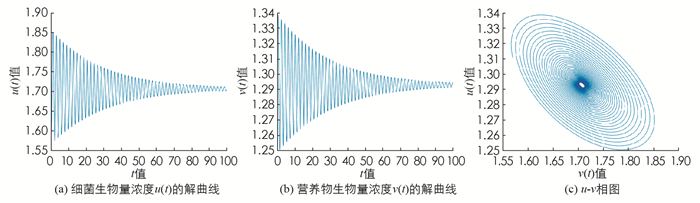
对于系统(5)，设置参数b，K为b=3，K=0.5，则条件$b>1+2 \sqrt{K}$成立，由此可得正常数平衡点为(u^*，v^*)=(1.707 1，1.292 9)，令参数a=9.5满足$0<a<\frac{\left(u^*\right)^2+u^*+K}{K}=10.2426$，则方程(10)存在唯一正根ω₀=3.222 2. 再根据方程(12)，计算可得$\tau_0^j=0.0107+\frac{2 j \pi}{\omega_0}$(j∈$\mathbb{N}$₊). 因此由定理1可知：当τ∈[0，0.010 7)时，正常数平衡点(u^*，v^*)是局部渐近稳定的；当τ∈(0.010 7，+∞)时，正常数平衡点(u^*，v^*)是不稳定的. 且由Hopf分支定理^[2]可知，当$\tau=\tau_0^j=0.0107+\frac{2 j \pi}{\omega_0}$(j∈$\mathbb{N}$₊)时，系统(5)在正常数平衡点(u^*，v^*)处产生Hopf分支.

取τ=0.006 5 < τ₀⁰，由定理1可知系统(5)的正平衡点(u^*，v^*)局部渐近稳定，如图 1.

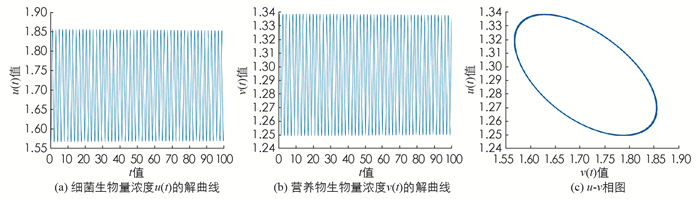
取τ=0.010 7=τ₀⁰，由定理1可知系统(5)在正平衡点(u^*，v^*)处产生Hopf分支，如图 2.

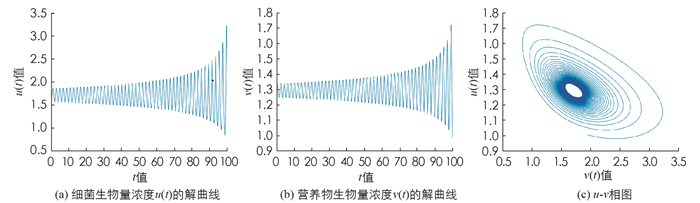
取τ=0.012 1>τ₀⁰，由定理1可知系统(5)的正平衡点(u^*，v^*)是不稳定的，如图 3.

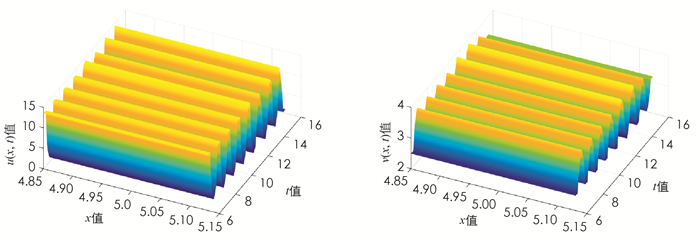
对于系统(13)，设置参数为b=10，K=16，d₁=0.04，d₂=0.5，l=3，且取参数a=3.9满足条件$0<a<\frac{\left(u^*\right)^2+u^*+K}{K}=4.101$，则计算可得正常数平衡点为(u^*，v^*)=(6.561 6，3.438 4)，由定理2可知，当τ=τ_n^j(0≤n≤N₀，j∈$\mathbb{N}$₊)时，系统(13)在正常数平衡点(u^*，v^*)处产生Hopf分支，且由(22)-(24)式计算可得τ₀⁰=0.011 2. 取τ=τ₀⁰=0.011 2和初值u₀(x)=u^*+0.65cos(5x)，v₀(x)=v^*－0.65cos(5x)，则在正常数平衡点(u^*，v^*)附近产生分支周期解，如图 4.