Penalized Expectile Estimationfor High-Dimensional Longitudinal Data

定义随机变量Y的τ-expectile值为

其中τ∈(0，1)，ρ_τ(θ)=|τ-I(θ≤0)|·θ²是非对称平方损失函数，I是示性函数. 由τ-expectile的定义易知，当τ=0.5时，ρ_τ(·)等价于经典的最小二乘损失函数，则模型(1)对应经典的均值回归模型，μ_τ(Y)为随机变量Y的数学期望.

假设有纵向样本数据$\left(y_{i j}, \boldsymbol{X}_{i j}\right), i=1, \cdots, n, j=1, \cdots, m_i$满足如下的expectile线性回归模型

其中：n是个体的数目，m_i是第i个个体的测量次数，y_ij和$\boldsymbol{X}_{i j}=\left(X_{i j}^1, \cdots, X_{i j}^{p_n}\right)^{\mathrm{T}}$是第i个个体的第j次观测值，总观测次数$ N=\sum_{i=1}^n m_i \text {. }$在本文中，协变量的维数p_n可以是发散的. $\boldsymbol\varepsilon_i=\left(\varepsilon_{i 1}, \cdots, \varepsilon_{i m_i}\right)^{\mathrm{T}}$为误差值向量，满足其τ-expectile值μ_τ(ε _i)=0. β_n是p_n维未知参数，值得注意的是，β_n应与τ相关，在不引起混淆的情况下，本文忽略其下标τ. 记$\boldsymbol{y}_i=\left(y_{i 1}, \cdots, y_{i m_i}\right)^{\mathrm{T}}, \boldsymbol{X}_i=\left(\boldsymbol{X}_{i 1}, \cdots, \boldsymbol{X}_{i m_i}\right)^{\mathrm{T}}, $则模型(2)可表示为

对β _n的估计可以通过求解如下目标函数的最小值来获得，即

考虑重复观测时个体内的相关性，文献[13]在纵向数据协变量数固定的情况下提出了GEEE模型，即通过求解如下估计方程

获得系数β _n的估计. 其中，$\mathit{\boldsymbol\Psi}_\tau\left(\boldsymbol{y}_i-\boldsymbol{X}_i \boldsymbol{\beta}_n\right)=\operatorname{diag}\left(\psi_\tau\left(y_{i 1}-\boldsymbol{X}_{i 1}^{\mathrm{T}} \boldsymbol{\beta}_n\right), \cdots, \psi_\tau\left(y_{i m_i}-\boldsymbol{X}_{i m_i}^{\mathrm{T}} \boldsymbol{\beta}_n\right)\right), \psi_\tau(x)=|\tau-\mathrm{I}(x \leqslant 0)|, \hat{\boldsymbol{V}}_{i \tau}=\boldsymbol{A}_{i \tau}^{\frac{1}{2}} \boldsymbol{R}_i\left(\hat{\boldsymbol{\alpha}}_\tau\right) \boldsymbol{A}_{i \tau}^{\frac{1}{2}}, \boldsymbol{A}_{i \tau}=\operatorname{diag}\left(\sigma_{i 1}, \cdots, \sigma_{i m_i}\right), \sigma_{i j}=\operatorname{Var}\left(y_{i j} \mid \boldsymbol{X}_{i j}, \boldsymbol{\beta}_n\right), \boldsymbol{R}_i\left(\boldsymbol{\alpha}_\tau\right)$称为参数为α _τ的工作相关矩阵，用来代替真实的相关系数矩阵，具有独立(IND)，自回归(AR(1))，等相关(CS)，不确定性(UN)相关结构等. $\hat{\boldsymbol{\alpha}}_\tau$是参数α _τ的估计，本文使用矩估计，表达式详见算法过程.

进一步地，本文在协变量维数p_n发散的情况下，提出纵向数据的惩罚非对称最小二乘PGEEE估计，即通过求解如下估计方程

获得系数β _n的PGEEE估计. 其中，$\boldsymbol{P}_{\lambda_n}^{\prime}\left(\left|\boldsymbol{\beta}_n\right|\right)=\left(p_{\lambda_n}^{\prime}\left(\left|\boldsymbol{\beta}_{n 1}\right|\right), \cdots, p_{\lambda_n}^{\prime}\left(\left|\boldsymbol{\beta}_{_np_n}\right|\right)\right)^{\mathrm{T}}, p_{\lambda_n}(t)$是一个含有调节参数λ_n的非负惩罚函数，p′ _λn^(t)为p_λn^(t)的导数. $\operatorname{Sign}\left(\boldsymbol{\beta}_n\right)=\left(\operatorname{sign}\left(\boldsymbol{\beta}_{n 1}\right), \cdots, \operatorname{sign}\left(\boldsymbol{\beta}_{n p_n}\right)\right)^{\mathrm{T}}, \operatorname{sign}(t)=\mathrm{I}(t>0)-\mathrm{I}(t <0)$为符号函数. $\boldsymbol{P}_{\lambda n}^{\prime}\left(\left|\boldsymbol{\beta}_n\right|\right) \operatorname{Sign}\left(\boldsymbol{\beta}_n\right)$定义为对应元素相乘得到的向量. 本文考虑MCP和SCAD两种惩罚方法. MCP惩罚函数的数学表达式为

为简化模型，参考文献[14]，取γ=3. SCAD惩罚函数的数学表达式为

根据文献[2]建议取γ=3.7. 此时模型(6)中需要选择的参数只有λ_n，本文使用BIC准则来选取，表达式见算法过程.

Step1：给定一个λ_n，求解(4)式获得初始值$\hat{\boldsymbol\beta}_n^{(0)}$

Step2：$\hat{\varepsilon}_{i t \tau}=y_{i t}-\boldsymbol{X}_{i t}^{\mathrm{T}} \hat{\boldsymbol{\beta}}_n^{(k)}, $计算相关系数.

Step3：使用如下迭代式计算$\hat{\boldsymbol{\beta}}_n^{(k+1)}:$

其中$\boldsymbol{E}_n\left(\hat{\boldsymbol{\beta}}_n\right)=\operatorname{diag}\left\{\frac{p_{\lambda_n}^{\prime}\left(\left|\hat{\beta}_1\right|+\right)}{\left|\hat{\beta}_1\right|}, \cdots, \frac{p_{\lambda_n}^{\prime}\left(\left|\hat{\beta}_{p_n}\right|+\right)}{\left|\hat{\beta}_{p_n}\right|}\right\} .$

tep4：重复Step2-Step3直至收敛，并计算λ_n对应的BIC值，其表达式为

其中，df表示λ_n对应模型所选择的变量个数.

Step5：重复Step1-Step4，选取BIC值最小的λ_n作为惩罚因子，对应的$\hat{\boldsymbol{\beta}}_n$为未知参数最优解.

记m=max{m_i，i=1，…，n}，参数真值为$\boldsymbol{\beta}_{n 0}=\left(\boldsymbol{\beta}_{n 0(1)}^{\mathrm{T}}, \boldsymbol{\beta}_{n 0(2)}^{\mathrm{T}}\right)^{\mathrm{T}}$不失一般性，设$\boldsymbol{\beta}_{n 0(1)}$为s维非零元素构成的向量，$\boldsymbol{\beta}_{n 0(2)}$为p_n^-s维零向量，$\boldsymbol{\beta}_{n 0(2)}=\bf{0}, $则协变量矩阵可记为$\boldsymbol{X}_i=\left(\boldsymbol{X}_{i(1)}, \boldsymbol{X}_{i(2)}\right), \boldsymbol{X}_{i(1)}=\left(\boldsymbol{X}_{i 1(1)}, \cdots,\right.\left.\boldsymbol{X}_{i m_i(1)}\right), \boldsymbol{X}_{i j(1)}$为$\boldsymbol{X}_{i j}$的前s个元素构成的向量. C，C₁，C₂，…代表与n无关的正常数，不同地方可以取不同的值. 为了证明估计量的性质，本文需要以下假设条件：

(A1) $\sup {i, j}\left\|\boldsymbol{X}_{i j}\right\|=O_p\left(\sqrt{p_n}\right) ;\left\{\left(\boldsymbol{X}_i, \boldsymbol{y}_i\right)\right\}_{i=1}^n$独立，且$\operatorname{Var}\left[\mathit{\Psi}_\tau\left(\boldsymbol{y}_i-\boldsymbol{X}_{i(1)} \boldsymbol{\beta}_{n 0(1)}\right)\left(\boldsymbol{y}_i-\boldsymbol{X}_{i(1)} \boldsymbol{\beta}_{n 0(1)}\right)\right]=\mathrm{E}\left[\mathit{\Psi}_\tau\left(\boldsymbol{y}_i-\boldsymbol{X}_{i(1)} \boldsymbol{\beta}_{n 0(1)}\right)\left(\boldsymbol{y}_i-\boldsymbol{X}_{i(1)} \boldsymbol{\beta}_{n 0(1)}\right)\left(\boldsymbol{y}_i-\boldsymbol{X}_{i(1)} \boldsymbol{\beta}_{n 0(1)}\right)^{\mathrm{T}}\mathit{\Psi}_\tau\left(\boldsymbol{y}_i-\boldsymbol{X}_{i(1)} \boldsymbol{\beta}_{n 0(1)}\right)\right]=\boldsymbol{\Sigma}_{i \tau} ;$存在υ>0，Δ>0，使$\mathrm{E}\left|\psi_\tau\left(\varepsilon_{i j \tau}\right)\right|^{4+υ} <\Delta, \mathrm{E}\left|\varepsilon_{i j \tau}\right|^{4+υ} <\Delta ;$

(A2) 估计协方差阵$\hat{\boldsymbol{V}}_{i \tau}$满足$\left\|\hat{\boldsymbol{V}}_{i \tau}^{-1}-\overline{\boldsymbol{V}}_{i \tau}^{-1}\right\|=O_p\left(\sqrt{\frac{p_n}{n}}\right), $其中$\overline{\boldsymbol{V}}_{i \tau}$是满足$C_1 \boldsymbol{I}_{m_i} \leqslant \overline{\boldsymbol{V}}_{i z} \leqslant C_2 \boldsymbol{I}_{m_i}$的正定阵($\overline{\boldsymbol{V}}_{i \tau}$可以不等于真实协方差阵$V_{i 0 r}$)，I _mi是m_i阶单位阵. $\|\boldsymbol{A}\|=\left[\operatorname{tr}\left(\boldsymbol{A} \boldsymbol{A}^{\mathrm{T}}\right)\right]^{\frac{1}{2}}$表示矩阵A的Frobenius范数；

(A3) 存在两个正常数C₁，C₂，使得$C_1 \leqslant \lambda_{\min }\left(\frac{1}{n} \sum\limits_{i=1}^n \boldsymbol{X}_i^{\mathrm{T}} \boldsymbol{X}_i\right) \leqslant \lambda_{\max }\left(\frac{1}{n} \sum\limits_{i=1}^n \boldsymbol{X}_i^{\mathrm{T}} \boldsymbol{X}_i\right) \leqslant C_2, \lambda_{\min }, \lambda_{\max }$分别表示矩阵的最小和最大特征根；

(A4) 记$\boldsymbol{P}_1=\boldsymbol{P}_{\lambda_n}^{\prime}\left(\left|\boldsymbol{\beta}_{n 0(1)}\right|\right) \operatorname{Sign}\left(\boldsymbol{\beta}_{n 0(1)}\right), \boldsymbol{P}_2=\operatorname{diag}\left(p_{\lambda_n}^{\prime \prime}\left(\beta_{10}\right), \cdots, p_{\lambda_n}^{\prime \prime}\left(\beta_{s 0}\right)\right) ; \boldsymbol{D}_\tau=\lim\limits _{n \rightarrow \infty} \frac{1}{n} \sum\limits_{i=1}^n \boldsymbol{X}_{i(1)}^{\mathrm{T}} \overline{\boldsymbol{V}}_{i \tau}^{-1} \boldsymbol{\Sigma}_{i \tau} \overline{\boldsymbol{V}}_{i \tau}^{-1} \boldsymbol{X}_{i(1)}, \mathit{\boldsymbol\Phi}_\tau=\lim\limits _{n \rightarrow \infty} \frac{1}{n} \sum\limits_{i=1}^n \boldsymbol{X}_{i(1)}^{\mathrm{T}} \overline{\boldsymbol{V}}_{i \tau}^{-1} \mathrm{E}\left[\mathit{\Psi}_\tau\left(\boldsymbol{y}_i-\boldsymbol{X}_{i(1)} \boldsymbol{\beta}_{n 0(1)}\right)\right] \boldsymbol{X}_{i(1)}$

(A5) $\frac{1}{n} p_n^3 \rightarrow 0;$

(A6) $a_n=\max\limits _{1 \leqslant k \leqslant p_n}\left\{p_{\lambda_n}^{\prime}\left(\left|\beta_{j 0}\right|\right), \beta_{j 0} \neq 0\right\}=O\left(n^{-\frac{1}{2}}\right), b_n=\max\limits _{1 \leqslant k \leqslant p_n}\left\{p_{\lambda_n}^{\prime \prime}\left(\left|\beta_{j 0}\right|\right), \beta_{j 0} \neq 0\right\} \rightarrow 0 ;$

(A7) $\liminf \limits_{n \rightarrow \infty} \liminf \limits_{\theta \rightarrow 0+} \frac{p_{\lambda_n}^{\prime}(\theta)}{\lambda_n}>0, \frac{1}{\lambda_n} \sqrt{\frac{p_n}{n}} \rightarrow 0 .$

定理1  记方程(6)的解$\hat{\boldsymbol{\beta}}_n$为模型(2)中系数$\boldsymbol{\beta}_n$的PGEEE估计. 当(A1)-(A7)满足，若$\lambda_n \rightarrow 0, $且当$n \rightarrow \infty$时，$\frac{\sqrt{\frac{p_n}{n}}}{\lambda_n} \rightarrow 0, $那么存在$\hat{\boldsymbol{\beta}}_n=\left(\hat{\boldsymbol{\beta}}_{n(1)}^{\mathrm{T}}, \hat{\boldsymbol{\beta}}_{n(2)}^{\mathrm{T}}\right)^{\mathrm{T}}$满足

(i) (稀疏性) $\hat{\boldsymbol{\beta}}_{n(2)}=\bf{0} ;$

(ii) (渐近正态性) $\sqrt{n}\left(\mathit{\boldsymbol\Phi}_\tau+\boldsymbol{P}_2\right)\left(\hat{\boldsymbol{\beta}}_{n(1)}-\boldsymbol{\beta}_{n 0(1)}+\left(\mathit{\boldsymbol\Phi}_\tau+\boldsymbol{P}_2\right)^{-1} \boldsymbol{P}_1\right) \rightarrow N\left(\bf{0}, \boldsymbol{D}_\tau\right)$

注  定理1表明所提出的方法可以选出正确的模型，同时实现对重要变量回归系数的参数估计，称为Oracle性质^[2].

定理1的证明：

(i) 令$\alpha_n=\sqrt{\frac{p_n}{n}}.$第一步证明相合性，即$\left\|\hat{\boldsymbol{\beta}}_n-\boldsymbol{\beta}_{n 0}\right\|=O_p\left(\sqrt{\frac{p_n}{n}}\right) .$只需证明对任意的$ \epsilon>0 \text {, }$，都存在一个大的常数D，使得

成立即可. 根据表达式，有

计算I的阶. 令$\overline{\boldsymbol{S}}\left(\boldsymbol{\beta}_n\right)=\sum_{i=1}^n \boldsymbol{X}_i^{\mathrm{T}} \overline{\boldsymbol{V}}_{i \tau}^{-1} \mathit{\boldsymbol\Psi}_{\mathrm{\tau}}\left(\boldsymbol{y}_i-\boldsymbol{X}_i \boldsymbol{\beta}_n\right)\left(\boldsymbol{y}_i-\boldsymbol{X}_i \boldsymbol{\beta}_n\right), $有

其中

考虑I₁₁，有

由Cauchy-Schwarz不等式知，$\left|I_{11}\right| \leqslant\left\|\boldsymbol{\beta}_n-\boldsymbol{\beta}_{n 0}\right\|\left\|\overline{\boldsymbol{S}}\left(\boldsymbol{\beta}_{n 0}\right)\right\|=O_p\left(\sqrt{\frac{p_n}{n} \cdot \sqrt{n p_n}}\right)\|u\|=\|u\| O_p\left(p_n\right) .$令$\hat{\boldsymbol{V}}_{i \tau}^{-1}-\overline{\boldsymbol{V}}_{i \tau}^{-1}=\left(q_{i t s}\right)_{1 <t, s <m_i}, $有

且

由(18)式知，$\left|I_{12}\right|=O_p\left(\sqrt{\frac{p_n}{n}} \cdot \sqrt{\frac{p_n}{n}} \cdot \sqrt{n p_n}\right)\|u\|=o_p\left(p_n\right)\|u\| \text {, }$因此

将I₂分为两部分计算，有

记

其中由(A3)知

又因为

由(24)式得，$\left|I_{21}^b\right|=O_p\left(\sqrt{n p_n} \cdot \alpha_n\right)\|u\|=O_p\left(p_n\right)\|u\|, $故$\left|I_{21}\right|=-O_p\left(p_n\right)\|u\|^2+O_p\left(p_n\right)\|u\| .$类似地，计算I₂₂.

其中

又

由(28)式知，$I_{22}^b=O_p\left(\sqrt{p_n} \cdot \alpha_n\right)\|u\|=o_p\left(p_n\right)\|u\|, $则$I_{22}=-o_p\left(p_n\right)\|u\|^2+o_p\left(p_n\right)\|u\| .$因此，有

由(19)，(29)式可得，(14)式的值由(29)式控制，小于0. 易知(13)式中的第二项以$n\;\;{\alpha\;_n}^2\|\;u\;\|\;\;+n \;\;b\;_n \;\alpha\;_n\;^2\;\|\;u\;\|\;^2$为界，因此可以找到一个足够大的D，使得(13)式的值完全由(29)式决定. (12)式得证.

接着证明稀疏性$\hat{\boldsymbol{\beta}}_{n(2)}=\bf{0}$即对于任意$\left\|\boldsymbol{\beta}_{n(1)}-\boldsymbol{\beta}_{n o(1)}\right\|=O_p\left(\sqrt{\frac{p_n}{n}}\right)$，存在$\varepsilon_n=C \sqrt{\frac{p_n}{n}}, j=s+1, \cdots, $p_n, 使得

由相合性证明过程知$\left\|\boldsymbol{S}\left(\boldsymbol{\beta}_n\right)\right\|=O_p\left(\sqrt{n p_n}\right)$因此

由(A7)可知，(31)式的符号完全由β_j的符号决定. (30)式得证.

(ii) 由相合性证明过程知，$\boldsymbol{Q}\left(\left(\boldsymbol{\beta}_{n(1)}^{\mathrm{T}}, \bf{0}^{\mathrm{T}}\right)^{\mathrm{T}}\right)$存在$\sqrt{\frac{n}{p_n}}$相合的局部最小值. 令$\hat{\boldsymbol{\beta}}_n$为局部最小值，则其满足如下方程

即

根据文献[13]可知，$-\frac{1}{n}\left(\mathrm{E}\left[\overline{\boldsymbol{S}}\left(\boldsymbol{\beta}_{n 0(1)}\right)\right]\right)^{\prime} \stackrel{p}{\longrightarrow} \mathit{\boldsymbol\Phi}_{\mathrm{r}}, \frac{1}{\sqrt{n}} \overline{\boldsymbol{S}}\left(\boldsymbol{\beta}_{n 0(1)}\right) \rightarrow N\left(0, \boldsymbol{D}_{\mathrm{r}}\right)$由条件(A4)可知，$I I=n \boldsymbol{P}_1+n \boldsymbol{P}_2\left(\hat{\boldsymbol{\beta}}_{n(1)}-\boldsymbol{\beta}_{n 0(1)}\right)$由Slutsky定理可得

定理证毕.

为了研究所提方法的有限样本性质，本文比较了不同的惩罚方法及相关结构下所提出方法的效果. 数据来源于以下模型

对于协变量的生成分为两步：第一步，生成$\boldsymbol{Z}_{i j}=\left(Z_{i j}^1, \cdots, Z_{i j}^{p n}\right)^{\mathrm{T}}, $来源于多元正态分布N(0，R _pn)，$\left(\boldsymbol{R}_{p_n}\right)_{a, b}=0.5^{|a-b|}, 1 \leqslant a, b \leqslant p_n .$第二步，令$X_{i j}^l=Z_{i j}^l, l \neq k, X_{i j}^k=F\left(Z_{i j}^k\right), $生成p_n维向量$\boldsymbol{X}_{i j}^{\mathrm{T}}=\left(X_{i j}^1, \cdots, X_{i j}^{p_j}\right), F(\bullet)$表示标准正态分布的分布函数，主要用于刻画数据中的异方差. $\varepsilon_i^{\mathrm{T}}=\left(\varepsilon_{i 1}, \cdots, \varepsilon_{i m_i}\right)$服从多元正态分布N(0，R_i). 分别考虑如下三种情形：

情形1   $p_n=10, k=9, m_i=4, n=50, 100, 200, \boldsymbol{\beta}_n=(-3, 5, 0, 0, 4, 0, 0, 2, 0, 0)^{\mathrm{T}}. \boldsymbol{R}_i$是参数为0.9的等相关结构矩阵.

情形2   k=2，m_i服从参数为(3，6)的均匀分布，R _i是参数为0.9的AR(1)结构矩阵. 其余设置和情形1一样.

情形3  p_n=30，n=100，200. β _n =(-3，5，0，0，4，0，0，2，0，0，…，0)^T. 其余设置和情形1一样.

注  在情形1和情形3中，τ=0.5时，真实模型中的自变量为$X_{i j}^1, X_{i j}^2, X_{i j}^5, X_{i j}^8 ; \tau=0.9$时，真实模型中的自变量为$X_{i j}^1, X_{i j}^2, X_{i j}^5, X_{i j}^8, X_{i j}^9$. 情形1与情形3的设置可以比较在不同的τ下PGEEE选择的模型，同时观察协变量维数增加时的模型估计效果. 情形2中，无论τ取何值，真实模型中的自变量均为$X_{i j}^{1 i}, X_{i j}^2, X_{i j}^5, X_{i j}^8$但部分回归系数与τ有关. τ=0.5时，β₂=5；τ=0.9时，β₂=6.29. 情形2的设置可以比较PGEEE在不同τ水平下的估计精度.

重复模拟100次，表 1-3给出了3种情形下MCP和SCAD两种惩罚方法的PGEEE估计结果. 使用指标Size(平均选取变量个数)，FN(重要变量被误认为噪音变量的平均个数)，FP(噪音变量被选择的平均个数)，Prob(X_ij⁹被选出的概率)，MSE(估计量的均方误差)，MAE(回归系数β₂估计量的平均绝对误差)来衡量估计量的优劣. 模拟结果显示：

(i) SCAD和MCP两种惩罚方法并无明显的优劣之分. FN均为0，表示所有重要的变量都被识别，FP接近0，表明噪音变量被选择的可能性很小；

(ii) 在情形1和情形3中，τ=0.9时，Prob等于1，而τ=0.5时，Prob的值接近0. 这表明所提出的估计量PGEEE可以在不同的τ水平下，有效识别出正确的模型，刻画数据中的异方差结构；

(iii) 在不同的τ水平下，即使选择的变量相同，参数估计值也可能不同(情形2). 在此情形下，估计量的MSE和MAE随着样本量增大而减小，表示该方法可以在识别出异方差的同时实现回归参数的一致估计；

(iv) 对比情形1和情形3，协变量维数p_n从10增加至30，结果显示模型中噪音变量数量增加时，PGEEE估计表现依然较好，且估计量MSE减小，表明该方法可以用于分析高维数据，排除无关变量，识别出重要变量.

(v) 考虑相关结构时估计量的表现总体上优于独立(IND)的情形. 即使相关结构被误判后，参数估计效果依然很好，尤其使用UN结构时.

数据来自1976年至1982年间对美国经济收入动态的面板研究，包含了连续7年595名民众的工资水平，属于平衡数据，更多详细信息参考文献[15]. 该研究中，协变量包括工作经历E，工作时间W，工作职业O(蓝领取1，否则0)，工作行业I(制造业取1，否则0)，居住地S(居住在南部取1，否则0)，种族B(黑人取1，否则0)，是否住在都市统计区A(如果是取1，否则0)，是否结婚M(结婚取1，否则0)，性别F(女性取1，否则0)，劳动保障U(签合同取1，否则0) 及受教育程度D，响应变量为对数变换后的工资水平.

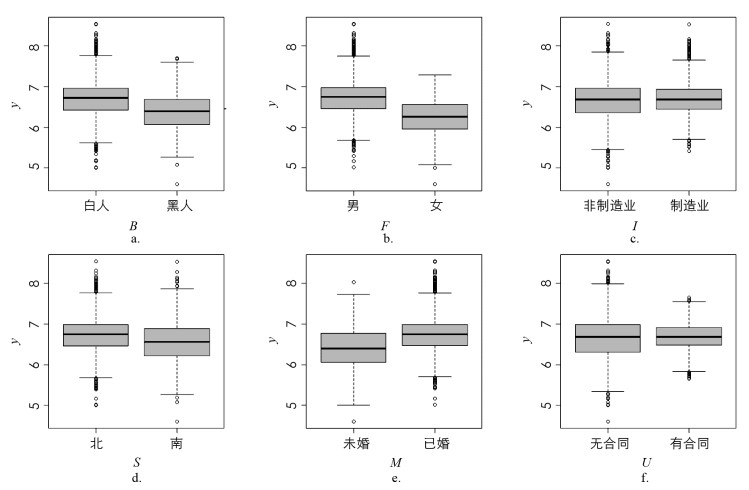
表 4给出了τ=0.01，0.5，0.95下参数的PGEEE估计，其中τ=0. 5对应经典的均值回归估计. 分析结果可知，不同的惩罚方法和不同的相关结构选出的变量基本一致. 可以看到，在3个水平下均被选择的变量有O，B，F，D；均未被选择的变量有W. 截距项，B，F的系数估计随着τ不同而变化，图 1a，b为不同种族及性别对应的工资随时间变化的箱线图. 男性的工资明显高于女性，白人的工资明显高于黑人. 在τ=0.01时，E被认为是噪音变量，而在τ=0.5和0.95时被认为是重要变量. 在τ=0.95时，除了独立结构下MCP估计外，工作行业I，居住地S，是否结婚M，劳动保障U均被剔除在模型外；而在τ=0.01和0.5时则被认为是重要变量. 图 1c，d, e, f为这些变量对应的工资分布箱线图. 以变量S为例，可以看到，在低分位点时，居住在北部的工资要明显高于南部，但是在高分位点时，两者的区别并不明显，这与PGEEE的估计结果相吻合. 由此可见，该方法比采用普通最小二乘估计(τ=0.5)挖掘出了更多的信息

本文基于expectile提出了高维纵向数据的PGEEE估计量，在实现模型变量选择的同时，对模型的回归系数进行估计. 在正则条件下本文建立了PGEEE估计量的Oracle性质. 数值模拟结果显示，MCP与SCAD惩罚及不同的协方差结构在变量选择方面并无明显差异. 相较于独立结构，考虑相关结构时回归系数的估计效率更高. 多数情况下，不确定结构(UN)的PGEEE估计量具有较好的估计精度. 最后建立工资数据的PGEEE模型，可以看到在不同的τ水平下，影响工资的因素有所区别，同一个因素影响程度也可能不同. 这表明PGEEE可以有效识别数据中的异质结构，比经典的惩罚估计方程估计(PGEE)挖掘出更丰富的信息，更合理地分析了工资的影响因素.