-
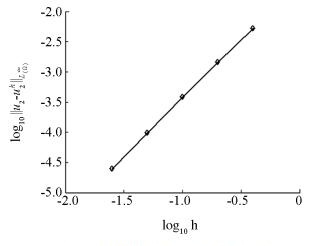
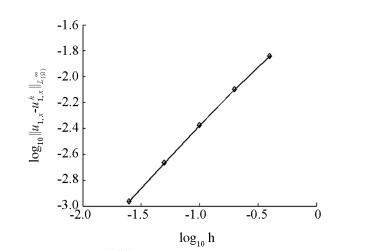
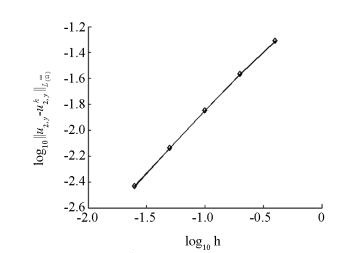
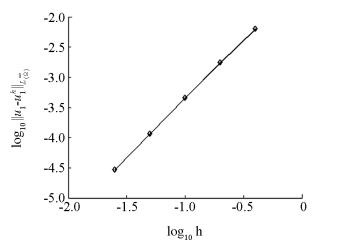
移动最小二乘近似是形成无网格方法逼近函数的重要方法之一[1-2], 然而由于其形成的无网格方法需要选取较多的节点, 程玉民等人提出了复变量移动最小二乘近似[3], 该方法使用一维变量构造二维问题的形函数, 可以克服二维问题中移动最小二乘近似形成的无网格方法配点过多的问题.文献[4-10]讨论了移动最小二乘近似的逼近误差, 文献[11]讨论了有限点法的误差, 文献[12]对于改进的移动最小二乘近似在Sobolev空间中的误差分析做了相应的工作, 文献[13]分析了插值型移动最小二乘近似的逼近误差.无网格法作为一种新兴的数值计算方法, 已经被广泛地应用于工程计算领域[14-15].以上这些成果都极大地丰富了无网格法的理论, 然而基于复变量移动最小二乘近似的无网格方法的基本理论还很不完善.本文在以上工作的基础上, 讨论了复变量移动最小二乘近似的逼近误差, 分析结果表明逼近误差随着节点间距的减小而降低, 数值算例验证了结论的正确性.本文的结果为基于复变量移动最小二乘近似的无网格方法的理论研究提供了基础.
全文HTML
-
复变量移动最小二乘近似是对向量函数的逼近, 取试函数
其中, uh(z)是对函数u(z)=u1(z)+iu2(z)的逼近, PT(z)=(p0(z), p1(z), …, pm(z))是取自多项式空间的基函数.一般地, 可选取基函数为
在点z的局部逼近定义为
aj(z)为待求, 由下面定义的泛函J取极小值得到:
zi为点z的紧支域内的节点, w(z)为具有紧支特性的权函数, z1, z2, …, zn⊂Ω⊂
$\mathbb{C}$ )2为一个点集, 我们用表示节点间距, R=sh表示节点影响域半径, 其中s为一个固定常数, 其决定了覆盖计算点的节点个数.且有
(3) 式可以写成如下的矩阵形式:
其中:
为了求得α(z), 对J取极值, 可得
其中:
因此我们有
复变量移动最小二乘近似是基于节点的近似, 假设待求函数在节点处的函数值已知, 通过构造的泛函使得逼近函数在这些节点处的误差的加权平方和最小, 从而求出待求函数在求解域内的全局近似.
逼近函数uh(z)可以写成如下形式:
其中
最后, 可以得到:
-
为了估计误差, 我们首先做如下的假设:
(ⅰ)对∀z∈Ω, 存在与h无关的正整数K1和K2, 使得m+1≤K1≤n≤K2, 即影响域包含计算点的节点个数至少是K1个, 至多是K2个;
(ⅱ)存在与h无关的常数c0>0, 使得对∀z∈
${B_{\frac{R}{2}}}$ (0), 都有w(z)≥c0;(ⅲ)存在cp, 使得
$\frac{h}{\delta }$ ≤cp, 其中δ=min|zi-zj|;(ⅳ)w∈C1(BR(0))∩W1, ∞(Ω), 存在c1, 使得
${\left\| {\mathit{w'}} \right\|_{{L^\infty }\left( \mathit{\Omega } \right)}} \le \frac{{{c_1}}}{h}.$ 引理1[5] 若假设(ⅰ)成立, 且uh(z, z)由(2) 式确定, 则对∀u∈Cm+1(Ω), u(z)-uh(z, z)关于z在BR(z)∩Ω内至少有m+1个根.
推论1 u1h(z, z)-u1(z)和u2h(z, z)-u2(z)在BR(z)∩Ω内至少有m+1个根.
因此, 由插值误差估计, 有下面的定理1成立:
定理1[13] 若上述假设成立, 且u(z)∈Cm+1(Ω), 则存在常数C=C(m), 使得对∀z∈Ω和∀z∈BR(z)∩Ω, 都有
特别地, 当z=z时, 有
同理, 对u2h(z, z)-u2(z)有相同的估计.
注1 本文中的字母C表示与h无关的常数, 每次出现时可能并不相同.这里要强调的是其与h无关.
定理1得到的是逼近函数的误差估计, 下面估计逼近函数一阶偏导数的误差, 为此要估计
$\frac{{\partial {{\bar u}^h}}}{{\partial x}} - \frac{{\partial \bar u}}{{\partial x}}$ 的误差, 本文只讨论实部偏导的逼近误差, 虚部偏导的逼近误差同理可以证明.在此之前, 先给出如下的引理:引理2 若u∈Cm+1(Ω), z∈Ω, 使得
$\frac{{\partial u_{^1}^h\left( {\mathit{z}, \mathit{\bar z}} \right)}}{{\partial z}}$ 存在, 且假设(ⅰ)-(ⅳ)成立, 则存在常数C=C(c0, c1, cp, m), 使得对∀z∈BR(z)∩Ω, 都有证 给定z∈Ω, 由假设(ⅰ)知, 存在m+1个点zj1, zj2, …, zjm+1∈BR(z), 对∀l>0, 定义
根据假设(ⅲ)可以得到
定义
且Q(z)的阶数不大于m, 由于最小值在u1h(z, z)处取到, 故有
所以(18) 式可以化为
对足够小的l>0, 存在θk, 使得
代入(20) 式可得
由
以及假设(ⅳ)可以得到
由定理1可以得到
于是(21) 式化为
由于Q(z)是阶数不超过m的多项式, 所以有
其中lk(z)是拉格朗日多项式基函数, 故有
由假设(ⅲ)可知
由霍尔德不等式以及(22) 式可以得到
不等式两边同时除去
$\sum\limits_{k \notin \left\{ {{j_i}} \right\}} {\left| {Q\left( {{z_k}} \right)} \right|} $ , 可以得到由(23) 以及(24) 式可以得到, 对∀z∈Bh(z)∩Ω, 都有
定理2 令u∈Cm+1(Ω), 且假设(ⅰ)-(ⅳ)成立, 则存在常数C=Cc0, c1, cp, m, 使得有如下关系式成立:
证 由于权函数一阶连续可微, 且基函数无穷阶可微, 因此uh(z, z)处处连续可微, 即u1h(z, z)∈W1, ∞(Ω).我们要估计
根据链式法则, 有
所以要估计的式子变为
由于u1h(z, z)-u1(z)在BR(z)∩Ω内至少有m+1个根, 因此
$\frac{{\partial {u_1}\left( {\mathit{\bar z}} \right)}}{{\partial \bar z}}{\rm{ - }}\frac{{\partial u_1^h\left( {\mathit{z, \bar z}} \right)}}{{\partial \bar z}}$ 在BR(z)∩Ω内至少有m个根, 因此由插值误差估计可得由引理1可以得到
由(27), (28) 及(29) 式可得
在(30) 式中取z=z, 定理2得证.
下面的定理3说明
$\frac{{\partial u_1^h}}{{\partial x}} - \frac{{\partial {u_1}}}{{\partial x}}$ 和$\frac{{\partial u_1^h}}{{\partial y}} - \frac{{\partial {u_1}}}{{\partial y}}$ 的误差与$\frac{{\partial u_1^h}}{{\partial z}} - \frac{{\partial {u_1}}}{{\partial z}}$ 的误差保持一致.定理3 若u∈Cm+1Ω, 假设(ⅰ)-(ⅳ)成立, 则存在常数C=C(c0, c1, cp, m), 使得对于∀z=x+iy∈Ω, 都有:
证因为:
因此有:
-
本文在对权函数做出适当假设的基础上, 得到了复变量移动最小二乘近似逼近函数及其偏导的误差估计, 结果表明, 误差随节点间距的减小而降低.



 下载:
下载: