三峡库区位于长江上游下段，西起重庆江津区，东至湖北宜昌市，覆盖了重庆市所辖22个县(区)和湖北省所辖4个县.万州区位于四川盆地东部，地处渝东北、三峡库区腹心，濒临长江三峡，跨大巴山、巫山、七曜山和盆东平行岭谷区，境内低山丘陵的面积约占总面积的1/4.该区属于亚热带季风湿润气候，温和多雨，多年平均降水在1 000 mm以上.万州气象观测站地理坐标为东经108°24′，北纬30°46′，观测海拔为186.7 m.

本文所用的数据来源于国家气象数据共享网(http://cdc.gov.cn/index.jsp.)，选取三峡库区内万州区气象站点1955-2014年的月降水数据.

线性回归是利用线性回归方程中的最小二乘函数对自变量和因变量之间关系进行建模的一种回归分析方法.本文采用的一元线性回归分析，用时间序列作为自变量x，降水序列作为因变量y，建立一元线性回归方程：

式中：斜率b表示气候倾向率，用于定量分析降水的线性变化趋势.

小波分析方法是在20世纪中后期逐渐发展起来的一种数学方法，被认为是传统傅里叶分析方法的突破进展^[13].小波分析能够清晰地揭示出隐藏在时间序列中的多种变化周期，小波变换的结果可以反映出系统在不同时间尺度中的变化趋势，这些年被广泛应用于气候的多尺度分析研究中^[14-16].本文采用Morlet小波分析方法对三峡库区的降水序列进行连续小波变换，利用Matlab软件作出小波系数实部图和小波方差图，进而分析得出三峡库区降水的多时间尺度变化特征.

R/S分析法，也称重标极差分析法，最初是由英国水文学家Hurst在20世纪50年代研究尼罗河多年水文观测资料时提出来的，后来又经过Mandelbrot和Wallis等多人的努力逐步完善，发展成为研究时间序列的分形理论^[17]. Hurst在研究中使用R/S分析法，并引入了一个新的统计量，即Hurst指数.通过对Hurst指数的结果分析，可以预测时间序列未来的持续性或反持续性趋势^[18].本文基于R/S分析法，利用SPSS软件对过去60年降水序列的Hurst指数进行计算，以预测三峡库区未来的降水趋势.

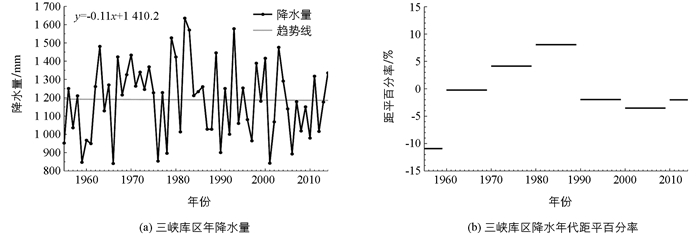
由图 1(a)可知，三峡库区降水序列的气候倾向率为-0.11 mm/a，由此说明降水量总体上的线性减少趋势无统计学意义，但年际和年代际波动较大.这60年来年降水量的变化范围在800~1 700 mm之间，多年平均降水量为1 189.2 mm，其中年降水量最大值为1982年的1 635.2 mm，年降水量最小值为1966年的840.7 mm，二者相差794.5 mm.三峡库区年降水量最大值约为最小值的1.9倍，说明三峡库区有明显的丰水年和枯水年，而1982年的最大降水量直接导致了当年长江水位居高不下，引发特大洪灾.

图 1(b)是三峡库区年降水量年代距平百分率变化图，结合表 1各年代际变化数据可知，整个年代际内降水距平百分率除1955-1959年外，其余都在正负10%以内，说明各年代降水整体变化不大，都在平均值附近波动.根据各年代的距平值，三峡库区在20世纪50年代中期至60年代为少雨期，其中1966年降水量达到最小值，比平均值少348.5 mm；70年代至80年代为多雨期，其中1982年降水量达到最大值，比平均值多446 mm，而在90年代至21世纪初期降水又有所减少.

根据这60年来的年降水变化可知，三峡库区年降水量整体上呈现不明显的减少趋势，降水的年际和年代际变化较大，这60年间三峡库区降水在各年代的变化趋势为“少-多-少”.该区的降水趋势与四川盆地年降水量减少的趋势相符^[19]，与整个重庆地区的年降水量变化趋势保持一致^[7].

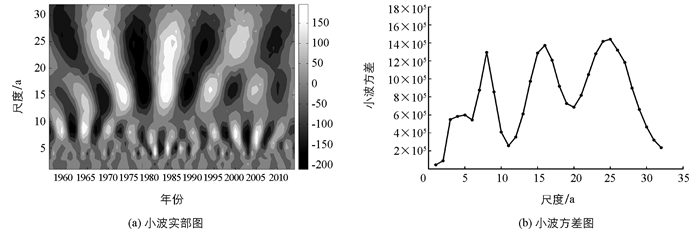
为了能够提取出降水序列的实际波动，本文采用年降水的距平值进行分析. 图 2是1955-2014年三峡库区年降水距平值的小波分析图，反映了三峡库区近60年来降水量在多个特征时间尺度上的周期变化及其在时间域中的分布状况. 图 2(a)是小波系数实部等值线图，小波系数实部值为正时，代表降水丰富；小波系数实部值为负时，降水偏少.图中用灰度表示，颜色越深代表降水越少，而等值线闭合中心则对应降水丰欠中心.

小波系数实部图形成多个尺度正负相间的震荡中心，显示出三峡库区近60年降水量存在多个不同尺度的周期变化.总的来说，以10年特征时间尺度为界，图的上半部分等值线较为稀疏，对应较长尺度周期的震荡(低频振荡)，而下半部分等值线相对密集，对应较短尺度周期的震荡(高频震荡).整个降水变化过程中主要存在(5~8)，(13~16) 和准25年的3类尺度的周期，这三类尺度的周期变化具有全域性，在整个分析时段表现的非常稳定，5~8年的尺度存在多次丰欠震荡，13~16年的尺度存在5次丰欠震荡，而准25年尺度上存在“少-多-少-多-少-多-少”的3次震荡.此外，1980年左右降水出现了5年尺度的变化，存在4次震荡，但在1990年之后就消失了，说明5年尺度的变化比较局限.

图 2(b)是小波方差图，能反映时间序列波动能量随时间尺度的分布情况，对应峰值处的尺度为时间序列的主要时间尺度，可以用来确定降水变化过程中存在的主周期.三峡库区近60年降水距平序列的小波方差图中存在3个较为明显的峰值，依次对应着8，16和25年.其中8年时间尺度、16年时间尺度和25年时间尺度对应的峰值都比较大，25年时间尺度的小波方差值最大，说明其震荡能量最强、变化周期最明显，为第一主周期；16年时间尺度次之，为第二主周期；8年时间尺度最小，为第三主周期.此外，5年尺度虽然也对应一个峰值，但相比于另外3个尺度，其峰值较低，不计为主周期.

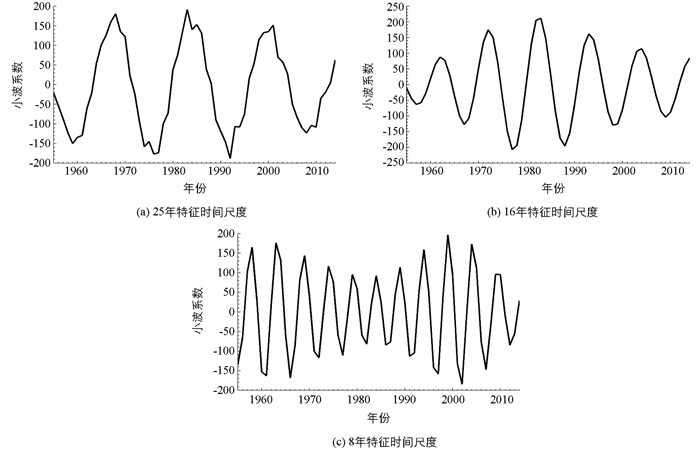
根据小波方差检验的结果，我们绘制出了控制三峡库区年降水变化特征的25，16和8年3个主周期的小波系数图(图 3).

从主周期趋势图中我们可以分析出在不同的时间尺度下，三峡库区年降水量存在的平均周期以及丰欠交替特征.在25年特征时间尺度上(图 3(a))，降水量变化大约经历了3个周期的丰欠交替，其变化的平均周期为20年左右.在16年特征时间尺度上(图 3(b))，降水量变化大约经历了5次周期的丰欠变化，其变化的平均周期为12年左右.在8年特征时间尺度上(图 3(c))，降水量变化大约经历了11个周期的丰欠转换期，其变化的平均周期为5.5年左右.由此可见，时间尺度越小，降水震荡越频繁，平均变化周期越短.

小波分析的结果显示出，三峡库区近60年来的降水变化特征主要是由25，16和8年这3个时间尺度的周期所控制.与前人的研究相比，周浩等^[7]对重庆近46年来的气候变化进行了分析，得出重庆市降水变化周期基本在10年以内，没有明显的年代际尺度周期，而本文基于更长时间的降水量，发现了25年和16年的年代际尺度变化.此外，刘晓冉等^[20]结合重庆30个台站的资料进行研究，发现重庆降水存在准15年的周期震荡，本文得出的16年周期与之相差1年，表明所得周期分析结果是可信的.

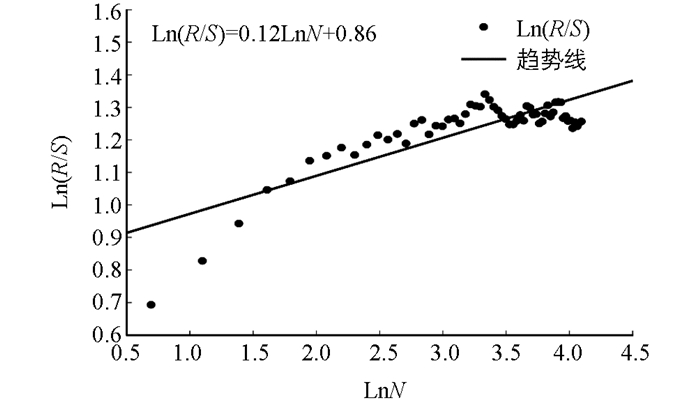
由R/S分析法得出Hurst指数，具体计算原理可参照文献[21]. 1955-2014年三峡库区的降水序列共有60个数值，将降水序列分成K个长度为N(N依次取值为2，3，4…60) 的子序列，分别计算各子序列的极差R和标准差S，再计算R和S的比值，取N和R/S的对数，对LnN和Ln(R/S)用最小二乘法求出Hurst指数.

Hurst指数取值为0~1，不同的Hurst指数具有不同的意义^[22]：

1) 当Hurst指数为0.5时，表明时间序列为相互独立、方差有限的随机序列，前后的变化无关；

2) 当Hurst指数在0~0.5之间时，表明时间序列存在负相关关系，意味着时间序列未来的变化与过去具有反持续性，指数越小，反持续性越强；

3) 当Hurst指数在0.5~1之间时，表明时间序列呈正相关，意味着时间序列具有可持续性，未来的变化与过去一致.

结合Hurst指数的含义，由图 4可得，三峡库区降水序列的Hurst指数为0.12，数值在0~0.5之间，说明未来的降水将呈现与过去相反的趋势.根据表 1得出各年代降水“少-多-少”的变化趋势，预计三峡库区未来年降水可能会出现相对增多趋势，与刘晓冉等^[11]预测三峡库区年降水在21世纪总体上将增加的趋势相吻合，与张天宇等^[12]预测三峡库区极端降水增加密切相关.

1) 根据年降水趋势图和距平值变化图，近60年来三峡库区年降水总体上呈微弱的线性减少趋势，虽然整体变化不明显，但年际和年代际波动较大. 20世纪50年代至60年代为少雨期，70年代至80年代为多雨期，90年代至21世纪为少雨期，各年代降水量总体呈现为“少-多-少”的变化趋势.三峡库区的年降水变化与四川盆地和整个重庆地区的年降水减少的趋势相符合.

2) 小波分析结果表明，三峡库区年降水具有明显的多尺度周期变化，年降水主要存在25，16和8年时间尺度的变化.时间尺度越小，降水震荡越频繁，平均变化周期越短.时间尺度25年的年降水变化平均周期为20年；时间尺度16年的平均周期为12年；时间尺度8年的平均周期为5.5年.时间尺度16年和8年都与已有研究相印证，但更大的尺度25年仍存在不确定性，说明对气候特征的研究需要更长时间和更全面的数据资料，才能更好地反映出气候序列的周期变化特征.

3) 由R/S分析法可以得出，Hurst指数在0~0.5之间，说明降水序列未来的变化具有反持续性，即未来的变化将与过去相反.根据过去60年的年代变化趋势，预计未来的一段时间内，三峡库区年降水将会进入相对多雨的阶段，张天宇等^[12]通过研究1961-2007年三峡库区最大连续5天降水的变化规律，预测在未来气候背景下三峡库区极端降水将呈现增加趋势，说明三峡库区年降水的增加极有可能是源于极端降水.

以上结论表明，三峡库区的年降水量变化波动较大，这与其特殊的地理位置密不可分.西有青藏高原，南有印度洋，再加上本身的复杂地形，降水可能会受到青藏高原、夏季风和副热带高压等多种因素的综合影响^[23].本文利用万州区近60年来的降水数据分析了三峡库区过去的降水变化和周期特征，预测未来的年降水量将增多，但未来降水的具体变化和年内分配状况等还不明确，今后还有待于利用降水日数和降水强度以及四季降水量等资料对降水进行更为精细的研究.