高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

基于多形性胶质母细胞瘤的关键基因筛选研究

, 

上一篇

下一篇

夏苑, 全海金. 基于多形性胶质母细胞瘤的关键基因筛选研究[J]. 西南大学学报（自然科学版）, 2017, 39(10): 119-124. doi: 10.13718/j.cnki.xdzk.2017.10.017
引用本文: 夏苑, 全海金. 基于多形性胶质母细胞瘤的关键基因筛选研究[J]. 西南大学学报（自然科学版）, 2017, 39(10): 119-124. doi: 10.13718/j.cnki.xdzk.2017.10.017
shu
Yuan XIA, Hai-jin QUAN. Research on Screening the Key Genes for GBM (Glioblastoma Multiforme)[J]. Journal of Southwest University Natural Science Edition, 2017, 39(10): 119-124. doi: 10.13718/j.cnki.xdzk.2017.10.017
Citation: Yuan XIA, Hai-jin QUAN. Research on Screening the Key Genes for GBM (Glioblastoma Multiforme)[J]. Journal of Southwest University Natural Science Edition, 2017, 39(10): 119-124. doi: 10.13718/j.cnki.xdzk.2017.10.017
shu

基于多形性胶质母细胞瘤的关键基因筛选研究

  • 1.

    西南大学 经济管理学院, 重庆 400715

  • 2.

    西南大学 数学与统计学院, 重庆 400715

  • 基金项目: 国家自然科学基金项目（20130695）
详细信息
    作者简介:

    夏苑(1980-), 女, 四川南溪人, 博士研究生, 主要从事生物信息学和数据挖掘方向的研究 .

  • 中图分类号: TP399

Research on Screening the Key Genes for GBM (Glioblastoma Multiforme)

  • 1.

    School of Economics and Management, Southwest University, Chongqing 400715, China

  • 2.

    School of Mathematics and Statistics, Southwest University, Chongqing, 400715, China

  • 摘要: 多形性胶质母细胞瘤（GBM）是一种最常见且致死率极高的脑部肿瘤.为了解决传统生存模型不能处理变量p远大于样本数n的基因表达数据的缺点，本文构建了一个关键基因筛选算法——SSLC算法.该算法结合限制性优化算法和生存模型筛选出了与生存时间相关的GBM关键基因，并通过比较证明了此算法优于传统经典算法，最后通过文献查找证明筛选出的部分基因是已经证实的和GBM高度相关的基因，为GBM的靶向制药打下基础.
    Abstract: Glioblastoma multiforme (GBM) is one of the most commonly-seen and deadly brain cancer. The traditional survival model has the disadvantage that it cannot process gene expression data in which the variable number P is far greater than the sample number N. In order to solve the problem, this paper constructs a novel algorithm (SSLC) to screen key genes of GBM patients. By combining the constrained optimization method with the survival model, SSLC can select the GBM key genes related to survival time. By comparison, this algorithm has been proved to be superior to the traditional classical algorithm. Literature search shows that some genes screened by the algorithm are highly related to GBM genes. It is hoped that the results of this study may help to lay a foundation for GBM target drug research.
  • 加载中

  • 图 1  SSLC算法流程图

    下载: 全尺寸图片 幻灯片

    图 2  SSLC算法和CoxLasso算法的ROC曲线比较

    下载: 全尺寸图片 幻灯片

    图 3  SSLC算法和CoxLasso算法的AUC曲线比较

    下载: 全尺寸图片 幻灯片

    表 1  GBM基因表达数据集

    数据集 原站点 数据量
    GBM DANA-FARBER CANCER INSTITUTE 2
    GBM NABTT/H. LEE MOFFITT CANCER CENTER 30
    GBM HENRY FORD HOSPITAL (RETRO) 62
    GBM M. D. ANDERSON CANCER CENTER 6
    GBM MSKCC/NEW YORK 2
    GBM NABTT/HENRY FORD HOSPITAL 7
    GBM NABTT/JOHNS HOPKINS 2
    GBM NIH NEURO-ONCOLOGY BRANCH 48
    GBM TJU 30
    GBM UCLA SCHOOL OF MEDICINE 7
    GBM UCSF 17
    GBM UNIV OF PITTSBURGH 9
    GBM UNIVERSITY OF WISCONSIN 5
    下载: 导出CSV

    表 2  CoxLasso算法和SSLC算法结果

    算法 关键基因
    CoxLasso算法 ARIH2 ZNF786 AEBP1 FOXG1 INTS1 GDNF CUTC SGCD CCM2 IL17RC EIF3A CBLN1
    SSLC算法 GDNF KLHL2 GPD1L ADARB2 CLASP2IL17RC FOXD1 ATRNL1 ADAMTS5 SLC35D1 SNTB1 CACNB3 UBAP2L AKAP11 HDAC4 AEBP1 MALSU1 MDK LAMB2 ATE1 CUTC EIF3A SGCD DBC1 LAMA5 CHST12 MOGS FUT9
    下载: 导出CSV
  • [1] GLADSON C L, PRAYSON R A, LIU W M. The Pathobiology of Gliomatumors[J]. Annu Rev Pathol, 2010, 5:33-50. doi: 10.1146/annurev-pathol-121808-102109
    [2] doi: http://pubmedcentralcanada.ca/pmcc/articles/PMC5278190/ LONG H, LIANG C, ZHANGX, et al. Prediction and Analysis of Key Genes inGlioblastoma Based on Bioinformatics[J]. Biomed Res Int, 2017, 2017:7653101.
    [3] TANG N Y, CHUEH F S, YU C C, et al. Benzyl Isothiocyanate Alters the Gene Expression with Cell Cycle Regulation and Cell Death in Human Brain Glioblastoma GBM 8401 cells[J]. Oncology Reports, 2016, 35(4):2089-2096. doi: 10.3892/or.2016.4577
    [4] doi: http://www.ncbi.nlm.nih.gov/pubmed/28365935 LU X, WANG J, SHAN X, et al. Selecting Key Genes Associated with Ovarian Cancer Based on Differential Expression Network[J]. J BUON, 2017, 22(1):48-57.
    [5] WOOD S N. Thin Plate Regression Splines[J]. Journal of the Royal Statistical Society:Series B (Statistical Methodology), 2003, 65(1):95-114. doi: 10.1111/rssb.2003.65.issue-1
    [6] 陈东. 癌症基因微阵列分类方法的研究[D]. 长沙: 湖南大学, 2012.http://cdmd.cnki.com.cn/Article/CDMD-10532-1013170455.htm
    [7] ANDERSEN P K, GILL R D. Cox's Regression Model for Counting Processes:A Large Sample Study[J]. The Annals of Statistics, 1982, 10(4):1100-1120. doi: 10.1214/aos/1176345976
    [8] TIBSHIRANI R. The Lasso Method for Variable Selection in the Cox Model[J]. Statisticsin Medicine, 1997, 16(4):385-395. doi: 10.1002/(ISSN)1097-0258
    [9] 卢涛, 万永静, 杨威.基于稀疏主成分分析和自适应阈值选择的图像分割算法[J].计算机科学, 2016, 43(7):95-100. doi: 10.11896/j.issn.1002-137X.2016.07.016
    [10] 刘传山.基于参数设计字典的稀疏表示方法[J].西南大学学报(自然科学版), 2014, 36(7):156-161. doi: http://youxian.cnki.com.cn/yxdetail.aspx?filename=JXXB20170918003&dbname=CAPJ2015
    [11] PEPE M S. An Interpretation for the ROC Curve and Inference Using GLM Procedures[J]. Biometrics, 2000, 56(2):352-359. doi: 10.1111/j.0006-341X.2000.00352.x
    [12] doi: http://europepmc.org/abstract/MED/20647036 SALETTA F, RAHMANTOYS, RICHARDSON D R. The Translational Regulator eIF3a:The Tricky eIF3 Subunit[J]. Biochim Biophys Acta, 2010, 1806(2):275-286.
    [13] doi: http://pubmedcentralcanada.ca/pmcc/articles/PMC4237223/ PARAJULI P, MITTAL S. Role of IL-17 in Glioma Progression[J]. Journal of Spine & Neurosurgery, 2013(Suppl1):S1-004.
    [14] doi: http://europepmc.org/abstract/MED/9614243 YU T, SCULLY S, YU Y, et al. Expression of GDNF Family Receptor Components During Development:Implications in the Mechanisms of Interaction[J]. Journal of Neuroscience the Official Journal of the Society for Neuroscience, 1998, 18(12):4684-4696.
    [15] doi: http://europepmc.org/abstract/MED/11738825 RO H S, KIM S W, WU D, et al. Gene Structure and Expression of the Mouse Adipocyte Enhancer-Binding Protein[J]. Gene, 2001, 280(1/2):123-133.
    [16] doi: http://pubmedcentralcanada.ca/pmcc/articles/PMC1449517/ ZHANG L, REIDY S P, NICHOLSON T E, et al. The Role of AEBP1 in Sex-Specific Diet-Induced Obesity[J]. Mol Med, 2005, 11(1-12):39-47.
  • 加载中
图( 3) 表( 2)
计量
  • 文章访问数:  1170
  • HTML全文浏览数:  735
  • PDF下载数:  174
  • 施引文献:  0
出版历程
  • 收稿日期:  2017-03-16
  • 刊出日期:  2017-10-20

基于多形性胶质母细胞瘤的关键基因筛选研究

    作者简介: 夏苑(1980-), 女, 四川南溪人, 博士研究生, 主要从事生物信息学和数据挖掘方向的研究
  • 1. 西南大学 经济管理学院, 重庆 400715
  • 2. 西南大学 数学与统计学院, 重庆 400715
  • 收稿日期:  2017-03-16
基金项目:  国家自然科学基金项目（20130695）

摘要: 多形性胶质母细胞瘤（GBM）是一种最常见且致死率极高的脑部肿瘤.为了解决传统生存模型不能处理变量p远大于样本数n的基因表达数据的缺点，本文构建了一个关键基因筛选算法——SSLC算法.该算法结合限制性优化算法和生存模型筛选出了与生存时间相关的GBM关键基因，并通过比较证明了此算法优于传统经典算法，最后通过文献查找证明筛选出的部分基因是已经证实的和GBM高度相关的基因，为GBM的靶向制药打下基础.

English Abstract

    全文HTML

  • 癌症是一大类疾病的总称，其共同点是失去控制的细胞增殖.在众多的癌症疾病中，多形性胶质母细胞瘤(GBM)是一种神经胶质瘤，是最常见且致死率极高的脑部肿瘤，这种脑瘤具有高侵润性，可大范围转移.同时，该肿瘤细胞对放疗不甚敏感，非常容易复发.据文献报道神经胶质瘤的中位生存时间和无进展生存时间分别为14.6个月和6.9个月，5年生存率为9.8% [1].由于癌症是基因水平上的遗传性疾病[2]，所以神经胶质瘤的发生应该是一个多因素作用、多基因参与、经过多个阶段才最终形成的极其复杂的生物学现象.因此，本文从基因层面研究该癌症的致病机制.

    从国内外研究来看，在关键基因筛选方面，文献[2]利用STRING工具筛选出一些GBM关键基因；文献[3]通过对GBM患者的基因表达数据进行分析，发现BITC是GBM治疗的潜在生物标志物；文献[4]利用距离加权算法筛选出了与卵巢癌相关的基因.然而，从当前国内外的相关研究来看，没有把关键基因的筛选和GBM患者的生存时间联系起来.由于临床上通常使用无进展生存时间(Progression-free survival)或总生存时间(Overall survival)来对肿瘤等疾病的疗效及预后予以考核，所以把生存时间作为筛选的因素之一.本文拟使用能处理生存时间的生存分析模型[5]来选取和GBM生存时间相关的关键基因，提高基因筛选的准确性.但是由于基因表达数据的高维低样本特点(p≫n)，传统的生存分析方法很难对其予以有效的分析，因此我们将以此问题作为起点，对GBM患者的关键基因筛选进行研究.

1.   GBM基因表达数据

  • 基因表达数据反映的是直接或间接测量得到的基因转录产物mRNA在细胞中的丰度(即反应细胞组织中特定的mRNA平均分子数)，可以用来分析基因之间的相关性，推理未知功能的基因，诊断患者的疾病状态，在理解肿瘤发病机制，识别致癌基因，诊断与预防癌症等方面有着重要的应用.

    基因表达数据的主要形式是矩阵形式，行表示基因，列表示实验样本[6].数据格式如下所示

    Xij表示基因i在不同的实验条件或不同细胞组织j下的表达值，经过数据标准化后，基因表达数据可以进行统计学和生物学分析.

2.   GBM关键基因筛选算法

  • 本文结合限制性优化算法和生存模型构建了一种新的GBM关键基因筛选算法(SSLC算法)，在介绍这种新算法之前，先介绍生存模型和几种限制性优化算法.

    • 2.1.   Cox风险比例模型

  • 在医学中，对病人治疗效果的考察，不仅要看疗效的好坏，还要看患者生存时间的长短.生存分析(Survival analysis)是肿瘤和其他慢性疾病疗效评价和预后分析的主要方法[7]. Cox比例风险模型是生存分析方法中最为流行的一种，Cox模型用风险函数来反映协变量对生存期的影响.现假定有n个观测，对每个观测i得到观测值(t，δi，Xi)，其中，t为生存时间；δi为截尾指示变量，如果观测i为截尾数据，δi=0，如果观测i为非截尾数据，δi=1；Xi=(xi1，xi2，xip)为p维行向量，表示观测i的第p个协变量. Cox比例风险系数的一般形式为

    式中，X=(x1，x2，…，xp)T表示p维协变量向量，β=(β1，β2，…，βp)表示回归系数向量，h0(t)为基准风险函数，则第i个个体的风险率为

    其中，X，β，h0(t)的含义同公式(1).

    • 2.2.   限制性优化算法

  • 经典的Cox风险比例模型擅于处理样本数(n)大于变量(p)的情况[8]，然而GBM基因表达数据的变量远大于样本数(p≫n).在我们使用的数据中，样本数为227，基因即变量为10 992.经典Cox风险比例模型不能处理p≫n的数据.因此，我们将能处理p≫n数据的限制性优化算法引入到经典的Cox风险比例模型中，用来处理低样本高变量的GBM基因数据.

    1) LASSO(The Least Absolute Shrinkage and Selectionator Operator)算法是限制性优化算法中使用较广泛的经典算法[8].该算法通过构造惩罚函数来获得一个精炼的模型，最终确定一些指标的系数为0. LASSO的公式为

    满足

    式中，xij表示预测变量，yi表示结果变量，β=(β0，β1，…，βp)表示回归系数向量，t为调整参数.

    随后Tibshirani提出了CoxLasso算法[8]，即把LASSO和Cox风险比例模型结合，用来处理变量p远大于样本数n且和生存时间相关的数据，可以用来处理癌症基因表达数据.

    满足

    这等价于以下优化问题：

    其中λ为控制稀疏性的调整参数. CoxLasso算法可由R程序中“glmnet”包中的glmnet方法实现.

    2) 稀疏主成分算法SPCA(sparse PCA)

    主成分分析(PCA)是一类有效的特征提取算法，能够进行特征提取和数据降维.但是，由于主成分分析最终给出的主成分是原来的数据变量的线性组合，因此无法解释每一个主成分对应的特征是什么.特别是把主成分分析应用到基因数据处理时，原始变量可能有成千上万个，那么每一个主成分都是成千上万个变量的线性组合，因此难以解释主成分的含义.

    稀疏主成分分析算法解决了这个问题[9].通过增加一个惩罚函数，它会把主成分系数变的稀疏[10]，把大多数系数都变成0，通过这样一种方式，就可以把主成分中最重要的部分保留下来，适用于基因数据处理，公式如下：

    最大化

    满足

    X为中心化样本矩阵，A为协方差矩阵，S是某正整数.

    • 2.3.   GBM关键基因筛选算法——SSLC算法

  • 1) 数据清洗

    本文使用的数据来源为Repository for Molecular Brain Neoplasia Data (REMBRANDT) (https://caintegrator.nci.nih.gov/rembrandt)提供的GBM基因表达数据(227个样本)，芯片型号为Affymetrix U133 plus 2.0，数据集如表 1所示.

    原始的GBM微阵列数据(CEL类型文件)由Bioconductor项目(http://www.bioconductor.org/)提供的R程序(“affy”包中的justRMA方法)进行归一化处理和预处理.经过预处理后，在数据矩阵中有227个样本和54 675个基因；然后，用“GeneFilter”包中的nsfilter方法来筛选出基因表达变化大的基因；最后，GBM的基因表达数据矩阵变为227个样本和10 992个基因.

    2) SSLC算法

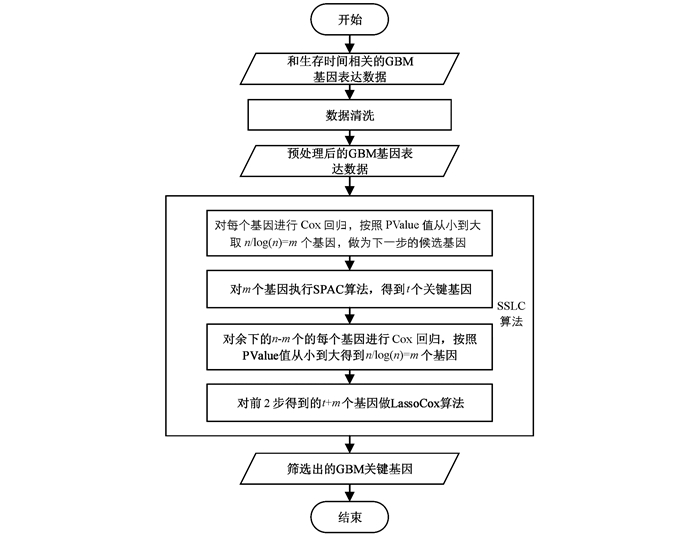
    Tibshirani的CoxLasso算法可以用来处理和生存时间相关的高维低样本的GBM基因表达数据，但由实验结果(表 2)可知，由于CoxLasso算法强制把某些参数设置为0，最后筛选出的基因为12个.在未被选中的基因中很可能还存在与GBM相关的基因，这就是假阴性问题.因此我们设计了SSLC算法，通过SIS+SPCA+CoxLasso算法的组合来得到更好的基因筛选结果.本算法由R程序实现.算法流程图如图 1所示，算法步骤如下：

    第一，对单个基因(n为样本数，本例n=10 992个)逐个做Cox回归，每个基因得到一个对应的PValue值，对其从小到大排序，然后按照PValue值从小到大取n/log(n)=m个基因(本例m=83)，作为下一步的候选基因；选取n/log(n)个基因是为了把p变成比n小，但又不能小太多.实现的关键函数为“glmnet”包中的coxph函数；

    第二，对这m个基因执行SPAC算法(稀疏主成分算法)，得到t个(本例t=30) 关键基因；实现的关键函数为“nsprcomp”包中的nsprcomp函数；

    第三，对余下的n-m(本例10 992-83=10 909) 个基因继续执行步骤一，仍然按照PValue值从小到大得到n/log(n)=m(本例m=83) 个基因；关键函数为“glmnet”包中的coxph函数；

    第四，对第二步和第三步得到的t+m(本例30+83=113) 个基因做CoxLasso算法，得到28个关键基因(表 2).关键函数为“glmnet”包中的cv.glmnet函数.

    结果如表 2所示：

    在SSLC算法(SIS+SPCA+LASSO+Cox算法)中引入了SPCA算法，并反复从候选基因中进行筛选(第一步和第二步，相当于SIS过程)，从某种程度上解决了传统的CoxLasso算法假阴性的问题，能为生物医学工作者提供更多的GBM候选关键基因.

    • 2.4.   SSLC算法和传统的CoxLasso算法的预测性能比较

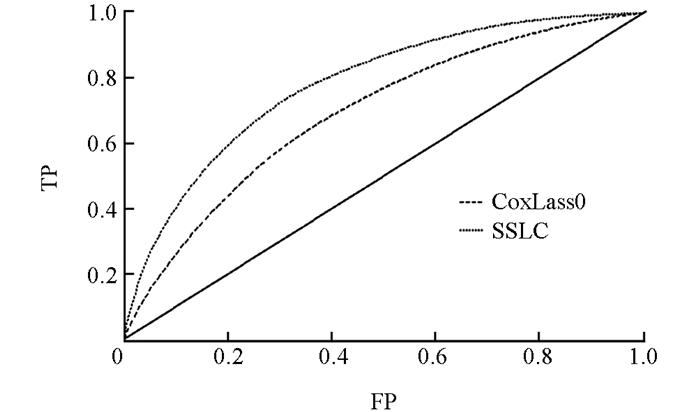
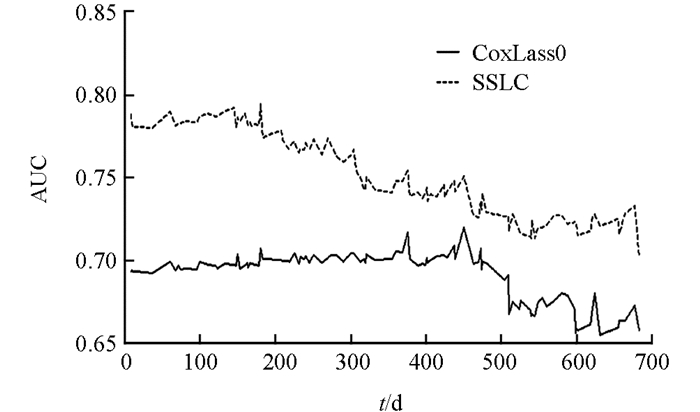
  • 我们利用受试者工作特征曲线ROC(receiver operating characteristic curve)及曲线下的面积AUC来量化2个算法对GBM生存时间预测的准确性[11].

    ROC曲线和AUC常被用来评价二值分类器的优劣.一般来说，在ROC曲线中最靠近坐标轴左上方的曲线所代表的分类器准确率最高，在AUC曲线中，曲线下面积越大，诊断准确性越高. ROC和AUC曲线可由R程序的“risksetROC”程序包实现.由图 2、图 3可知，SSLC算法的ROC曲线更靠近坐标轴左上方，AUC曲线下面积也更大，因此SSLC算法要优于传统的CoxLasso算法.

    • 2.5.   对SSLC算法筛选出的部分基因通过文献查找进行分析

  • 在筛选出的关键基因中，查找文献发现，EIF3A在一些癌症中是起正向调节作用的，而且已经发现在一些胶质瘤患者中EIF3A呈高表达[12]；IL17RC是一个关键的白细胞介素信号分子，它在GBM的发病过程中对免疫反应和炎症反应起着重要作用[13]；GDNF是一种胶质细胞源性神经营养因子，促进神经元存活[14]；AEBP1是转录阻遏因子，它在不同组织和器官中的表达水平不同，在脑组织细胞中表现的较强[15]，而且它可以与肿瘤抑制蛋白PTEN结合，并抑制其肿瘤抑制功能[16].众所周知，和AEBP1密切相关的PTEN和NF-κB，在GBM肿瘤的进展中起着非常重要的作用.

    由此可见，SSLC算法筛选出的基因中有很多是已经证实和GBM高度相关的，还有部分基因虽然现在还未见和GBM相关的文献报道，但可以以此基因为依据选出一些感兴趣的基因作为实验研究的对象.

3.   结束语

  • 现在国内外对GBM关键基因的筛选研究没有和生存时间联系起来，为了解决这个问题，本文把限制性优化算法引入到生存模型中，构建了一种新的GBM关键基因筛选算法(SSLC算法)，筛选出了与生存时间相关的GBM关键基因，并比较了SSLC算法与传统CoxLasso算法的区别.最后通过文献查找证明筛选出的部分基因是已经证实的和GBM高度相关的基因.进一步的研究将致力于以这些关键基因为基础，推导出GBM的关键蛋白质，为GBM的靶向制药打下基础.

参考文献 (16)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回