高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

高压下γ-Ca3N2晶体的结构，电子和光学性质的第一性原理研究

,  ,  , 

上一篇

下一篇

李佐, 廖大麟, 王朴, 等. 高压下γ-Ca3N2晶体的结构，电子和光学性质的第一性原理研究[J]. 西南大学学报（自然科学版）, 2018, 40(2): 78-84. doi: 10.13718/j.cnki.xdzk.2018.02.013
引用本文: 李佐, 廖大麟, 王朴, 等. 高压下γ-Ca3N2晶体的结构，电子和光学性质的第一性原理研究[J]. 西南大学学报（自然科学版）, 2018, 40(2): 78-84. doi: 10.13718/j.cnki.xdzk.2018.02.013
shu
Zuo LI, Da-lin LIAO, Pu WANG, et al. First Principles Study of the Structural, Electronic and Optical Properties of γ-Ca3N2 Crystal Under High Pressure[J]. Journal of Southwest University Natural Science Edition, 2018, 40(2): 78-84. doi: 10.13718/j.cnki.xdzk.2018.02.013
Citation: Zuo LI, Da-lin LIAO, Pu WANG, et al. First Principles Study of the Structural, Electronic and Optical Properties of γ-Ca3N2 Crystal Under High Pressure[J]. Journal of Southwest University Natural Science Edition, 2018, 40(2): 78-84. doi: 10.13718/j.cnki.xdzk.2018.02.013
shu

高压下γ-Ca3N2晶体的结构，电子和光学性质的第一性原理研究

  • 1.

    贵州工程应用技术学院 理学院，贵州 毕节 551700

  • 2.

    聊城大学 物理科学与信息技术学院，山东 聊城 252000

  • 基金项目: 国家自然科学基金项目(11504153);贵州省科技厅联合基金项目(黔科合LH[2014]7525);贵州工程应用技术学院自然科学基金项目(20112025)
详细信息
    作者简介:

    李佐(1983-)，男，陕西宝鸡人，讲师，主要从事高压下材料物性研究 .

  • 中图分类号: O521+.21

First Principles Study of the Structural, Electronic and Optical Properties of γ-Ca3N2 Crystal Under High Pressure

  • 1.

    School of Science, Guizhou University of Engineering Science, Bijie Guizhou 551700, China

  • 2.

    School of Physical Science and Information Technology, Liaocheng University, Liaocheng Shandong 252000, China

  • 摘要: 采用广义梯度近似(GGA)框架下平面波超软赝势第一性原理方法，研究了γ-Ca3N2晶体在0~115 GPa高压下的结构、电子和光学性质.晶体中两种不同类型的Ca—N键长随压强的变化表明八面体的Ca—N键长比十二面体的键长有轻微的压缩.随着压强增大，价带向高能区移动，而导带向低能扩展，晶体的带隙变窄.基于Mulliken布局分析，γ-Ca3N2晶体随着压强增大，共价性增强.同时，在高压下晶体的吸收光谱显示出红移的趋势.
    Abstract: A plane wave ultrasoft pseudopotential implementation of first principles in the framework of the generalized gradient approximation (GGA) is utilized to calculate the structural, electronic and optical properties of the γ-Ca3N2 crystal under a hydrostatic pressure of 0-115 GPa. The change of bond lengths of two different types of Ca—N bond with pressure demonstrates that the octahedral Ca—N bond is slightly compressible compared to the dodecahedral Ca—N. As the pressure increases, the valence band moves toward the high energy region, while the conduction band extends toward the low energy region, and the band gap of the crystal becomes narrower. Based on the Mulliken population analysis, the crystal displays a much higher covalent character with increasing pressure. In addition, the absorption spectra of γ-Ca3N2 crystal show a trend of red shift under high pressure.
  • 加载中

  • 图 1  高压相γ-Ca3N2晶体结构图

    下载: 全尺寸图片 幻灯片

    图 2  Ca—N键长随压强的变化关系

    下载: 全尺寸图片 幻灯片

    图 3  γ-Ca3N2晶胞体积和压强的变化关系

    下载: 全尺寸图片 幻灯片

    图 4  弹性系数随压强的变化关系

    下载: 全尺寸图片 幻灯片

    图 5  零压下γ-Ca3N2晶体的态密度

    下载: 全尺寸图片 幻灯片

    图 6  在10 GPa和80 GPa下γ-Ca3N2晶体的态密度分布

    下载: 全尺寸图片 幻灯片

    图 7  在10 GPa和80 GPa下γ-Ca3N2晶体的能带结构

    下载: 全尺寸图片 幻灯片

    图 8  γ-Ca3N2晶体带隙随压强的变化关系

    下载: 全尺寸图片 幻灯片

    图 9  γ-Ca3N2晶体化学键布局分布随压强的变化关系

    下载: 全尺寸图片 幻灯片

    图 10  不同压强下γ-Ca3N2晶体的吸收系数

    下载: 全尺寸图片 幻灯片

    表 1  γ-Ca3N2晶体理论和实验原子坐标

    原子 Wyckoff坐标 GGA-PBE 实验[7]
    Ca 16c (0.049 90，0.049 90，0.049 90) (0.047 62，0.047 62，0.047 62)
    N 12a (3/8，0，1/4) (3/8，0，1/4)
    下载: 导出CSV

    表 2  零压下γ-Ca3N2晶体理论和实验数据

    空间群 a/nm b/nm c/nm V/nm3 N—Ca键长/nm(十二面体中) N—Ca键长/nm(八面体中) B0/GPa
    本文工作 I-43D 0.765 8 0.449 2 0.239 8 0.294 9 64.77
    实验值[7] I-43D 0.772 1 0.460 3 0.240 3 0.299 4
    其他理论值[6] Pbcn 0.620 3 0.635 2 0.895 9 0.353 0 73
    下载: 导出CSV

    表 3  不同压强下的离子组态

    压强/GPa 离子组态
    0 Ca+0.83N-1.11
    15 Ca+0.80N-1.07
    25 Ca+0.78N-1.05
    40 Ca+0.76N-1.02
    60 Ca+0.74N-0.99
    80 Ca+0.72N-0.96
    100 Ca+0.70N-0.93
    10 Ca+0.81N-1.08
    20 Ca+0.79N-1.06
    30 Ca+0.78N-1.04
    50 Ca+0.75N-1.00
    70 Ca+0.73N-0.97
    90 Ca+0.71N-0.95
    110 Ca+0.69N-0.92
    下载: 导出CSV
  • [1] 肖芬, 娄姗姗, 胡发波, 等.高压下硅烷的第一性原理研究[J].西南大学学报(自然科学版), 2016, 38(9): 153-158. doi: http://xbgjxt.swu.edu.cn/jsuns/jsuns/ch/reader/view_abstract.aspx?file_no=201609024&flag=1
    [2] 刘祥林. GaN基材料的生长及蓝光LED的研制[D]. 北京: 中国科学院半导体研究所, 1998.
    [3] RÖMER S R, SCHNICK W, KROLL P. Density Functional Study of Calcium Nitride: Refined Geometries and Prediction of High-Pressure Phases[J]. J Phys Chem C, 2009, 113(7): 2943-2949. doi: 10.1021/jp8077002
    [4] RÖMER S R, DÖRFLER T, KROLL P, et al. Group Ⅱ Element Nitrides M3N2 Under Pressure: A Comparative Density Functional Study[J]. Phys Stat Solidi B, 2009, 246(7): 1604-1613. doi: 10.1002/pssb.v246:7
    [5] HAO Jian, LI Yin-wei, ZHOU Qiang, et al. Structural Phase Transformations of Mg3N2 at High Pressure: Experimental and Theoretical Studies[J]. Inorg Chem, 2009, 48(20): 9737-9741. doi: 10.1021/ic901324n
    [6] HAO Jian, LI Yin-wei, Wang Jin-shen, et al. Experimental Determinations of the High-Pressure Crystal Structures of Ca3N2[J]. J Phys Chem C, 2010, 114(39): 16750-16755. doi: 10.1021/jp105861y
    [7] BRAUN C, BÖRGER S L, BOYKO T D, et al. Ca3N2 and Mg3N2: Unpredicted High-Pressure Behavior of Binary Nitrides[J]. J Am Chem Soc, 2011, 133(12): 4307-4315. doi: 10.1021/ja106459e
    [8] LI Shu-xing, LIU Xue-jian, MAO Rui-hua, et al. Red-Emission Enhancement of the CaAlSiN3: Eu2+ Phosphor by Partial Substitution for Ca3N2 by CaCO3 and Excess Calcium Source Addition[J]. RSC Adv, 2015, 93(5): 76507-76515.
    [9] PERDEW J P, BURKE K, ERNZERHOF M. Generalized Gradient Approximation Made Simple[J]. Phys Rev Let, 1996, 77(18): 3865-3868. doi: 10.1103/PhysRevLett.77.3865
    [10] VANDERBILT D. Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism[J]. Phys Rev B, 1990, 41(11): 7892-7895. doi: 10.1103/PhysRevB.41.7892
    [11] FISCHER T H, ALMLOF J. General Methods for Geometry and Wave Function Optimization[J]. J Phys Chem, 1992, 96(24): 9768-9774. doi: 10.1021/j100203a036
    [12] MILMAN V, WINKLER B, WHITE J A, et al. Electronic Structure, Properties, and Phase Stability of Inorganic Crystals: A Pseudopotential Plane-Wave Study[J]. Inter J Quan Chem, 2000, 77(5): 895-910. doi: 10.1002/(ISSN)1097-461X
    [13] CHADI D J. Special Points for Brillouin-Zone Integrations[J]. Phys Rev B, 1977, 16(4): 1746-1750. doi: 10.1103/PhysRevB.16.1746
    [14] MULLIKEN R S. Electronic Population Analysis on LCAO-MO Molecular Wave Functions. I[J]. J Chem Phys, 1955, 23(10): 1833-1840. doi: 10.1063/1.1740588
    [15] 马天慧. LiNbO3光学性质与热力学性质的第一性原理计算[J].西南师范大学学报(自然科学版), 2014, 39(5): 22-26. doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xnsfdxxb201405005
    [16] BOCQUET A E, MIZOKAWA T, MORIKAWA K, et al. Electronic Structure of Early 3d-Transition-Metal Oxides by Analysis of the 2p Core-Level Photoemission Spectra[J]. Phys Rev B, 1996, 53(3): 1161-1170. doi: 10.1103/PhysRevB.53.1161
    [17] CHING Wai-yim. Theoretical Studies of the Electronic Properties of Ceramic Materials[J]. J Am Cera Soc, 1990, 73(11): 3135-3160. doi: 10.1111/jace.1990.73.issue-11
    [18] SAHA S, SINHA T P, MOOKERJEE A. Structural and Optical Properties of Paraelectric SrTiO3[J]. J Phys: Condensed Matter, 2000, 12(14): 3325-3336. doi: 10.1088/0953-8984/12/14/309
  • 加载中
图( 10) 表( 3)
计量
  • 文章访问数:  1215
  • HTML全文浏览数:  628
  • PDF下载数:  191
  • 施引文献:  0
出版历程
  • 收稿日期:  2017-03-23
  • 刊出日期:  2018-02-20

高压下γ-Ca3N2晶体的结构，电子和光学性质的第一性原理研究

    作者简介: 李佐(1983-)，男，陕西宝鸡人，讲师，主要从事高压下材料物性研究
  • 1. 贵州工程应用技术学院 理学院，贵州 毕节 551700
  • 2. 聊城大学 物理科学与信息技术学院，山东 聊城 252000
  • 收稿日期:  2017-03-23
基金项目:  国家自然科学基金项目(11504153);贵州省科技厅联合基金项目(黔科合LH[2014]7525);贵州工程应用技术学院自然科学基金项目(20112025)

摘要: 采用广义梯度近似(GGA)框架下平面波超软赝势第一性原理方法，研究了γ-Ca3N2晶体在0~115 GPa高压下的结构、电子和光学性质.晶体中两种不同类型的Ca—N键长随压强的变化表明八面体的Ca—N键长比十二面体的键长有轻微的压缩.随着压强增大，价带向高能区移动，而导带向低能扩展，晶体的带隙变窄.基于Mulliken布局分析，γ-Ca3N2晶体随着压强增大，共价性增强.同时，在高压下晶体的吸收光谱显示出红移的趋势.

English Abstract

    全文HTML

  • 静高压作为一种极端条件，为材料研究提供了一种重要的途径[1].氮化金属材料的研究比较重要，著名的GaN半导体材料是蓝光LED的主要发光材料[2].高压下第二主族元素氮化物M3N2(M=Be，Mg，Ca，Sr，Ba)的性质研究是一个重要的研究领域. 2009年RÖMER等人[3-4]理论预测了几种未知的高压相Ca3N2和Mg3N2.随后吉林大学郝健等人[5-6]从实验和理论方面研究了两种氮化物的高压性质，理论研究结果与RÖMER的结果是一致的.文献[5-6]中γ相的Ca3N2没有被XRD实验观测到，但是，2011年德国科学家BRAUN等人[7]在实验中合成了新的高压相γ-Ca3N2.近年来，人们对Ca3N2的研究主要集中在用其作为发光薄膜材料上[8]，而并未对γ-Ca3N2晶体有深入的研究.本文基于第一性原理方法，研究了新的高压相γ-Ca3N2.主要计算了材料在常压下的晶体结构，预测了高压下的电子结构和光学性质，为进一步的研究提供参考.

1.   计算方法和模型

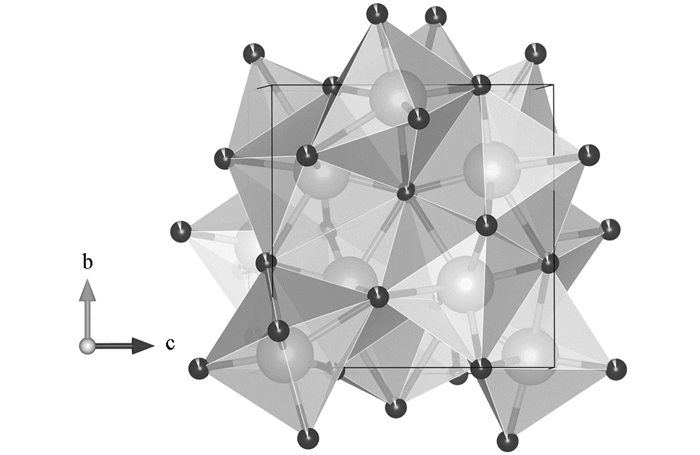
  • 对高压相γ-Ca3N2晶体在0~115 GPa压力区间的性质进行了计算.计算过程均采用周期性边界条件，电子间的交换关联函数采用广义梯度近似(GGA)的PBE [9](Perdew-Burke-Ernzerhof)方法; 晶体中电子的波函数由平面波基组展开，并由超软赝势实现离子实与价电子之间的相互作用势[10]; 结构弛豫使用BFGS算法[11]，所有的计算都是在CASTEP软件包中完成[12].平面波截断能设置为470 eV，氮原子的2s22p3和钙原子的3s23p64s2轨道电子波函数被使用.布里渊区采用Monkhorst-Pack框架下的9×9×9 k点方案[13].这些设置可以使总能量的收敛标准达到0.01%以内.在几何优化中，体系总能量收敛标准小于每原子1.0 × 10-6 eV，作用力小于0.02 eV/nm.采用实验结构(a=b=c=0.772 1 nm)作为理论计算的初始构型[7].晶体结构中包含两种Ca—N键类型，氮原子处于6个钙原子构成的八面体中，而钙原子处于8个氮原子构成的十二面体中(图 1).理论计算晶体坐标和实验结果比较(表 1)，计算结果和实验符合得很好，表明计算是精确的、可靠的.

2.   结果与讨论

    2.1.   几何结构和弹性特征

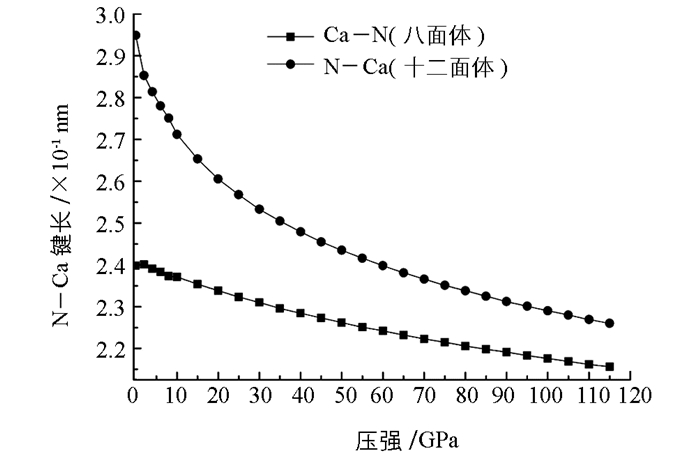
  • 采用GGA交换关联势的BFGS方法研究了不同压强下γ-Ca3N2晶体的性质.为了确认晶体的稳定性和计算精度，表 2中给出了零压强下晶体的晶格参量、晶胞体积、键长和弹性模量，并与实验数据和其他理论结果进行比较.从表 2中可以发现，本文计算的晶格常数a与实验值的相对误差只有0.8%，晶胞体积误差为2.4%，十二面体中氮原子与钙原子之间的键长理论值与实验值的误差为2%，而八面体中误差只有1.5%.实验值中未给出γ-Ca3N2晶体的弹性模量，但是与其他理论计算的类似结构的弹性模量相近.这些结果进一步表明本文计算结果是可靠的. γ-Ca3N2晶体结构中两种不同类型的Ca—N化学键. 图 2给出了在不同压强作用下，这两种键长的变化情况.可以发现，在高的压强作用下，键长都被压缩了.同时，随着压强的增大，两种Ca—N键长之间的差别越来越小.十二面体中的Ca—N键长在0~50 GPa的压强范围内，变化相对比较陡峭，当压强增加到115 GPa时，键长减小了23%.而八面体中的Ca—N键长在压强作用下变化的比较缓慢，键长减小了10%.因此，这些结果表明八面体中的Ca—N键长比十二面体中的Ca—N键长有较小的压缩率.

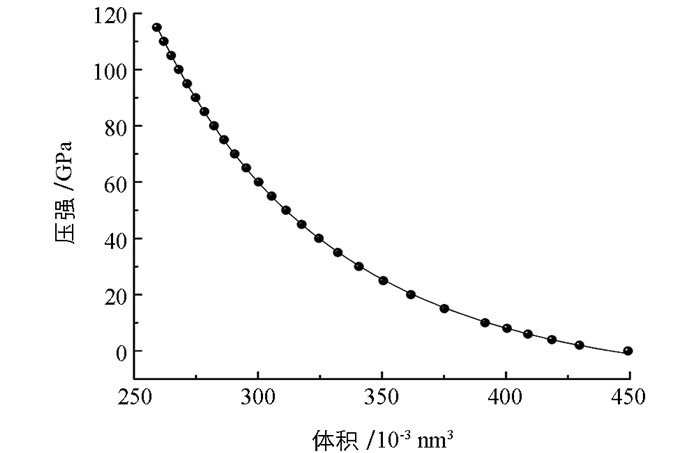
    体弹模量B0作为表征材料硬度的一个参量，可以通过物态方程拟合获得.利用(1)式Birch-Murnaghan关系拟合压强-体积曲线(图 3). (1)式中x等于V/V0，拟合B0时，设定B′0等于4.43. 表 2中的体弹模量数值即为拟合结果.

    对于立方晶体的力学稳定性判据，弹性系数Cij满足

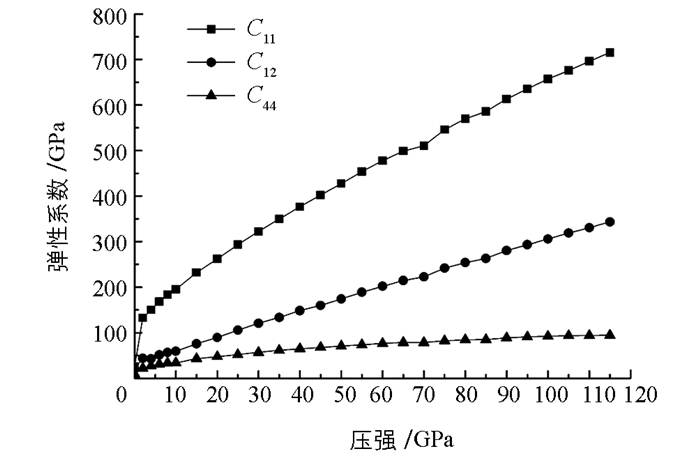
    图 4给出了弹性系数Cij随压强的变化关系.从图 4中可以发现，在0~115 GPa的压强范围内，始终满足稳定性判据.同时，随着压强的增加，弹性系数也在增大.因此，对于立方结构的γ-Ca3N2晶体无论在低压下还是高压下都保持了力学稳定性.

    • 2.2.   电子结构和电荷分布

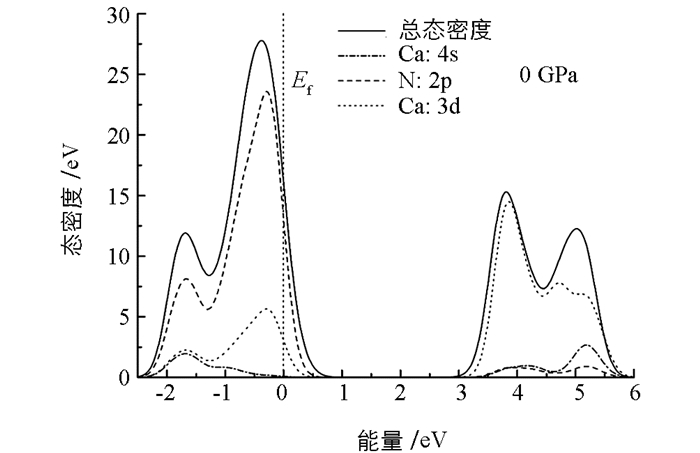
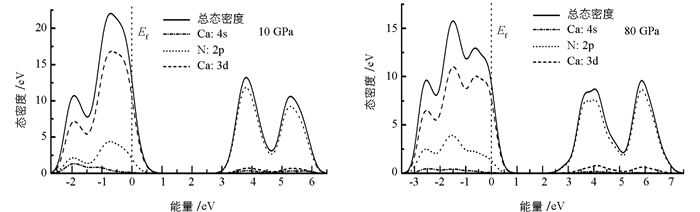
  • 为了理解γ-Ca3N2晶体态密度(DOS)随压强的变化关系，首先分析了零压下的态密度(图 5).对于γ-Ca3N2晶体，零压下存在一个2.873 eV的宽直接带隙(导带底最低点和价带顶最高点之间的能量差值).费米能级被设置在能量为零的位置.在价带的上部，氮原子的2p电子对态密度贡献较多，2s轨道电子则较少.钙原子的电子结构比较特别，其3d空轨道也会影响自身的能带结构.非占有的钙原子3d态和4s电子都对价带有贡献，分别在-0.273和-1.715 eV能量位置出现两个峰.在能带结构中，导带也比较强.也可以发现由非占有的钙原子3d态和4s电子贡献的导带区域.同时，零压下N-2p和Ca-4s态密度在3.496 eV和4.735 eV能量附近存在轨道杂化.

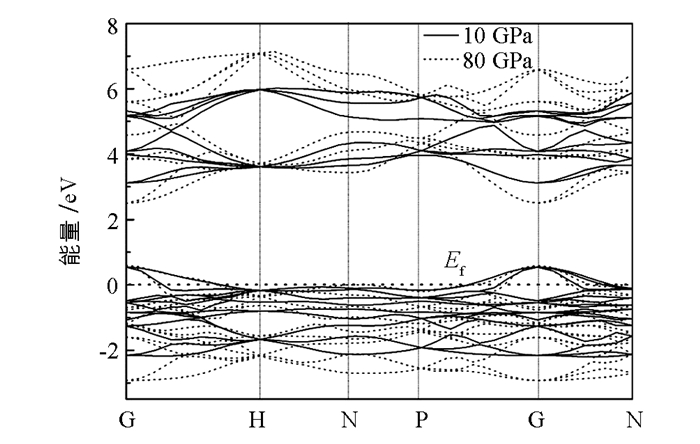
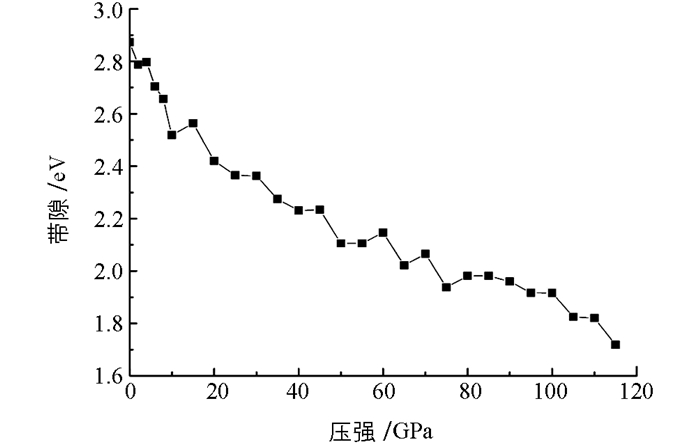
    进一步研究高压下的态密度分布，使用主自旋态之和，分别计算了钙原子s，d轨道和氮原子的p轨道的态密度分布(图 6).比较图 5和图 6可以发现，随着压强的增大，态密度分布强度减小，导带底向低能区域移动.在80 GPa的压强下，价带峰发生了分裂，同时，N-2p和Ca-4s态的杂化程度，随压强增大而减小，说明化学键级也被改变. 图 7给出了10 GPa和80 GPa下的能带结构，从图 7中可以发现带隙变化比较明显，结果和图 6是一致的. 图 8为带隙随压强的变化关系，在高压下，材料的带隙明显减小.从图 5-7中，也可以看出，费米能级进入到价带，表明γ-Ca3N2晶体材料为p型半导体材料.

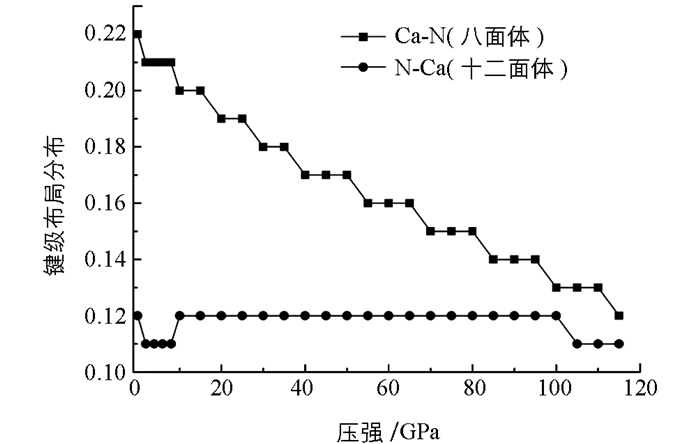
    Mulliken布局分析常被用来讨论材料化学键的共价性和离子性[14].利用Mulliken方法计算了共价轨道的轨道占据和电荷分布. γ-Ca3N2晶体在不同压强下的离子组态见表 3.零压下的离子组态为Ca+0.83N-1.11，这里的“+”和“-”号分别代表失去和得到电荷.随着压强的增大，钙原子和氮原子之间有较小的电荷迁移.同时得到了不同压强下N—Ca键的键级布局分布(图 9).从图 9中可以发现，八面体和十二面体中的N—Ca键布局分布的变化有着显著的不同.八面体中的N—Ca键的变化陡峭，而十二面体中的N—Ca键的变化平缓.当压强增加时，这种键级布局分布的差别逐渐减小.这些结果说明γ-Ca3N2晶体中键的共价性随着压强增大而增强.需要指出的是Mulliken分析数值与原子轨道线性组合基组的选取有关，分析成键具有局限性，但是对电荷的变化趋势分析是可靠的.

    • 2.3.   光学性质

  • 知道电子波函数和能量，就可以计算出介电常数[15]ε(ω)=ε1(ω)+iε2(ω)，介电常数的虚部ε2(ω)可以采用Kubo-Greenwood公式[16]从直接内部带迁移中获得.

    其中，ħω为声子能量，Ω为晶胞体积，ψkn(r)和ψkl(r)分别为始末态波函数，fki和εki分别表示ith态的费米配分函数和电子能量.介电常数的实部ε1(ω)，可以通过Kramers-Kronig(KK)关系获得[17]：

    其中M表示积分的初始值.可以得出吸收系数α(ω)的表达式[18]为

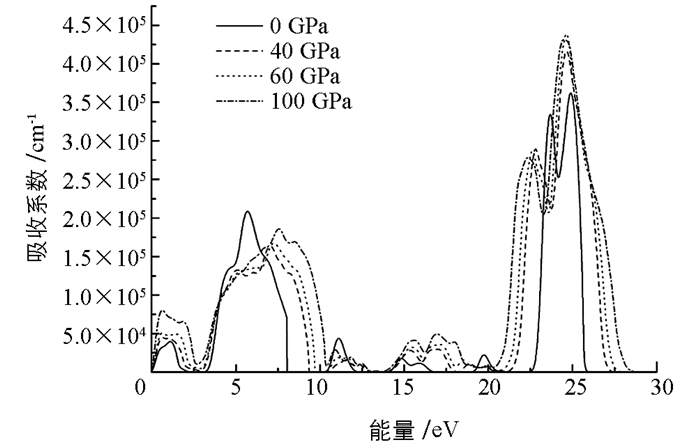
    图 10给出了不同压强下γ-Ca3N2晶体的吸收系数.吸收光谱的性质决定于γ-Ca3N2晶体的结构，因为γ-Ca3N2晶体是各向同性的，所以光谱也表现出各向同性.计算所得光谱只包含直接内带跃迁.零压下光谱中主要有7个吸收峰，分别属于近红外光谱区、可见光谱区和紫外光谱区.高压下吸收光谱主要集中在紫外光谱区.随着压强的增大，紫外光谱区有向低能区移动的趋势.由于在压力的作用下，价带向高能区移动，而导带向低能区都扩展，致使电子跃迁需要吸收的能量减小，所以光谱有向低能(红移)方向移动的趋势.光谱带隙逐渐变窄，这一结果和直接带隙的变化趋势是一致的.这些结果表明Ca3N2晶体有可能作为高压下的光谱器件材料.

3.   结论

  • 基于密度泛函理论的第一性平面波赝势方法，研究了0~115 GPa高压下立方Ca3N2晶体的几何结构，电子结构和光学性质.常压下的晶体结构参数很好的符合了实验结果.晶体中两种不同类型的Ca—N键长随压强的变化，说明八面体中的Ca—N键比十二面体中的Ca—N键有较小的压缩率.立方Ca3N2晶体拥有2.873 eV的宽带隙，随着压强的增大，带隙减小.基于Mulliken布局分析，发现随着压强的增加，Ca3N2晶体表现出较高的共价性.同时，吸收光谱在高的压力下表现出红移的趋势.本文的研究为更好地理解高压下Ca3N2晶体性质提供了参考.

参考文献 (18)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回