定理1 系统(1)的正不变集为：

证  对任意(M，N，Z)∈Γ，有：

从而知解是非负的.由系统(1)的第一个方程可知：

由比较原理可得：${M \le \frac{{{k_1}r}}{{4{c_1}}}}$.将系统(1)的第二和第三个方程相加得：

其中

由比较原理可得：

所以，Γ是系统(1)的正不变集.

为了计算方便，现通过无量纲化变换：

得到相应的无量纲化系统：

定义

通过简单计算容易得到下列结果.

定理2 (i)系统(2)总存在一个灭绝平衡点E=(0，0，0)；

(ⅱ)当r₁＞μ₁时，系统(2)存在一个无免疫平衡点${\mathit{\boldsymbol{E}}_0} = \left( {\frac{{{r_1} - {\mu _1}}}{{{r_1}}},{\rm{ }}0,{\rm{ }}0} \right)$；

(ⅲ)当η₁-μ₂η₂＞0，r₂-r₂z^*-μ₃＞0时，系统(2)存在无肿瘤平衡点E₁=(0，y^*，z^*)；

(ⅳ)当r₁-y^*-μ₁＞0，r₂-r₂z^*-μ₃＞0，η₁-μ₂η₂＞0时，系统(2)存在唯一的共存平衡点E^*(x^*，y^*，z^*).

为了研究相关平衡点的局部稳定性，计算可得系统(2)在平衡点处的Jacobian矩阵为：

定理3 当r₁＜μ₁且r₂＜μ₃时，系统(2)的灭绝平衡点E是局部渐近稳定的.

证  系统(2)在E处的特征方程为

方程(3)显然存在特征根λ₁=r₁-μ₁，λ₂=-μ₂＜0，λ₃=r₂-μ₃.故当r₁＜μ₁且r₂＜μ₃时，E局部渐近稳定.定理得证.

定理4 假设r₁＞μ₁.当r₂＜μ₃时，系统(2)的无免疫平衡点E₀是局部渐近稳定的.

证  系统(2)在E₀处的特征方程为

方程(4)显然存在特征根λ₁=μ₁-r₁＜0，λ₂=-μ₂＜0，而λ₃=r₂-μ₃，故当r₂＜μ₃时，E₀稳定.定理得证.

定理5 假设

当

且

时，无肿瘤平衡点E₁局部渐近稳定.

证  系统(2)在E₁处的特征方程为：

方程(5)显然存在特征根λ₁=r₁-y^*-μ₁.另外两个特征根由下列方程决定：

注意到

故当

时，方程(6)的根均具有负实部.所以当

且

时，无肿瘤平衡点E₁局部渐近稳定.定理得证.

定理6 假设

当

时，共存平衡点E^*局部渐近稳定.

证  系统(2)在E^*处的特征方程为：

方程(7)显然存在特征根λ₁=-r₁x^*＜0.另外两个特征根由方程(6)决定.所以当

时，共存平衡点E^*局部渐近稳定.定理得证.

定义关于η₂的连续可微函数$\psi :[0,\infty ) \to \mathbb{R}$

令ψ(η₂)=0，并代入下式

可得

令$\eta _2^*$为方程(8)一个正根.定义：

可得如下定理7.

定理7 假设

当

时，系统(2)在η₂=$\eta _2^*$处发生Hopf分支.

证  当η₂=$\eta _2^*$时，根据

定理(6)中特征方程(7)可以写为：

易得此特征方程有一对纯虚根${\lambda _1} = \overline {{\lambda _2}} = {\rm i}\sqrt {\frac{{{\eta _1}{\eta _3}{y^*}{z^*}}}{{{{(1 + {\eta _2}{z^*})}^3}}}} $和一个负实根λ₃=-r₁x^*.

根据文献[7]，下面只需验证在$\eta _2^*$处发生Hopf分支的横截条件成立.令λ(η₂)=χ(η₂)+iν(η₂)，代入(7)式，并对η₂求导可得：

其中：

由上述方程可得：

其中：

若

则横截条件

成立，定理得证.

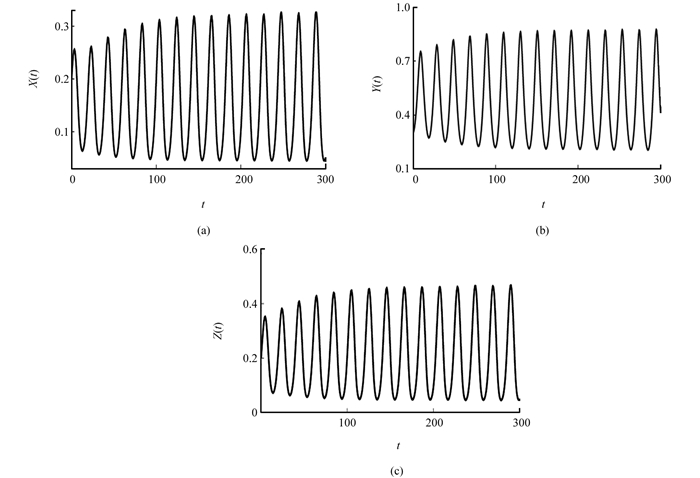
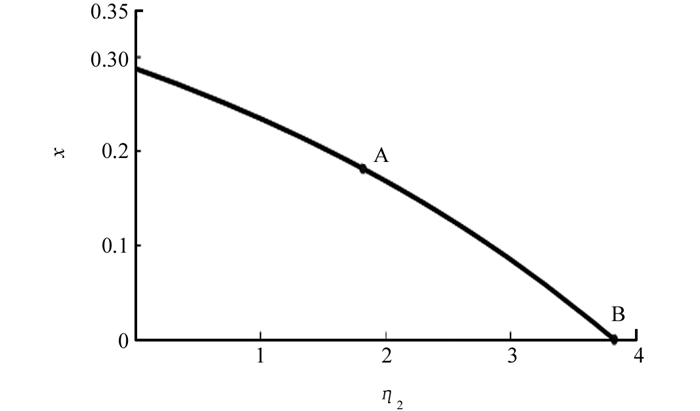
本节通过数值模拟验证上述理论研究结果.若取定参数r₁=0.8，μ₁=0.2，η₁=2.4，μ₂=0.3，r₂=0.79，η₃=1.6，μ₃=0.1，计算可得一元二次方程(8)存在两个正根，$\eta _2^*$=1.818 6或5.036 4.由Matcont分支软件可得系统(2)以η₂为分支参数的分支图(图 1)，其中A是Hopf分支点，B是分叉点，可以看到系统(2)会在$\eta _2^*$=1.818 6处发生Hopf分支.若取定η₂=2.5，直接计算得到此时平衡点x^*=0.129 1，y^*=0.496 7，z^*=0.181 8.此时系统(2)的时间序列图如图 2所示，系统处产生周期解，各变量产生周期振荡.

在已有研究中，静息态向狩猎态免疫细胞的转化以线性形式进行.本文理论分析及数值模拟发现，当静息态细胞以饱和形式转化，即与其相关的η₂超过阈值时，系统会通过Hopf分支产生周期解.这就表明静息态免疫细胞的转化形式对肿瘤动力学形态有重要影响.