高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

改进的超限学习机及其在不平衡数据中的应用

,  , 

上一篇

下一篇

李晗缦, 王丽丹, 段书凯. 改进的超限学习机及其在不平衡数据中的应用[J]. 西南大学学报（自然科学版）, 2020, 42(6): 140-148. doi: 10.13718/j.cnki.xdzk.2020.06.016
引用本文: 李晗缦, 王丽丹, 段书凯. 改进的超限学习机及其在不平衡数据中的应用[J]. 西南大学学报（自然科学版）, 2020, 42(6): 140-148. doi: 10.13718/j.cnki.xdzk.2020.06.016
shu
Han-man LI, Li-dan WANG, Shu-kai DUAN. An Improved Extreme Learning Machine and Its Application in Imbalanced Data[J]. Journal of Southwest University Natural Science Edition, 2020, 42(6): 140-148. doi: 10.13718/j.cnki.xdzk.2020.06.016
Citation: Han-man LI, Li-dan WANG, Shu-kai DUAN. An Improved Extreme Learning Machine and Its Application in Imbalanced Data[J]. Journal of Southwest University Natural Science Edition, 2020, 42(6): 140-148. doi: 10.13718/j.cnki.xdzk.2020.06.016
shu

改进的超限学习机及其在不平衡数据中的应用

  • 1.

    西南大学 电子与信息工程学院, 重庆 400715

  • 2.

    智能传动与控制技术国家与地方联合工程实验室, 重庆 400715

  • 3.

    智能计算与智能控制重庆市重点实验室, 重庆 400715

  • 基金项目: 国家自然科学基金项目（61571372，61672436）；中央高校基本科研业务费专项资金项目（XDJK2016A001，XDJK2017A005）
详细信息
    作者简介:

    李晗缦(1995-), 女, 硕士研究生, 主要从事神经网络和机器学习等方面的研究 .

    通讯作者: 王丽丹, 教授, 博士研究生导师; 

  • 中图分类号: TP183

An Improved Extreme Learning Machine and Its Application in Imbalanced Data

  • 1.

    School of Electronic and Information Engineering, Southwest University, Chongqing 400715, China

  • 2.

    National & Local Joint Engineering Laboratory of Intelligent Transmission and Control Technology, Chongqing 400715, China

  • 3.

    Brain-Inspired Computing & Intelligent Control of Chongqing Key Lab, Chongqing 400715, China

  • 摘要: 超限学习机（ELM）作为一种简单高效的学习算法被广泛应用于分类和拟合问题中.但是ELM在训练过程中逼近所有的样本容易造成过拟合，并且单个的ELM在不平衡数据分类上效果欠佳.因此，本文提出了一种新的基于分层交叉验证的集成超限学习机，该算法在训练阶段将集成学习和分层交叉验证相结合：①集成学习通过将若干个网络组合大大提高分类性能；②分层交叉验证最大程度学习样本的分布特点.基于KEEL数据库的不平衡数据分类问题的实验表明，新提出的算法更加稳定并且有更高的分类性能.
    Abstract: The extreme learning machine (ELM) has been widely applied in classification and regression learning due to its simple structure and fast learning capability. However, it might suffer from over-fitting as the network needs to approximate all samples, and single ELM is mediocre in imbalanced data classification. To deal with these problems, a novel ensemble extreme learning machine based on stratified cross-validation is proposed in this paper. Ensemble learning and stratified cross-validation are embedded into the training phase: ① ensemble learning greatly improves classification performance by combining several basic networks; ② stratified cross-validation could learn samples' distribution characteristics to the greatest extent. Experimental results of imbalanced data sets show that the proposed method is robust and more efficient for imbalanced classification.
  • 加载中

  • 图 1  K折交叉验证与分层交叉验证示意图

    下载: 全尺寸图片 幻灯片

    图 2  3种算法分类结果散点图

    下载: 全尺寸图片 幻灯片

    图 3  两种叶子照片

    下载: 全尺寸图片 幻灯片

    表 算法1  基于分层交叉验证的集成超限学习机

    输入：训练集{(xj，tj)|xj∈Rn，tj∈Rm，j=1，2，…，N}；基础分类器个数L；隐层节点数Ñ；交叉验证倍数K；样本类别R.
    *****划分训练样本及初始化******
        1)随机产生wi和bi，i=1，2，…，Ñ.
        2)将每类样本分为K个子集，共R×K个子集.将R类样本的每个子集相加得到新的K个子集. (K-1)N/K的样本作为训练集，N/K的样本作为而测试集.
        3)将wi和bi的值赋给$\mathop {{w_i}}\limits^ \wedge$和$\mathop {{b_i}}\limits^ \wedge$.将G-mean的值保存在$G - \mathop m\limits^ \wedge ean$.
    *****权重优化阶段*****
    for l=1，2，…，L
        随机产生wil和bil，i=1，2，…，Ñ.
            for k=1，2，…，K
        计算第k个验证集的G-meankl.
            end for
            计算K个子集结果的平均值，也就是$G - mea{n^l} = (1/K)\sum\limits_{k = 1}^K G - mean_k^l$.
            if G-meanl > $G - \mathop m\limits^ \wedge ean$
        更新$\mathop {{w_i}}\limits^ \wedge$=wil，$\mathop {{b_i}}\limits^ \wedge$=bil.
            end if
        end for
    *****测试阶段****
    用$\mathop {{w_i}}\limits^ \wedge$和$\mathop {{b_i}}\limits^ \wedge$计算测试集的G-mean.
    输出：测试样本分类.
    下载: 导出CSV

    表 1  混淆矩阵

    目标为正类(T) 目标为负类(F)
    预测为正类(P) TP FP
    预测为负类(N) FN TN
    下载: 导出CSV

    表 2  数据集及参数

    数据集 样本数量 特征参数 不平衡率
    glass1 214 9 1.82
    haberman 306 3 2.78
    ecoli1 336 7 3.36
    new-thyroid1 215 5 5.14
    glass6 214 9 6.38
    ecoli3 336 7 8.6
    yeast-0-5-6-7-9_vs_4 528 8 9.35
    glass-0-1-6_vs_2 192 9 10.29
    yeast-1_vs_7 459 7 14.3
    page-blocks-1-3_vs_4 472 10 15.86
    glass5 214 9 22.78
    yeast5 1484 8 30.73
    下载: 导出CSV

    表 3  3种算法的结果比较

    数据集 隐层节点数Ñ G-mean/%
    ELM K折交叉验证的EN-ELM 基于分层交叉验证的EN-ELM
    glass1 50 72.95 73.44 75.33
    haberman 50 62.74 60.58 62.50
    ecoli1 50 89.75 89.57 91.46
    new-thyroid1 50 97.10 96.62 98.16
    glass6 50 95.17 95.63 95.43
    ecoli3 50 82.12 83.53 83.67
    yeast-0-5-6-7-9_vs_4 50 68.31 69.72 71.3
    glass-0-1-6_vs_2 100 72.71 72.72 72.76
    yeast-1_vs_7 100 70.11 70.71 71.03
    page-blocks-1-3_vs_4 100 95.49 96.06 97.53
    glass5 100 94.05 94.28 96.49
    yeast5 300 85.16 86.48 87.78
    yeast6 300 77.35 77.58 77.61
    下载: 导出CSV

    表 4  3种算法结果比较

    隐层节点数 G-mean/%
    ELM 折交叉验证的EN-ELM 基于分层交叉验证的EN-ELM
    30 84.86 85.58 85.58
    50 91.95 93.42 94.15
    80 98.32 98.52 99.24
    下载: 导出CSV
  • [1] ZONG W W, HUANG G B, CHEN Y Q. Weighted Extreme Learning Machine for Imbalance Learning[J]. Neurocomputing, 2013, 101:229-242. doi: 10.1016/j.neucom.2012.08.010
    [2] ZHANG Y, LIU B, CAI J, et al. Ensemble Weighted Extreme Learning Machine for Imbalanced Data Classification Based on Differential Evolution[J]. Neural Computing and Applications, 2017, 28(S1):259-267. doi: 10.1007/s00521-016-2342-4
    [3] HE H B, GARCIA E A. Learning from Imbalanced Data[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(9):1263-1284. doi: 10.1109/TKDE.2008.239
    [4] TANG Y C, ZHANG Y Q, CHAWLA N V, et al. SVMs Modeling for Highly Imbalanced Classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2009, 39(1):281-288. doi: 10.1109/TSMCB.2008.2002909
    [5] LIU X Y, WU J X, ZHOU Z H. Exploratory Undersampling for Class-Imbalance Learning[C]//Sixth International Conference on Data Mining (ICDM'06). Hong Kong, China: IEEE, 2006: 1-5.
    [6] 汪璇, 谢德体, 吕家恪, 等.集成GASA混合学习策略的BP神经网络优化研究[J].西南大学学报(自然科学版), 2007, 29(7):168-171. doi: http://xbgjxt.swu.edu.cn/article/id/jsunsxnnydxxb200707034
    [7] 李俊唐, 缑纯良, 何兴.基于神经网络的UWB室内定位算法[J].西南师范大学学报(自然科学版), 2018, 43(6):116-120. doi: http://www.cnki.com.cn/Article/CJFDTotal-XNZK201806020.htm
    [8] 季亚男, 刘光远, 陈通, 等.运动模糊图像经典复原算法[J].西南大学学报(自然科学版), 2018, 40(8):162-171. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xdzk.2018.08.022
    [9] 朱航涛, 王丽丹, 段书凯, 等.基于神经元晶体管和忆阻器的Hopfield神经网络及其在联想记忆中的应用[J].西南大学学报(自然科学版), 2018, 40(2):157-166. doi: http://xbgjxt.swu.edu.cn/article/doi/10.13718/j.cnki.xdzk.2018.02.022
    [10] 周志华, 陈世福.神经网络集成[J].计算机学报, 2002, 25(1):1-8. doi: 10.3321/j.issn:0254-4164.2002.01.001
    [11] MAO S S, JIAO L C, XIONG L, et al. Greedy Optimization Classifiers Ensemble Based on Diversity[J]. Pattern Recognition, 2011, 44(6):1245-1261. doi: 10.1016/j.patcog.2010.11.007
    [12] doi: http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC0210233470/ ZHOU Z H. When Semi-supervised Learning Meets Ensemble Learning[J]. Frontiers of Electrical and Electronic Engineering in China, 2011, 6(1):6-16.
    [13] doi: http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=2c3aaf1a8dcf9feccf1a13b8445c697a KUNCHEVA L I, WHITAKER C J. Measures of Diversity in Classifier Ensembles and Their Relationship with the Ensemble Accuracy[J]. Machine Learning, 2003, 51(2):181-207.
    [14] KIM M J, KANG D K. Classifiers Selection in Ensembles Using Genetic Algorithms for Bankruptcy Prediction[J]. Expert Systems With Applications, 2012, 39(10):9308-9314. doi: 10.1016/j.eswa.2012.02.072
    [15] HUANG G B, ZHU Q Y, SIEW C K. Extreme Learning Machine: a New Learning Scheme of Feedforward Neural Networks[C]//2004 IEEE International Joint Conference on Neural Networks. Budapest, Hungary: IEEE, 2004: 985-990.
    [16] doi: http://yadda.icm.edu.pl/yadda/element/bwmeta1.element.ieee-000006035797 HUANG G B, ZHOU H, DING X, et al. Extreme Learning Machine for Regression and Multiclass Classification[J]. IEEE Transactions on Systems Man & Cybernetics, Part B (Cybernetics). 2012, 42(2):513.
    [17] HANSEN L K, SALAMON P. Neural Network Ensembles[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(10):993-1001. doi: 10.1109/34.58871
    [18] ZHOU Z H, WU J X, TANG W. Corrigendum to Ensembling Neural Networks:Many could be Better than All[J]. Artificial Intelligence, 2010, 174(18):1570. doi: 10.1016/j.artint.2010.10.001
    [19] doi: http://d.old.wanfangdata.com.cn/NSTLQK/10.1016-j.neucom.2009.02.013/ LAN Y, SOH Y C, HUANG G B. Ensemble of Online Sequential Extreme Learning Machine[J]. Neurocomputing, 2009, 72(13/15):3391-3395.
    [20] doi: http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0224927194/ CAO J W, LIN Z P, HUANG G B, et al. Voting Based Extreme Learning Machine[J]. Information Sciences, 2012, 185(1):66-77.
    [21] LI K, KONG X F, LU Z, et al. Boosting Weighted ELM for Imbalanced Learning[J]. Neurocomputing, 2014, 128:15-21. doi: 10.1016/j.neucom.2013.05.051
    [22] LIU N, WANG H. Ensemble Based Extreme Learning Machine[J]. IEEE Signal Processing Letters, 2010, 17(8):754-757. doi: 10.1109/LSP.2010.2053356
    [23] CAO J W, LIN Z P, HUANG G B. Self-Adaptive Evolutionary Extreme Learning Machine[J]. Neural Processing Letters, 2012, 36(3):285-305. doi: 10.1007/s11063-012-9236-y
    [24] LIANG N Y, SARATCHANDRAN P, HUANG G B, et al. Classification of Mental Tasks from Eeg Signals Using Extreme Learning Machine[J]. International Journal of Neural Systems, 2006, 16(1):29-38. doi: 10.1142/S0129065706000482
  • 加载中
图( 3) 表( 5)
计量
  • 文章访问数:  2020
  • HTML全文浏览数:  2020
  • PDF下载数:  168
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-01-21
  • 刊出日期:  2020-06-01

改进的超限学习机及其在不平衡数据中的应用

    通讯作者: 王丽丹, 教授, 博士研究生导师; 
    作者简介: 李晗缦(1995-), 女, 硕士研究生, 主要从事神经网络和机器学习等方面的研究
  • 1. 西南大学 电子与信息工程学院, 重庆 400715
  • 2. 智能传动与控制技术国家与地方联合工程实验室, 重庆 400715
  • 3. 智能计算与智能控制重庆市重点实验室, 重庆 400715
  • 收稿日期:  2019-01-21
基金项目:  国家自然科学基金项目（61571372，61672436）；中央高校基本科研业务费专项资金项目（XDJK2016A001，XDJK2017A005）

摘要: 超限学习机（ELM）作为一种简单高效的学习算法被广泛应用于分类和拟合问题中.但是ELM在训练过程中逼近所有的样本容易造成过拟合，并且单个的ELM在不平衡数据分类上效果欠佳.因此，本文提出了一种新的基于分层交叉验证的集成超限学习机，该算法在训练阶段将集成学习和分层交叉验证相结合：①集成学习通过将若干个网络组合大大提高分类性能；②分层交叉验证最大程度学习样本的分布特点.基于KEEL数据库的不平衡数据分类问题的实验表明，新提出的算法更加稳定并且有更高的分类性能.

English Abstract

    全文HTML

  • 不平衡数据的应用场景出现在生活的方方面面，如搜索引擎的点击预测，电子商务领域的商品推荐，信用卡欺诈检测，网络攻击识别等[1].不平衡数据分类问题也成为机器学习领域一个重要研究课题.简单来说，不平衡数据分类问题就是其中一类或几类的数据占总数的比例远远大于其他类的数据.当遇到这类问题时，应该更关注数据量较少的类别，因为数据量越少包含的信息量越多[2].

    然而很多经典的学习算法例如决策树、支持向量机以及K-近邻法等都是基于平衡或基本平衡数据产生的，在计算时往往更关注数据量多的类别而忽略数据量少的类别[3-4]，即使将所有的数据都划分为多数的类别也能取得不错的效果.为了解决这一问题，很多用于不平衡数据分类的算法被提出.其中，欠抽样和过抽样应用最为广泛.通过减少一部分大比例数据以及扩充小比例数据，使数据重新分布，在一定程度上减少数据分布的不平衡性[5].加权学习作为另一种样本再平衡方法也可以解决这一问题.除此之外，神经网络集成也是一种广泛应用的解决不平衡数据分类问题的方法.神经网络在实际中有广泛的应用，汪璇等[6]将集成GASA混合学习策略与BP神经网络相结合应用在农作物虫情预测；李俊唐等[7]将神经网络和UWB结合起来用于室内定位；季亚男等[8]在运动模糊图像退化模型的基础上分析了模糊参数在已知和未知两种情况下模糊图像的PSF的确定方法；朱航涛等[9]将神经元晶体管和忆阻器的Hopfield神经网络用于联想记忆.神经网络集成简单来说就是训练多个基础网络，即基础分类器，再将它们集成在一起[10].集成学习可以减少过拟合，提高网络泛化能力.影响集成学习算法性能的主要因素有2个：基本分类器的精度和基本分类器之间的多样性[11-14].超限学习机(ELM)是由黄广斌等[15-16]提出的一种基于单隐层前馈神经网络的算法，它通过随机产生输入权重以及隐层结点的偏差，大大提高了训练速度，不需要在迭代过程中调整参数. ELM与其他传统神经网络算法相比具有显著的优越性，用ELM作为集成网络的基础分类器可以保证单个网络的精度.但是由于在训练阶段需要训练所有样本，单个的ELM依然存在着过拟合以及泛化能力低的缺点.

    将多个ELM结合起来可以解决上述问题[17-18].因为ELM的优越性，许多基于ELM的集成算法被提出. Lan等人[19]将多个在线的ELM(OS-ELM)的结果取平均值作为集成网络的结果；Cao等人[20]提出了基于投票的ELM集成学习；Li等人[21]将加权的ELM无缝嵌入到改进的Adaboost模型中，提出了一种增强加权的ELM；Liu等人[22]提出了一种基于ELM和K折交叉验证的集成算法(EN-ELM)，将集成学习和K折交叉验证结合起来.在训练过程中，将训练样本平均分为K折，依次选取其中的1折作为验证集，剩余的(K-1)折作为训练集，用这样的方法可以减小过拟合.但是这种方法也存在问题，当各类样本量差异较大时，简单地均分样本可能会破坏样本的比例，导致某1折中只含有比例较大的一类样本.不能有效地学习到测试集数据的特点，导致模型准确率较低.

    采用分层交叉验证的方法可以很好地解决这一问题.本文提出了一种基于分层交叉验证的集成超限学习机，将分层交叉验证与ELM结合起来作为集成网络的基础分类器.分层交叉验证也就是在划分训练样本时，令每一折的样本中都保持着原始数据中各个类别的比例关系，再进行交叉验证，最大程度地学习样本的分布特点，减小偶然性，提高基础分类器的准确率和泛化能力.并且在每一个基础分类器中根据训练结果G-mean调整输入权重和隐层偏差，找到令训练误差最小的输入权重和隐层偏差.另外，将多个多样的ELM集合起来提高了网络的分类能力.实验结果表明，与其他分类方法相比，该方法具有更好的分类性能.

1.   集成超限学习机和分层交叉验证

    1.1.   集成超限学习机

  • 超限学习机是由黄广斌等提出的一种基于单隐层前馈神经网络的算法.与其他基于梯度下降的算法不同，ELM在训练过程中的输入权重和隐层偏差随机产生，输出权重由最小二乘法计算得到.不需要在迭代过程中调整参数，大大简化了计算，提高了训练速度.

    对于N个任意不同的训练集(xj，tj)，xj∈Rn，tj∈Rm，j=1，2，3，…，N，其中xj表示输入数据向量，tj表示每个样本的目标向量.

    假设隐藏层有Ñ个神经元，那么ELM的输出如公式(1)所示：

    其中，wi=[wi1，wi2，…win]T和βi=[βi1，βi2，…βin]T分别表示输入权重和输出权重. bi和g(x)分别表示隐层节点的偏差和激活函数. oj是第j个节点的输出.

    超限学习机表示一个单隐层前馈神经网络可以无误差地逼近目标输出，也就是$\sum\limits_{j = 1}^N {\left\| {{o_j} - {t_j}} \right\|} $=0[23].存在βi，wi，bi令

    公式(2)可以写成如下形式：

    这里H表示隐层的输出矩阵；T=[t1，t2，…tN]T表示网络的目标输出.

    公式(3)是一个线性系统，输出权重可以由最小二乘法计算得到，方法如下：

    这里H+表示隐层输出矩阵H的Moore-Penrose伪逆矩阵.方程(4)中的解表明ELM在分类和回归问题上具有良好的泛化性能[24].

    Hansen和Salamon证明，通过训练多个神经网络并将其结果进行合成，可以显著地提高神经网络系统的泛化能力.假设每个ELM网络的输出结果为o(i)(xj)，i=1，…，P，P为集成网络中ELM的个数，那么，

    就是集成网络的输出结果.

    • 1.2.   分层交叉验证

  • 交叉验证法是指将整体数据集平均划分为K折，先取其中1折子集数据作为验证集，剩下的(K-1)折子集数据作为训练集进行一次训练；之后再取另外1折子集数据作为验证集，剩下的(K-1)折子集数据为训练集再进行一次训练，不断往复，最后重复K次的过程，一般称之为K折交叉检验[18].交叉检验是我们进行参数调整过程中一个非常重要的方法，但实际上，这样的做法存在一定的问题.由于采取的是平均划分，也就是完全随机抽样，这就可能会因为抽样划分的问题而改变原有的数据分布，不能使网络学习测试样本的分布特点，导致测试精度低.

    分层交叉验证属于交叉验证的一种.在划分数据集时，令每1折中都保持着原始数据中各个类别的比例关系，可以使得训练集和验证集的数据分布与测试集相同.特别是当样本数据不平衡时，简单的K折交叉验证可能导致划分时某1折的一类数据很少，甚至为0，降低了判别的准确性.

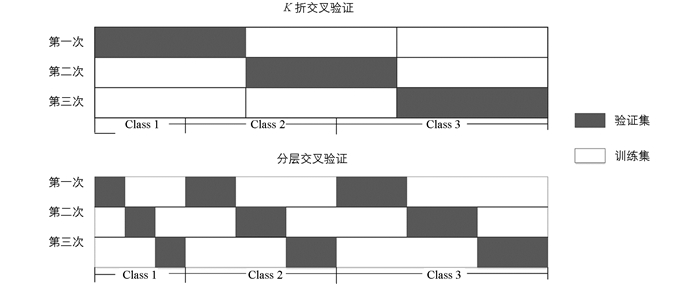
    以3折交叉验证为例，假设数据集共3类，分别为class1、class2和class3，并且3类比例各不相同，3折分层交叉验证与交叉验证区别如图 1所示.

2.   基于分层交叉验证的集成超限学习机

  • ELM算法通过随机选择隐含节点的权重和偏差，大大缩短了学习时间.然而，随机产生的参数不包含输入样本的特征，可能并不是最优的，从而降低泛化性能.因此，本文提出构造多个分类器的集合，每个分类器的参数根据特定准则更新，然后作出测试样本的决策.基于分层交叉验证的集成ELM算法如算法1所示.分层交叉验证算法贯穿整个学习过程.一方面，分层交叉验证的方法防止了过拟合，充分学习了样本分布特征；另一方面，集成算法提高了测试的稳定性和准确性.

    • 2.1.   样本分层

  • 假设共有R类样本，在新提出的算法中，将所有的样本都按照类别平均分为K个子集，一共得到R×K个子集.然后分别选取各个类的1个子集组成新的子集，一共组成K个子集，其中每个子集都由各个样本按比例组成.依次令其中1个子集作为验证集，其余的(K-1)个子集作为训练集.

    • 2.2.   初始化

  • 在初始化阶段，随机产生输入权重wi和隐层偏差bi，并将它们的值分别赋给$\mathop {{w_i}}\limits^ \wedge$和$\mathop {{b_i}}\limits^ \wedge$，用来存储最优的输入权重和隐层偏差.依次选取其中1个子集作为验证集，其余的(K-1)个子集作为训练集进行训练.经过K次交叉验证，将K次分类的结果按照评价标准计算得出的值(本文用G-mean作为评价标准)取平均赋给$G - \mathop m\limits^ \wedge ean$，在以后的每一个子分类器即每一次循环中，调整相应的输入权重和偏差，并将最好的值存储在$\mathop {{w_i}}\limits^ \wedge$和$\mathop {{b_i}}\limits^ \wedge$中.

    • 2.3.   权重更新和集成学习

  • 假设共有L个子分类器集成，那么网络会循环L次.在接下来的循环中，假如第l次产生的wil和bil可以取得更好的分类效果，即分类结果G-meanl > $G - \mathop m\limits^ \wedge ean$，那么就要把wil和bil分别赋值给$\mathop {{w_i}}\limits^ \wedge$和$\mathop {{b_i}}\limits^ \wedge$，并把G-meanl赋值给$G - \mathop m\limits^ \wedge ean$.这样，$\mathop {{w_i}}\limits^ \wedge$和$\mathop {{b_i}}\limits^ \wedge$就可以在迭代中保持最优的输入权重和隐层偏差.训练完成后，用训练得到的最优权重和偏差对测试样本进行分类.因为在训练过程中，训练集和验证集每类样本的分布和测试集一致，因此能更好地学习样本的特征，保证了测试的效果.

3.   实验结果和分析

    3.1.   不平衡数据分类评价指标

  • 精度是分类问题中评价模型性能的一个重要指标.但是对于不平衡数据来说，精度并不是一个很好的度量标准，因为正确率或错误率并不能表示不平衡数据下模型的表现，当把所有的数据都分为多数类时，也能达到一个较高的准确率.

    本文用G-mean代替准确率来评价分类的性能，能够同时考虑少数类的准确率和错误率. G-mean基于混淆矩阵计算，混淆矩阵如表 1所示.对二分类来说实验中可能出现4种结果，包括TP，TN，FP，FN，分别表示：正类数据正确分类数量；目标为正类，预测为负类；目标为负类，预测为正类；负类数据正确分类数量.

    G-mean计算公式为

    可以看出，G-mean可以同时考虑多数类和少数类的分类准确率，当少数类准确率很低时，G-mean也很低.

    • 3.2.   实验数据

  • 为了将本文所提出的基于分层交叉验证的集成超限学习机与其他学习算法进行比较，用Keel数据集库中的12个二值分类数据集进行实验. 表 2给出了按不平衡率升序排列的12个数据集的参数，包括其样本数量、特征参数和不平衡率.

    • 3.3.   实验结果和分析

  • 为了证明本文算法的优越性，我们将基于分层交叉验证的集成超限学习机(基于分层交叉验证的EN-ELM)与K折交叉验证的集成超限学习机(K折交叉验证的EN-ELM)以及未集成的超限学习机(ELM)进行比较. K折交叉验证的集成超限学习机就是在算法的初始化和循环中都采用K折交叉验证，将训练样本平均分为K折.未集成的超限学习机就是传统的没有集成的超限学习机.

    在数据分类实验中，3种算法的激活函数都采用Sigmoid函数.分层交叉验证的EN-ELM以及K折交叉验证的EN-ELM实验中，对于每个数据集，我们使用10倍交叉验证，基础网络的数量为10.根据样本不平衡率的不同，分类难度增加，本文设置了3种隐层节点数量，分别为50，100以及300.同一类样本的3种算法选用相同的隐层节点数量.取20次实验的平均值作为最终结果.

    在12个数据集上测试了本文算法和2种比较算法，并将最终的G-mean及相应的隐层节点数记录在表 3中.每个数据集的最佳性能结果以粗体显示.从表 3的结果可以看出，未集成的ELM在10个数据集上都取得了最低值.因此，集成学习比未集成学习有明显的优势，有助于提高分类性能.

    另外，基于分层交叉验证的EN-ELM在大多数数据集中都取得了最优的效果，只有在haberman和glass6中略低于其他2种算法，这可能是由于样本简单且不平衡率比较低，并不能完全体现分层交叉验证的优势.另外，在ecoli3，glass-0-1-6_vs_2以及yeast6中，基于分层交叉验证的EN-ELM相较于其他2种算法的优势不是特别明显，但从整体来看，基于分层交叉验证的EN-ELM对不平衡数据有很强的分类性能.

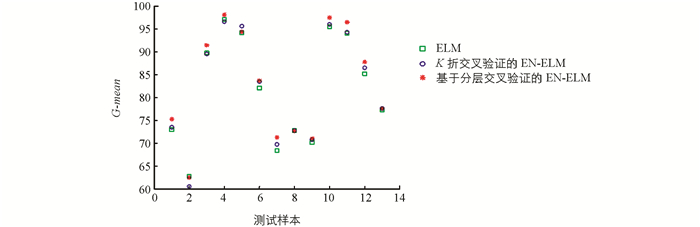
    此外，本文还用散点图更清晰地展示了实验结果.由图 2可以看出，基于分层交叉验证的EN-ELM对不同数据集分类的结果更集中在上半部分，在多数数据集中都有更好的效果，说明网络有较强的泛化能力.

    另外，本文还用加州理工学院的数据库Leaves 1999对算法进行了验证. Leaves 1999共包含3种、共186张在不同背景下拍摄的叶子照片，大小为896 mm×592 mm.因为G-mean只能衡量二分类问题，因此我们选取了3种叶子中的2种进行实验，并且2种叶子的数量比例为2:1.分别选取2种叶子的部分照片，如图 3所示.

    在实验中，3种算法的激活函数都采用Sigmoid函数.在分层交叉验证的EN-ELM以及K折交叉验证的EN-ELM实验中，采用10倍交叉验证，基础网络的数量为10，隐层节点数量分别为30，50以及80，取20次实验的平均值作为最终结果.为了计算方便，每张图片的大小设置为32×32.

    从表 4的实验结果可以看出，对于图像的分类试验，改进的算法依然可以取得很好的实验效果，不需要很多的隐层节点，就可以达到较高的精度，这也是没有改进的ELM算法目前欠缺的地方.虽然这种方法会使网络训练时间增加一些，但是分类精度也获得了较大的提高.

4.   结论

  • 本文提出了一种基于分层交叉验证的集成超限学习机，将集成学习方法和分层交叉验证策略引入到网络训练过程中.集成方法是解决不平衡分类问题，增强泛化能力的有效方法之一，分层交叉验证可以使样本划分更公平，减少过拟合.新提出的基于分层交叉验证的集成超限学习机综合了上述2种方法的优点，以减轻过度拟合，提高泛化能力，增强对不平衡数据的分类能力.实验结果表明，基于分层交叉验证的EN-ELM算法在不平衡数据以及不平衡图像分类中优于传统的ELM算法和K折交叉验证的EN-ELM，取得了不错的效果.

参考文献 (24)

目录

版权所有：西南大学学报（自然科学版）

地址：重庆市北碚区西南大学 电话：023-68254576, 68252540, 68366165,68366917 电子邮箱：lkxb@swu.edu.cn

本系统由北京仁和汇智信息技术有限公司开发

/

返回文章
返回