-
伴随着通讯网络的发展,网络被引入到控制系统中来,不仅减少了系统连线,而且降低了系统成本,网络控制系统也应运而生并成为国内外控制界研究的热点之一[1-5].
针对网络系统的研究大多集中在网络诱导时延、数据包丢失、网络带宽受限等方面[6-7],而且关于网络系统稳定方面的研究主要采用Lapunov稳定性理论讨论系统的渐近稳定性,对系统的有限时间稳定性的研究却较少[8]. 在实际工程中,由于网络系统的工作时间一般比较短暂,人们除了对系统的渐近稳定性感兴趣外,更关心的往往是系统满足一定的暂态性能要求. 因此,对网络系统的有限时间性能分析与控制综合就显得尤为重要.
上世纪50年代,文献[9]率先提出了短时间稳定的概念. 随后,文献[10]在有限时间理论中引入线性矩阵不等式方法,极大地推动了有限时间理论的发展. 文献[11]将网络控制系统定义为带有丢包和时延等网络缺陷的控制系统,利用Bernoulli分布序列对带有随机丢包的网络系统进行建模. 在此基础上,利用线性矩阵不等式方法,得到系统有限时间有界的充分条件. 文献[12]建立了具有范数有界扰动的线性离散时延系统鲁棒有限时间稳定的充分条件,并利用线性矩阵不等式方法给出了时延相关的充分条件. 文献[13]研究了不确定非完整系统的有限时间镇定问题. 上述研究成果主要针对传统的点对点系统,关于网络系统有限时间稳定性分析及控制方面的结果却极少见报道. 文献[14]研究了一类具有短时变时延和采样抖动的网络系统的有限时间控制问题,利用鲁棒控制方法解决有限时间稳定性问题. 文献[15]把预测控制方法引入到网络系统中,得到了有限时间稳定的充分条件.
然而,以往为数不多的关于网络系统有限时间控制的研究结果也是针对确定性网络系统的研究,缺少对外界干扰、网络诱导时延、数据包丢失等因素的分析. 因此,研究受扰网络系统的有限时间稳定性分析与控制问题具有较强的实际意义. 本文旨在研究外界干扰影响下网络系统的暂态性能分析与控制设计问题. 利用有限时间理论和线性矩阵不等式方法,探寻系统有限时间稳定性条件及控制器设计方法,为减少外界干扰对网络系统的影响、提高系统暂态性能提供有效方法与途径.
全文HTML
-
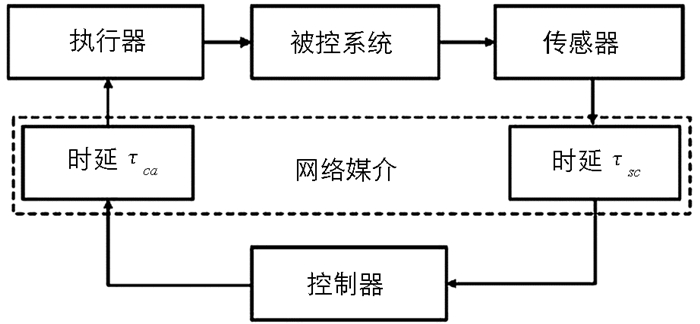
考虑如图 1所示的不确定网络控制系统
其中:常数矩阵A,
$ \boldsymbol{A}_{h} \in \mathbb{R}^{n \times n}, \boldsymbol{B} \in \mathbb{R}^{n \times m}, \boldsymbol{B}_{1} \in \mathbb{R}^{n \times l} $ 是系统的状态矩阵和控制矩阵;$ \boldsymbol{x}\left( t \right)\in {{\mathbb{R}}^{n}} $ 代表系统状态;$ \boldsymbol{u}\left( t \right)\in {{\mathbb{R}}^{m}} $ 代表控制;h代表系统状态时延;$ \boldsymbol{\omega}\left( t \right)\in {{\mathbb{R}}^{l}} $ 代表满足下面不等式条件的外部干扰$ \mathit{\pmb{\Delta}} \boldsymbol{A}(t), \mathit{\pmb{\Delta}} \boldsymbol{A}_{h}(t) \in \mathbb{R}^{n \times n}, \mathit{\pmb{\Delta}} \boldsymbol{B}(t) \in \mathbb{R}^{n \times m}, \mathit{\pmb{\Delta}} \boldsymbol{B}_{1}(t) \in \mathbb{R}^{n \times l} $ 是代表不确定性的未知矩阵满足其中D1,D2,D3,D4,E1,E2,E3,E4是具有合适维数的常数矩阵,F(t)是具有合适维数的未知时变矩阵满足
由于网络媒介的引入,不可避免会出现网络诱导时延τ=τsc+τca,因此网络系统(1)变为
设计网络系统(3)的状态反馈控制器如下
其中K是待定的未知常数矩阵. 则闭环系统为
其中
-
引理1[16] 对已知的常数ε>0和矩阵D,E,F,其中F满足FTF≤I,则下面矩阵不等式成立
引理2[6] 线性矩阵不等式
等价于
其中Y(x)=YT(x), R(x)=RT(x)为对称矩阵.
定理1 对已知常数c1,c2,T>0(c1 < c2)和正定矩阵R,网络系统(3)是(c1,c2,T,R,d)有限时间镇定的,如果存在非负常数α≥0,正定矩阵
$ \boldsymbol{P} \in \mathbb{R}^{n \times n}, \boldsymbol{Q} \in \mathbb{R}^{n \times n}, \boldsymbol{T} \in \mathbb{R}^{n \times n}, \boldsymbol{S} \in \mathbb{R}^{l \times l} $ 和矩阵$ \boldsymbol{K}\in {{\mathbb{R}}^{m\times n}} $ 满足不等式其中λmax()和λmin()分别代表最大、最小特征值,
证 对网络系统(3),选取如下Lyapunov泛函
沿闭环系统(5)的状态轨迹,有
其中
由条件(6a),可得
在(8)式左右两边乘以e-αt得到
从而
从0到t进行积分得到
由α≥0,做变换
$ \widetilde{\boldsymbol{P}}=\boldsymbol{R}^{-\frac{1}{2}} \boldsymbol{P R}^{-\frac{1}{2}}, \widetilde{\boldsymbol{Q}}=\boldsymbol{R}^{-\frac{1}{2}} \boldsymbol{Q R}^{-\frac{1}{2}}, \widetilde{\boldsymbol{T}}=\boldsymbol{R}^{-\frac{1}{2}} \boldsymbol{T R}^{-\frac{1}{2}} $ ,得到如下不等式:另外,容易知道
由(10)和(11),可得
由条件(6b)和不等式(12)得到
注1 基于有限时间稳定性理论,利用线性矩阵不等式方法,把网络系统(1)有限时间稳定性条件转化为定理1中的矩阵不等式(6a)和一个不等式约束(6b). 然而,由于(6a)是非线性的,因此不能借助MATLAB软件进行直接求解,需要进一步进行等价变换.
-
定理2 对已知常数c1,c2,T>0(c1 < c2)和正定矩阵R,选取状态反馈控制器
$ \boldsymbol{u}\left( t \right)={\boldsymbol{\bar{K}}}{{\boldsymbol{X}}^{-1}}\boldsymbol{x}\left( t \right) $ ,如果存在常数α≥0,λi>0,i=1,2,3,4. n×n矩阵X>0,Q>0,T>0, l×l矩阵S和m×n矩阵K使得如下线性矩阵不等式成立,则网络系统(3)是(c1,c2,T,R,d)有限时间镇定的,其中
证 下面主要证明矩阵不等式(6a)等价于线性矩阵不等式(13a).
把式(5)代入(6a)得到
其中
由引理1可知不等式(14)等价于
其中
由引理2可知不等式(15)等价于
其中
在不等式(16)两边分别乘分块对角矩阵
可知不等式(6a)等价于
其中
令
$ \boldsymbol{X}=\boldsymbol{P}^{-1}, \overline{\boldsymbol{K}}=\boldsymbol{K} \boldsymbol{P}^{-1}, \overline{\boldsymbol{Q}}=\boldsymbol{P}^{-1} \boldsymbol{Q} \boldsymbol{P}^{-1}, \overline{\boldsymbol{T}}=\boldsymbol{P}^{-1} \boldsymbol{T} \boldsymbol{P}^{-1} $ ,则不等式(17)等价于(13a). 另外,令$ \widetilde{\boldsymbol{X}}=\boldsymbol{R}^{-\frac{1}{2}} \bf{X} \boldsymbol{R}^{-\frac{1}{2}}, \widetilde{\boldsymbol{Q}}=\boldsymbol{R}^{-\frac{1}{2}} \boldsymbol{Q} \boldsymbol{R}^{-\frac{1}{2}}, \widetilde{\boldsymbol{T}}=\boldsymbol{R}^{-\frac{1}{2}} \boldsymbol{T} \boldsymbol{R}^{-\frac{1}{2}} $ ,由于R是正定矩阵,因此由不等式(13b)-(13e)可知
由引理2可知不等式(13f)等价于
由(18)式和条件(6b)可得
由不等式(19)-(20),容易知道不等式(6b)成立.
注2 在定理2中,利用矩阵不等式技术把定理1中的非线性矩阵不等式等价转化为线性矩阵不等式组(13a)-(13f),从而可以借助MATLAB软件直接求解,也正因为此,定理2的结论更加方便地适用于工程实际,具有一定的实际应用价值.
2.1. 有限时间镇定条件
2.2. 有限时间控制器设计
-
算例1 在不确定网络系统(3)中选取系统参数如下
选取c1=0.5,α=0.8,T=2,R=I2,求解线性矩阵不等式(13),得到状态反馈控制器
选取初始条件为
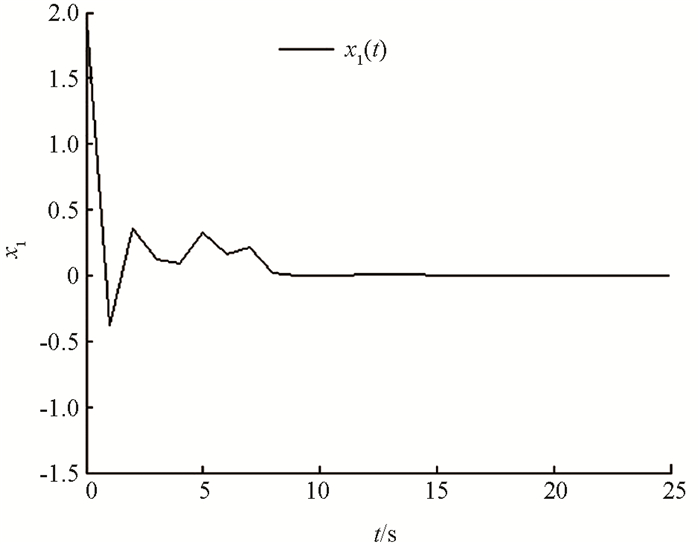
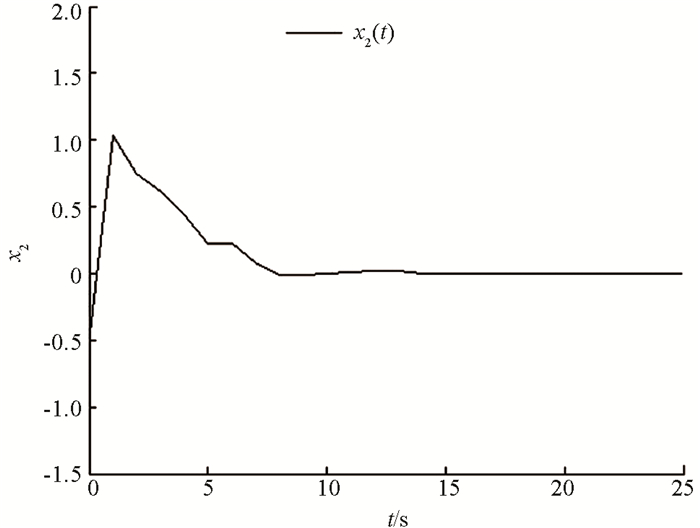
由图 2,3,系统状态在8 s时间内收敛于0,因此系统状态是有限时间稳定的.
算例2
$ \frac{1}{4} $ 车身主动悬架系统可以简化为带弹簧、阻尼器和执行器的2自由度振动系统. 根据牛顿第二定律,得到了$ \frac{1}{4} $ 车体主动悬架模型的运动方程为[16]其中:m1,m2分别是弹簧的上质量和下质量;K1,K2分别是悬架弹簧刚度和轮胎刚度;b是等效悬挂阻尼系数;u是执行器产生的作用力. 选择状态向量为
$ \boldsymbol{x}=\left[\begin{array}{llll} X_{1} & X_{2} & \dot{X}_{1} & \dot{X}_{2} \end{array}\right]^{\mathrm{T}} $ ,控制输入为$ \boldsymbol{u}^{\prime}=\left[\begin{array}{ll} u & X_{0} \end{array}\right]^{\mathrm{T}} $ ,其中X1,X2分别是车身和悬架的垂直位移,X0是道路输入. 车体的垂直位移为X1,悬挂垂直位移为X2,车体垂直速度为$ {{{\dot{X}}}_{1}} $ ,悬挂垂直速度为$ {{{\dot{X}}}_{2}} $ .从而得到系统的状态空间形式
其中
考虑到系统可能会受到不确定性外界干扰和执行器传输时延的影响,考虑如下形式的2自由度振动系统
其中
利用PID控制方法进行MATLAB仿真模拟,用于建模和仿真的主动悬架参数如下
采用阶跃信号作为系统的参考输入,通过改变P值来实现PID控制对主动悬架的影响. 为了比较PID控制器对系统状态的仿真结果,采用本文提出的方法求解线性矩阵不等式(13),得到状态反馈控制器
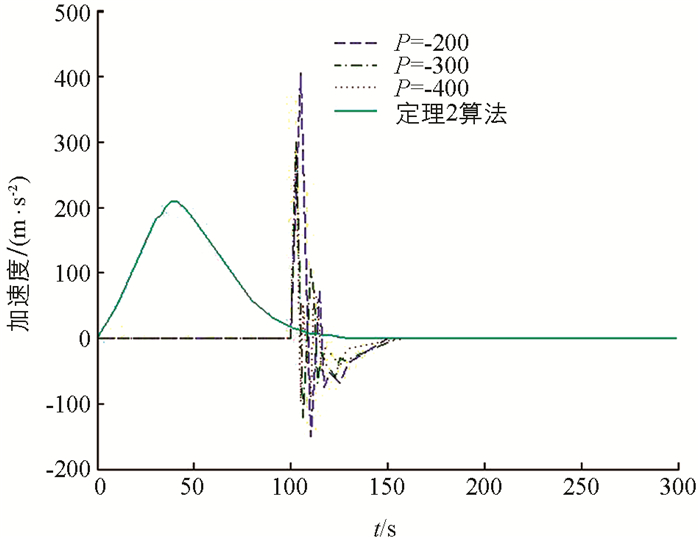
分别选取P=-200,-300,-400,对系统进行仿真,同时利用定理2中算法进行仿真,得到模拟加速度和时间之间的关系如图 4所示.
从图 4中可以看出悬架输出的最大幅度范围随P绝对值的增大而减小. 通过调节P值,PID控制可以有效地吸收悬架的振动输出. 但随着P的绝对值逐渐增大,系统振动频率也趋于增大,使得系统的收敛时间增大,稳定性变差. 因此,PID控制虽然能够有效地吸收悬架的振动输出,但不能保证系统的收敛速度. 图中点划线是利用定理2中算法得到的状态响应曲线. 从图 4可以看出,点划线的收敛速度和平滑程度都比虚线好. 结果表明,该控制器能有效地改善系统的动态性能,本文提出的算法优于PID控制方法.
-
本文把有限时间稳定性分析与控制方法引入到网络系统中,主要做了如下工作:充分考虑到网络诱导时延对系统的影响,建立更加切合实际的网络系统数学模型;结合有限时间稳定性理论,利用线性矩阵不等式方法探寻系统有限时间稳定的充分条件;利用矩阵不等式变换技巧把非线性的稳定性条件等价转化为线性的矩阵不等式组形式,并同时得到了系统有限时间状态反馈控制器设计方法. 由于得到的条件可以通过MATLAB十分方便地求解,因此该方法更加容易应用到工程实际. 下一步的工作将尝试对带有数据包丢失的网络系统进行研究.



 下载:
下载: