亮度(I)和比率(α)特征的定义如下^[10-12]：

其中，R^*(i，j)，G^*(i，j)，B^*(i，j)分别表示图像第i行第j列像素RGB三通道的灰度值. N为通道数3.

原始减法直方图算法描述如算法1所示. 在步骤Step4-3中，最大梯度区间的中位点值：

V表示e_k中最小的非零波谷值，P表示e_k最右边峰值，参数C₁∈[0, 1]文献[9]取的经验值0.4.

从包含阴影和非阴影的土壤彩色图像中随机抽取60张构成20组图像，运用公式(1)、(2)将图像分别转换为I和α的灰度图.

图 1显示，土壤图像转换为α灰度图后，阴影与非阴影的区分度较低. 其余19组土壤图像有相同的结果. 对原始减法直方图算法分析，原始算法保留直方图的计算区间为64等份值域，阈值的搜索存在冗余，有效缩短阈值的搜索区间可降低时间复杂度；原始算法中参数C₁在[0, 1]区间内按一定步长进行实验搜索获得经验值0.4，对于土壤图像阴影检测不具科学性，鲁棒性差.

为了提升土壤图像阴影和非阴影的区分度，重构α为α'：

其中，τ为拉伸因子，τ∈^{[2, 3]}.

原始减法直方图算法中保留直方图的计算区间为64等份值域，存在冗余.

分别对I和α'特征的64等分直方图B₀和R'₀高斯平滑获得B和R'.

计算B和R'相邻频数比r

其中，H(i)，H(i+1)分别表示直方图在i和i+1位置的频数.

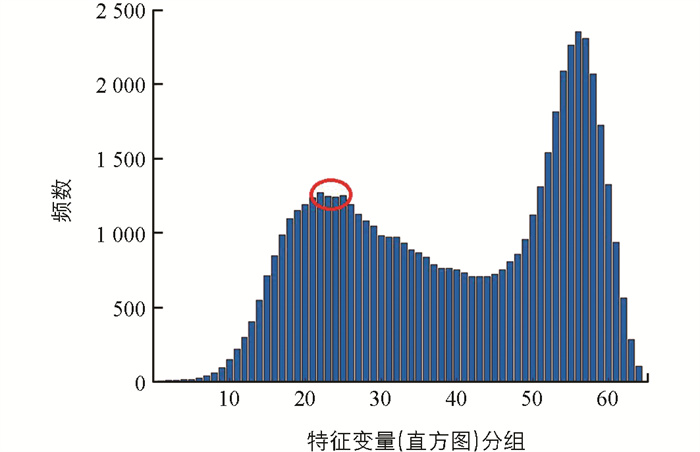
由于高斯平滑处理后的直方图仍可能出现如图 2红圈所示的伪谷，为了消除其对r_H的影响，对r_H进行平滑^[13-14]处理，具体平滑方法为

1) $\begin{array}{l} {\rm{if}}\ ({r_H}(i) < 0\& \& {r_H}(i + 1) > 0\& \& {r_H}(i + 2) < 0) \end{array}$

2) ${\rm{if}}\ ({r_H}(i) < 0\& \& {r_H}(i + 1) > 0\& \& {r_H}(i + 2) > 0\& \& {r_H}(i + 3) < 0)$

3) ${\rm{if}}\ ({r_H}(i) > 0\& \& {r_H}(i + 1) < 0\& \& {r_H}(i + 2) > 0)$

4) ${\rm{if}}\ ({r_H}(i) > 0\& \& {r_H}(i + 1) < 0\& \& {r_H}(i + 2) < 0\& \& {r_H}(i + 3) > 0)$

平滑后相邻频数比r直方图中，如果r_H(i)＜0 & & r_H(i+1)＞0，则i+1为波谷点. 顺序提取所有波谷点位置构成向量φ_H，并在向量φ_H的第一个元素前插入0作为第一个峰的位置起点，在最后一个元素后插入63作为最后一个峰的终点. 即φ_H为平滑后相邻频数比r直方图的完整波谷点向量，其任意相邻点构成区间上平滑后r直方图的波峰.

平滑后r直方图的每一个波峰对应于B和R'上的一个真正的波峰. 取φ_H中任意相邻点构成区间范围，分别计算B和R'直方图在该区间的面积：

其中，φ_H (j)、φ_H (j+1)为φ_H中相邻2个元素的值，H(k)表示B或R'第k个位置的对应频数；w表示直方图 64等份中1等份的长度.

分别对B和R'直方图求面积S，对面积S中最大的2个主峰的峰值点对应的64等分中位值构成区间$[pk_{{\rm{start}}}^B, pk_{{\rm{end}}}^B]$和$[pk_{{\rm{start}}}^{R'}, pk_{{\rm{end}}}^{R'}]$，即为非阴影和阴影分割阈值的搜索区间. 其中，$pk_{{\rm{start}}}^B$为I的非阴影主峰值点，$pk_{{\rm{end}}}^B$为I的阴影主峰值点，$pk_{{\rm{start}}}^{R'}$为α'的非阴影主峰值点，$pk_{{\rm{end}}}^{R'}$为α'的阴影主峰值点.

根据上述算法思想，获取I和α'特征的非阴影和阴影分割阈值搜索区间算法如下所示.

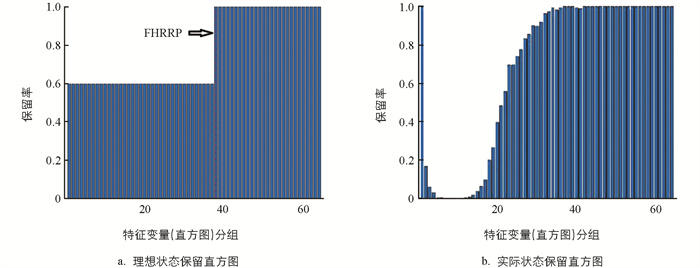
原始减法直方图算法理想状态保留直方图(如图 3a)，其最大梯度差的梯度区间中位点为F. 实际状态保留直方图(如图 3b)，以最大梯度差的梯度区间中位点为F，其结果不准确，影响分割效果. 为解决上述缺陷，重构保留直方图. 运用式(7)对保留直方图e_k进行拉伸，增大保留直方图最大梯度区间的梯度差.

其中，ω为拉伸因子，ω≥0.1，size为特征等份数64，tanh为双曲正切函数.

将e'_k连续5等份分为一组，第1组为[e'_k(0)，e'_k(4)]，第2组为[e'_k(5)，e'_k(9)]，…，第13组为[e'_k(60)，e'_k(63)]，第13组最后一位用0补齐；求第1组到第13组每一组中e'_k(i)的最大值；在13组中剔除最大值为0的组，从剩余组中找到最大值最小的那一组，其非0最小值所在e'_k中的位置即为非零波谷点v'. 保留直方图e'_k中v'右边的最大值位置为k'. 则高保留率点F'为

其中，Mid_T表示保留直方图中第i个等份的中位值点，e'_k(i)表示保留直方图中第i等份，i在[v'+1，k']范围内.

依据获得的I分割阈值搜索区间$[pk_{{\rm{start}}}^B, pk_{{\rm{end}}}^B]$，即$t{B_k}\left( {k = pk_{{\rm{start}}}^B, \cdots , pk_{{\rm{end}}}^B} \right)$，和α'分割阈值搜索区间$[pk_{{\rm{start}}}^{R'}, pk_{{\rm{end}}}^{R'}]$，即$t{R'_k}\left( {k = pk_{{\rm{start}}}^{R'}, \cdots , pk_{{\rm{end}}}^{R'}} \right)$分别获得其中每一个tB_k和tR'_k的保留直方图，并用式(8)分别求每个保留直方图对应的高保留率点F'_k.

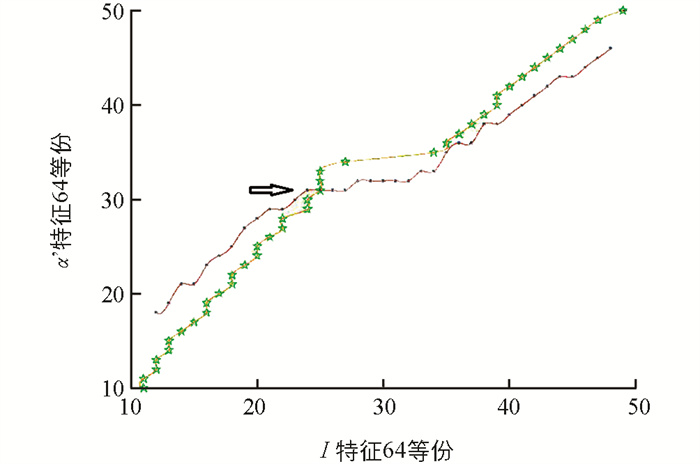
以tB_k为横坐标，对应的F'_k为纵坐标画点，依次将$\left( {k = pk_{{\rm{start}}}^B, \cdots , pk_{{\rm{end}}}^B} \right)$对应的点连接成一条折线. 同理，以tR'_k为横坐标，对应的F'_k为纵坐标画点，依次将$\left( {k = pk_{{\rm{start}}}^{R'}, \cdots , pk_{{\rm{end}}}^{R'}} \right)$对应的点连接成一条折线. 组合两坐标系(如图 4)，2条折线的交点对应值分别为I的分割阈值T_B和α'的分割阈值T_R'.

根据上述算法思想获得的阴影检测阈值搜索算法如算法3所示.

由算法3阴影检测阈值搜索算法可知，搜索I分割阈值T_B需要从$t{B_k} = pk_{{\rm{start}}}^B$位开始，计算保留直方图及其对应的F'_k，直到$t{B_k} = pk_{{\rm{end}}}^B$结束，遍历过程总共执行$pk_{{\rm{end}}}^B - pk_{{\rm{start}}}^B + 1$次. 同理，搜索α'分割阈值T_R'的遍历过程总共也需要执行$pk_{{\rm{end}}}^{R'} - pk_{{\rm{start}}}^{R'} + 1$次. 最坏的情形是：$pk_{{\rm{start}}}^B = t{B_0}$和$pk_{{\rm{end}}}^B = t{B_{63}}$，$pk_{{\rm{start}}}^{R'} = t{{R'}_0}$和$pk_{{\rm{end}}}^{R'} = t{{R'}_{63}}$，搜索次数为64*2次. 最好的情形是：$pk_{{\rm{end}}}^B = pk_{{\rm{start}}}^B$和$pk_{{\rm{end}}}^{R'} = pk_{{\rm{start}}}^{R'}$，搜索次数为0次，平均搜索次数为32*2次. 分割阈值交点(T_B，T_R')分别落在I和α'直方图双峰搜索区间内，搜索区间内的逐点搜索浪费了不必要的时间花销.

算法3阴影检测阈值搜索算法获得分割阈值T_B和T_R'为2条折线(如图 4)的交点. 通常情况下，2条折线有1个交点，一条折线的一端仅跨越另一条折线1次，连接每条折线端点的2条直线也相交. 因此，将折线相交近似为直线相交，逐步逼近折线交点，可减少搜索次数. 其方法是：首次取端点构成直线，获取交点，再用端点与交点的中位点在折线上的位置点替代端点重构直线，获取新的交点，这样反复直到搜索到折线交点.

取图 5a中①②③④点分别为端点(tB_left，F'_left_B)，(tB_right，F'_right_B)，(F'_left_R'，tR'_left)和(F'_right_R'，tR'_right).分别将①②和③④连成2条直线(如图 5b).

求得2条直线交点为(T_B，T_R'). 如图 5c，用(tB_left+T_B)/2更新tB_left及对应的F'，更新①；(tB_right+T_B)/2更新tB_right及对应的F'，更新②；同理，如图 5d所示，(tR'_left+T_R')/2更新tR'_left及对应的F'，更新③. (tR'_right+T_R')/2更新tR'_right及对应的F'，更新④.

将①与③和④进行比较，②与③和④进行比较，若相等停止迭代；若不相等则重构①②和③④连成2条直线，更新2条直线交点(T_B，T_R')，更新①②③④点，直到迭代停止. 迭代停止时的交点(T_B，T_R')即为最后的阴影检测阈值.

阴影检测阈值搜索最坏的情形是：$pk_{{\rm{start}}}^B{\rm{ = }}t{B_0}$和$pk_{{\rm{end}}}^B{\rm{ = }}t{B_{63}}$，$pk_{{\rm{start}}}^{R'}{\rm{ = }}t{{R'}_0}$和$pk_{{\rm{end}}}^{R'}{\rm{ = }}t{{R'}_{63}}$，即tB_k和tR'_k的全域搜索. 依据3.2的算法思想，每次迭代的搜索域折半，最坏的情形：在I搜索域最大长度是64，经过6次迭代到达折线交点；同理α'也经过6次迭代到达折线交点，合计计算保留直方图和F'_k的次数为12. 即12是阴影检测阈值搜索加速算法迭代次数的上确界.

最好的情形是：$pk_{{\rm{end}}}^B = pk_{{\rm{start}}}^B$和$pk_{{\rm{end}}}^{R'}{\rm{ = }}pk_{{\rm{start}}}^{R'}$，搜索次数为0次. 理论上平均搜索次数为6次迭代到达折线交点，获得分割阈值.

实际上，设I左右两主峰间距离间隔为dis_B，α'当前左右两主峰间距离间隔为dis_R'；每迭代一次dis_B减少一半，dis_R'也减少一半；迭代总次数为$n = \left\lceil {{\rm{lo}}{{\rm{g}}_2}di{s_B}} \right\rceil + \left\lceil {{\rm{lo}}{{\rm{g}}_2}di{s_{R'}}} \right\rceil $(向上取整). 通常，迭代4~8次到达折线交点，获得分割阈值. 上述结论也证明加速算法是收敛的.

根据重庆土壤分类与代码[DB50/T796-2017]^[15]，对重庆璧山区分布的4土属(暗紫泥、红棕紫泥、灰棕紫泥、黄棕紫泥)34土种，在野外自然环境下用土锹锹出耕层0~20 cm的土壤，拍摄土壤(心土)自然断口，使土壤区域位于图像中心位置，并占全图面积50%以上. 从已采集的共计342张土壤图像中，随机抽取60张在土壤区域存在部分阴影的土壤彩色图像，用文献[16]分割出土壤区域图像组成20组实验图像样本.

为了验证本文算法的有效性设计实验如下：

1) 阴影检测精度对比实验(实验1)：应用实验样本，进行本文算法2+算法3和本文算法2+算法4，文献[9]原始减法直方图算法(包括原始算法eSH和加速算法iSH算法)、文献[7]算法、文献[8]算法的对比实验，检测土壤彩色图像阴影，检验本文算法阴影检测精度，验证本文算法2+算法4计算的实际迭代次数与是否在理论(证明)最大迭代次数内的一致性问题.

2) 阴影检测效率对比实验(实验2)：应用实验样本，进行本文算法2+算法3和本文算法2+算法4，文献[9]原始减法直方图算法(包括原始算法eSH和加速算法iSH算法)、文献[7]算法、文献[8]算法的对比实验，检测土壤彩色图像阴影，检验本文算法阴影检测效率.

3) 全图为阴影或非阴影检测实验(实验3)：取土壤图像子块全图为阴影或非阴影(包括被人工用非阴影部分替换阴影部分像素的人工合成子图)，验证本文算法2对于全图为阴影或非阴影图像检测的有效性.

本文实验在Intel(R) Xeon(R) Silver 4114CPU @ 2.20GHz 2.19 GHz (2处理器)，内存64GB，显卡NVIDIA TITAN V，Windows 10专业工作站版64位，Visual Studio 2017，OpenCV 3.4.1环境下完成(未使用多CPU、GPU并行加速).

1) 阴影检测实验图像结果

对20组实验图像样本进行本文算法2+算法3和本文算法2+算法4、文献[9]原始减法直方图算法(包括原始算法eSH和加速算法iSH算法)、文献[7]算法、文献[8]算法的阴影检测对比实验. 随机选取No.3和No.15组实验样本，阴影检测结果如图 6所示.

2) 阴影检测实验数据结果

上述实验的阴影检测——分割阴影与非阴影精度(用亮度标准差评估)数据如表 1所示.

上述实验的阴影检测执行10次，平均时间花销如表 2所示.

1) 重构α'特征的有效性分析

阴影检测实验图像结果图 6(No.3组和No.15组样本)b，c，f，g显示：本文算法2+算法3和算法2+算法4使用重构的α'特征阴影检测，相比于文献[9]的eSH算法和iSH算法使用α特征阴影检测，本文改进的算法分割效果更好. 表 1显示：本文算法2+算法3和算法2+算法4对20组样本阴影检测，分割的阴影与非阴影的亮度标准差均值分别为23.987 1，24.542 8和24.713 7，24.200 2；文献[9]eSH算法和iSH算法对20组样本阴影检测，分割的阴影与非阴影的亮度标准差均值分别为15.996 0，51.773 1和21.091 9，52.367 9. 本文改进算法分割的非阴影亮度标准差值远小于文献[9]eSH算法和iSH算法分割的非阴影亮度标准差值，且其分割的阴影与非阴影的亮度标准差均值也远小于文献[9]的算法，说明文献[9]算法阴影分割存在不足，没有从非阴影中分割出来，本文改进算法的阴影检测精度更高. 上述结果证明，重构α'特征对土壤图像阴影检测是有效的.

2) 阴影检测精度分析

阴影检测实验图像结果图 6(No.3组和No.15组样本)d，e，f，g显示：文本算法2+算法3和算法2+算法4对20组样本阴影检测，相比于文献[7]算法和文献[8]算法，本文改进算法分割效果更好. 表 1显示：文献[7]算法和文献[8]对20组样本阴影检测，分割的阴影与非阴影的亮度标准差均值分别为18.036 2，41.665 5和20.851 7，33.930 6. 本文改进算法分割的非阴影亮度标准差值远小于文献[7-9]的对比算法分割的非阴影亮度标准差值，且其分割的阴影与非阴影的亮度标准差均值之和也都远小于对比算法，说明对比算法阴影分割不足，部分阴影没有从非阴影中分割出来，本文改进算法阴影检测精度更高.

3) 本文算法2+算法4的实际迭代次数结果分析

表 1显示：本文算法2+算法4对20组样本阴影检测的阈值搜索迭代次数为4~6次，本文3.3节理论证明阴影检测阈值搜索最大迭代次数为6次，实验结果证明算法计算的实际迭代次数在理论(证明)最大迭代次数内，与理论证明结果是一致的.

4) 2条分割阈值折线交点数的分析与处理

土壤图像可分为全图为阴影、全图为非阴影和包含部分阴影三类图像. 算法2可检测出全图为阴影或非阴影图像，不需继续阴影检测. 阴影检测是对包含部分阴影图像检测，是一个典型的二分类问题，通常2条分割阈值折线交点数为1. 由于受到土壤杂质等因素影响，极少数出现2条分割阈值折线交点数大于等于2的多个交点情形，选择其亮度标准差均值最小的交点分割阈值，实验结果证明是有效的.

5) 阴影检测时间效率分析

表 2显示：对20组样本执行10次阴影检测任务，本文算法2+算法3和算法2+算法4的平均时间花销分别为42.687±2.405、14.050±1.540；文献[9]eSH算法和iSH算法分别为61.016±3.171、4.718±0.570；文献[7]算法为1.897±0.169；文献[8]算法为1.142±0.129. 上述数据显示：本文原始算法——算法2+算法3比文献[9]原始算法——eSH算法快近1/3，文献[9]加速算法——iSH算法比本文加速算法——算法2+算法4快近3倍是因为iSH算法完全依赖于数据集计算的阴影检测经验值，在经验值附近搜索降低运行时间开销，而本文算法2+算法4是不需要任何先验知识的完全自适应单张图像阴影检测算法，是不需要任何人为参数的更先进的自适应算法. 文献[7]算法是自定义单测度的Otsu算法和文献[8]是利用HSI颜色空间数据定义一个测度(S-I)/(S+I)，根据建筑物阴影检测的经验值指定分割阈值进行阴影检测，尽管它们的耗时都非常低，但它们主要是用于建筑物阴影检测的，不适用于土壤图像阴影检测.

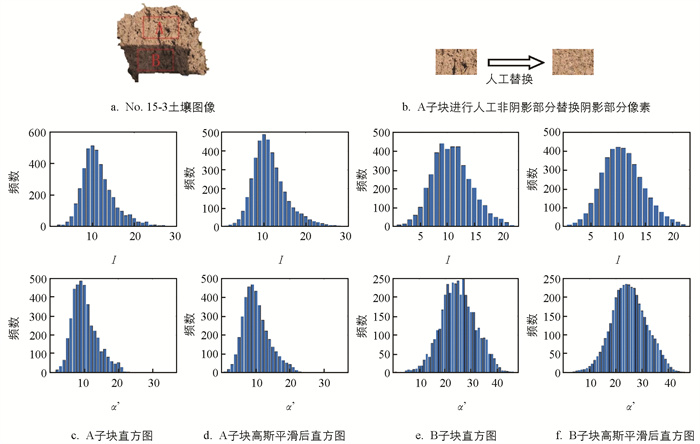
对20组土壤图像实验样本中取全图为阴影或非阴影的子块(如图 7). 在阴影和包含少量阴影的非阴影区域各取80*50像素大小的子块，对A子块中阴影像素用同子块中非阴影像素替换，人工合成非阴影子块A和阴影子块B作为检测样本，用算法2检测A、B子块的I和α'特征直方图.

图 7显示：非阴影子块A和阴影子块B的I和α'特征直方图呈现单峰结构. 如果检测为单峰结构说明土壤图像为全图非阴影土壤图像或全阴影土壤图像，无需进一步分割，可直接进入下一步切割为用于土种识别的子图，进行子图归一化和土种识别操作.

20组土壤图像实验样本中，对其他所有图像生成的非阴影和阴影子块检测，具有相同的检测结果.

本文对土壤图像阴影检测的典型二分类问题和基于I、α特征阴影检测的原始减法直方图算法进行研究，依据典型二分类问题分类特征的双峰特性，改进减法直方图算法用于土壤图像阴影检测.

1) 改进减法直方图算法将α特征重构为α'特征，提升该特征的双峰特性；改进减法直方图算法对获得的保留直方图进行拉伸，增大保留直方图的最大梯度差，使搜索保留直方图的最大梯度求解阈值变得更直观.

2) 改进减法直方图算法从左右峰值点开始搜索分割阈值，减少了搜索范围，比改进前减少了近1/3计算时间开销. 理论证明改进减法直方图加速算法，最坏情形计算保留直方图和F'_k的次数为12次，即减法直方图的上确界为12；通常情况下，迭代总次数为$n = \left\lceil {{\rm{lo}}{{\rm{g}}_2}{\rm{di}}{{\rm{s}}_B}} \right\rceil + \left\lceil {{\rm{lo}}{{\rm{g}}_2}{\rm{di}}{{\rm{s}}_{R'}}} \right\rceil $. 它也证明改进减法直方图算法是收敛的.

3) 改进减法直方图加速算法改进了文献[9] iSH加速算法收敛速度对先验知识的依赖，成为更先进的不需要任何先验知识的自适应算法.

4) 通过重构α'特征，相关算法对比和直方图单峰检测实验，结果显示：算法是有效的.

本文20组实验土壤图像样本中，最小的阴影占比为2.386%，本文算法对低于此阴影占比土壤图像阴影检测的适应性尚需进一步实验验证，对低阴影占比土壤图像阴影检测可能尚需要进一步研究.