在这篇文章中，我们将研究下列含有马尔可夫跳的二维罗塞尔(Roesser)模型：

其中：

x^h(i，j)∈$\mathbb{R}^{{n}_h}$表示在水平方向的状态，同理，x^v(i，j)∈$\mathbb{R}^{{n}_v}$表示在垂直方向的状态，u(i, j)∈$\mathbb{R}$^n_u表示控制输入，ω(i, j)∈$\mathbb{R}$^n_ω表示扰动输入，y(i, j)∈$\mathbb{R}$^n_y表示输出，z(i, j)∈$\mathbb{R}$^n_z表示控制输出. A(γ_{i, j})，B(γ_{i, j})，C(γ_{i, j})，E(γ_{i, j})，F(γ_{i, j})，G₁(γ_{i, j})，G₂(γ_{i, j})，G₃(γ_{i, j})，G₄(γ_{i, j})都是已知的相应维数的实值矩阵，它们都是γ_{i, j}的函数，γ_{i, j}是马尔可夫链. γ_{i, j}∈H₁={1，2，…，k₁}并且具有转移函数矩阵Λ=(λ_pq)，

这里的δ＞0并且γ_{i, j}≥0是从i到j的转移率.

注1  本文研究的系统是带有马尔可夫跳的. 不带马尔可夫跳的情形，能够作为本文的一个极其特殊的情况.

根据现代概率理论，对∀p，q∈H₁有

系统的边界条件(X₀，Γ₀)被定义为

定义零边界条件：x^h(0，j)=0，x^v(i，0)=0，i, j=0，1，2，…. 下面对X₀进行假设.

假设1  假设X₀满足下列条件，

这里的E(·)表示数学期望，|·|表示欧基米德范数.

假设γ_{i, j}的准确数值是难以获得的. 若(1)式中F(γ_{i, j})为空矩阵，B₁(γ_{i, j})为列满秩的矩阵，本文将设计如下异步输出反馈控制器：

其中：A_c，11(η_{i, j})，A_c，12(η_{i, j})，A_c，21(η_{i, j})，A_c，22(η_{i, j})，B_c，1(η_{i, j})，B_c，2(η_{i, j})，C_c，1(η_{i, j})，C_c，2(η_{i, j})，K(η_{i, j})都表示表示控制增益，其中η_{i, j}是决定控制增益的参数，η_{i, j}∈H₂，H₂={1，2，…，k₂}. 同时由γ_{i, j}得到条件概率π_ps，即

本文利用蒙特卡洛方法得到条件概率矩阵Π=(π_ps)且满足条件

1) π_ps∈[0, 1]，

2) $\sum\limits_{s=1}^{k_{2}}$π_ps=1.

对任意的p∈H₁，s∈H₂.

为了方便计算，分别用p，q，s表示γ_{i, j}，γ_i+1，j(γ_{i, j+1})和η_{i, j}，即A_p表示A(γ_{i, j}).

将(6)式代入(1)式，得到下面的闭环动力系统：

这里的

下面根据一维系统的耗散性给出带有马尔科夫跳的二维罗塞尔系统的严格的2D(Q，S，R)-α耗散性定义和系统渐近稳定性.

定义1  ^[20]对二维闭环系统ξ，输入ω(i, j)≡0若对任意边界条件(X₀，Γ₀)满足

则称二维闭环系统ξ是渐近均方稳定的.

定义2  ^[20]假设二维闭环系统ξ满足假设1，如果在零边界条件和ω(i, j)∈l₂{[0，∞)，[0，∞)}下，下列条件成立

Q，S和R是对称矩阵，其中α＞0，Q =-Q_*^TQ_*≤0，则ξ是严格2D(Q，S，R)-α耗散.

注2  (10)式是由Willems所提出的耗散不等式.

本文将设计一个形如(6)式的异步控制器来保证二维罗塞尔系统ξ的渐近稳定性和2D(Q，S，R)-α耗散性能.

本节将研究对于带有马尔科夫跳的二维罗塞尔系统ξ的渐近均方稳定性和严格的2D(Q，S，R)-α耗散并提出控制器的设计方法. 首先给出一个充分条件：

定理1  在假设1的条件下思考闭环二维系统ξ，对给定的α＞0以及对称矩阵Q和R，其中

如果存在一个对称矩阵R_p=diag{R_p^h，R_p^v}＞0，Q_ps＞0和K_s，对于∀p∈H₁，s∈H₂，下列条件成立：

其中

则系统ξ是渐近均方稳定的和严格2D(Q，S，R)-α耗散的

证  首先定义一个新的矩阵Λ：

将矩阵(12)前乘Λ，后乘Λ^T，那么矩阵(12)转换为下列矩阵

基于舒尔补定理，下列线性矩阵不等式与矩阵(14)是等价的：

1) 当-R_p^-1＜0时，有φ₁=-Q_ps+A_ps^TR_pA_ps＜0.

2) 当$\left[\begin{array}{cc}-\overline{\boldsymbol{R}}_{p}^{-1} & 0 \\ 0 & -\boldsymbol{I}\end{array}\right] < 0$时，有

下面将从系统的渐近均方稳定性进行证明. 假设ω(i, j)≡0，定义Lyapunov函数V(i, j)=$\tilde{\boldsymbol{x}}$^T(i, j)·R_q$\tilde{\boldsymbol{x}}$(i, j)，那么

根据假设ω(i, j)≡0，系统可变为x¹(i, j)=A_psx(i, j)，所以

对ΔV(i, j)求期望得

基于φ₁得

将(18)式带入(17)式得

其中φ=λ_min(R_p-$\sum\limits_{s=1}^{k_{2}}$π_psQ_ps)是最小的特征值. 由(11)式知R_p-$\sum\limits_{s=1}^{k_{2}}$π_psQ_ps＞0，所以φ＞0.

根据(19)式得到

另一方面，

这里的m，n是任意的正整数. 因为R_p=diag{R_p^h，R_p^v}＞0，所以根据(20)式得到

下面让m和n趋于无穷大，

这里的σ=λ_max{R^h_γ0，j，R^v_γi，0}，而根据假设1，得到

这表示(9)式成立，所以系统ξ是渐近均方稳定的.

下面证明在零边界条件下系统ξ的耗散性. 定义Ω=[$\tilde{\boldsymbol{x}}$^T(i, j)，ω^T(i, j)]^T，首先对矩阵(12)进行处理，让其前乘N^T后乘N

根据舒尔补定理，矩阵(12)的期望等价于

这里的

下面定义J，由(11)式和(26)式得到

这里的

注意到

在零边界条件下结合(27)，(28)式有

根据定义2系统ξ是严格的2D(Q，S，R)-α耗散. 定理得证.

注3  矩阵Q_ps可以使包含控制器增益K_s的矩阵A_ps和C_ps与π_ps成功分离，减少矩阵不等式的维数，降低控制器的复杂度.

注4  通过选择Q=0，S=I和R=2αI，得到系统ξ是无源性的条件，即满足

注5  通过选择Q =-I，S = 0和R =(α²+α) I，得到了系统ξ是H_∞性的条件，即满足

虽然定理1给出了一个形式简单的充分条件，但由于非线性的存在，将其直接用于控制器设计是困难的. 接下来进一步研究控制器的设计方法.

定理2  假定系统(1)中F是空矩阵，B是列满秩矩阵，给定一个标量α＞0和3个矩阵Q，S和R，其中Q和S是实对称矩阵，对于一些Q_*，这里的Q=-Q_*^TQ_*≤0. 那么闭环系统ξ是均方渐近稳定的并且是2D(Q，S，R)-α耗散. 如果存在矩阵L₁，两个正定矩阵M₁M₂，一个正定的对角矩阵R_p=diag{R_p^h，R_p^v}＞0，这里的R_p^h=R_p^hT＞0和R_p^v=R_p^vT＞0，使(11)式成立且

这里的

并且T是一个可逆的转移矩阵满足TΞA=$\left[\begin{array}{l}\boldsymbol{I} \\ 0\end{array}\right]$，则控制器增益Θ_c=S₁^-1L₁.

证  定义M=T^TMT，根据上述，得到

将(30)式前乘diag{T^T，I，I，I }后乘diag{ T，I，I，I}，并且根据M=T^TMT得到

然后将(33)式前乘diag{M^-1，I，I，I }和后乘diag{M^-T，I，I，I}.

由于不等式(M^-1-P^-1)R_p(M^-1-P^-1)^T≥0，得到R_p^-1≥ M^-1+ M^-T-M^-1R_pM^-T，则(32)式能够保证下列不等式成立：

这里的

然后将(33)式前乘diag{R_p，I，I，I }后乘diag{R_p，I，I，I}，则得到定理1中的(14)式，运用定理1，得到系统ξ是均方稳定的和2D(Q，S，R)-α耗散的，证明完成.

注6  定理2通过松弛矩阵技术和变量替换处理矩阵不等式(11)和(12)所涉及的非线性问题，成功地将控制设计问题转化为一个基于LMI的问题，利用Matlab可以轻松地解决该问题.

本节将使用Darboux方程来验证控制器的有效性. 这里选择以下的马尔可夫跳跃系统，相应的系统矩阵如下所示：

由马尔可夫跳跃组成的系统矩阵满足以下转移概率矩阵和条件概率矩阵：

然后利用定理2中提出的控制器设计方法得到如下控制器增益：

接下来，将通过比较有控制输入和无控制输入时系统状态的演化来进一步证明其有效性. 因此，有必要提出边界条件：

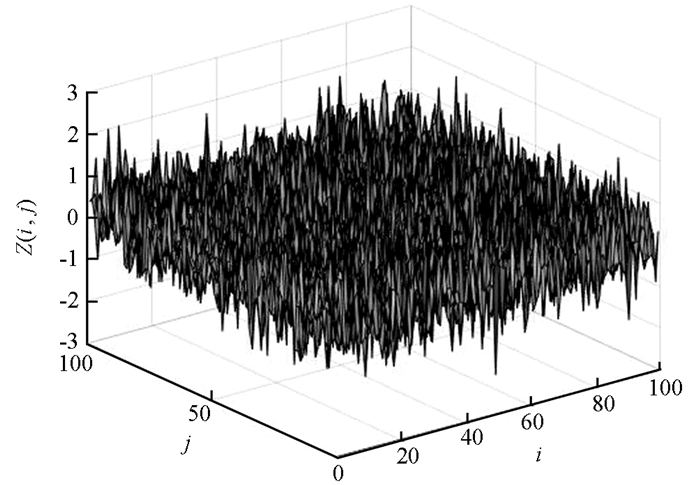
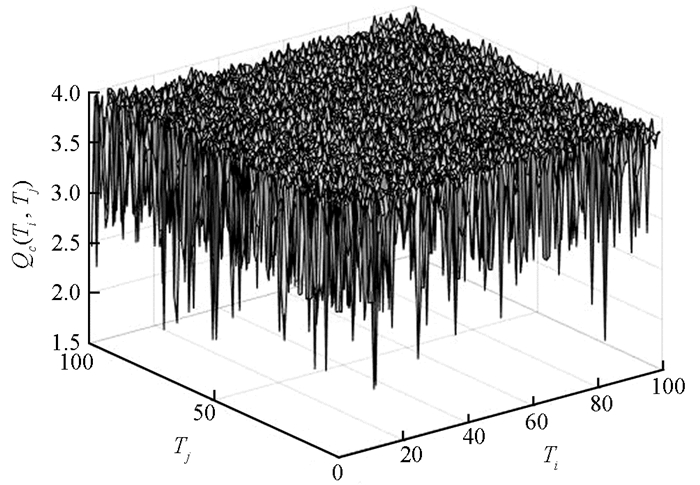
而w(i, j)是满足正态分布的随机数，根据这些零边界条件和系数条件可以得到不带有控制输出的开环系统. 选择Q=-1，S=1，R=3，得到Q_c(T_i，T_j)(图 1)与随机场状态z(i, j)(图 2). 从图 1可知参数α的最小值，即α=1.927 1. 图 2可知控制器能有效地稳定开环系统.

本文研究了基于罗塞尔模型构建的二维马尔可夫系统的2D(Q，S，R)-α耗散控制问题. 考虑到系统模式信息的不可获取性，我们将研究重点放在了异步控制上，建立了被控二维系统与控制器之间异步的隐马尔可夫模型. 将一维系统的耗散性定义推广到二维系统，得到了保证系统渐近均方稳定性和2D(Q，S，R)-α耗散的充分条件，并且通过优化技术给出了一种控制器的设计方法. 在之后的工作中，将考虑在有限域上开展异步控制器的设计及其有效性论证的工作.